


山西省(临汾地区)2022-2023学年数学七年级第二学期期末检测试题含答案
展开山西省(临汾地区)2022-2023学年数学七年级第二学期期末检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.货车行驶 25 千米与小车行驶 35 千米所用时间相同,已知小车每小时比货车多行驶 20千米,求两车的速度各为多少?设货车的速度为 x 千米/小时,依题意列方程正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知一元二次方程x2-2x-m=0有两个实数根,那么m的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.乒乓球是我国的国球,也是世界上流行的球类体育项目.我国乒乓球名将与其对应身高如下表所示:
乒乓球名将 | 刘诗雯 | 邓亚萍 | 白杨 | 丁宁 | 陈梦 | 孙颖莎 | 姚彦 |
身高( | 160 | 155 | 171 | 173 | 163 | 160 | 175 |
这些乒乓球名将身高的中位数和众数是( )
A.160,163 B.173,175 C.163,160 D.172,160
4.如图,在△ABC中,若AB=AC=6,BC=4,D是BC的中点,则AD的长等于( )
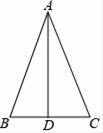
A.4![]() B.2
B.2![]() C.2
C.2![]() D.4
D.4
5.五一小长假,李军与张明相约去宁波旅游,李军从温岭北上沿海高速,同时张明从玉环芦浦上沿海高速,温岭北与玉环芦浦相距44千米,两人约好在三门服务区集合,李军由于离三门近,行驶了1.2小时先到达三门服务站等候张明,张明走了1.4小时到达三门服务站。在整个过程中,两人均保持各自的速度匀速行驶,两人相距的路程y千米与张明行驶的时间x小时的关系如图所示,下列说法错误的是( )
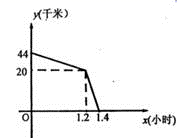
A.李军的速度是80千米/小时
B.张明的速度是100千米/小时
C.玉环芦浦至三门服务站的路程是140千米
D.温岭北至三门服务站的路程是44千米
6.下列各式正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.把多项式![]() 分解因式,下列结果正确的是( )
分解因式,下列结果正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若代数式![]() 有意义,则一次函数
有意义,则一次函数![]() 的图象可能是
的图象可能是
A.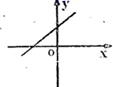 B.
B.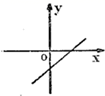 C.
C.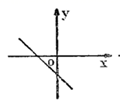 D.
D.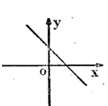
9.某玩具厂要生产a只吉祥物“欢欢”,原计划每天生产b只,实际每天生产了(b+c)只,则该厂提前完成任务的天数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积之和为( )
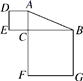
A.150 B.200 C.225 D.无法计算
11.一次信息技术模拟测试后,数学兴趣小组的同学随机统计了九年级20名学生的成绩![]() 记录如下:有5人得10分,6人得9分,5人得8分,4人得7分
记录如下:有5人得10分,6人得9分,5人得8分,4人得7分![]() 这20名学生成绩的中位数和众数分别是
这20名学生成绩的中位数和众数分别是![]()
![]()
A.10分,9分 B.9分,10分 C.9分,9分 D.![]() 分,9分
分,9分
12.使等式![]() 成立的x的值是( )
成立的x的值是( )
A.是正数 B.是负数 C.是0 D.不能确定
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.菱形![]() 的两条对角线相交于
的两条对角线相交于![]() ,若
,若![]() ,
,![]() ,则菱形
,则菱形![]() 的周长是___.
的周长是___.
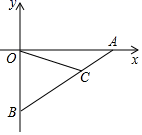
14.一个n边形的每一个内角等于108°,那么n=_____.
15.在平面直角坐标系中点![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点且
轴上的点且![]() 点的坐标是
点的坐标是![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,是靠近点
上,是靠近点![]() 的三等分点.点
的三等分点.点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标是__________.
的坐标是__________.
16.方程![]() =2的解是_________
=2的解是_________
17.函数![]() 中,若自变量
中,若自变量![]() 的取值范围是
的取值范围是![]() ,则函数值
,则函数值![]() 的取值范围为__________.
的取值范围为__________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)已知直线y=kx+b经过点A(0,1),B(2,5).
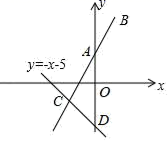
(1)求直线AB的解析式;
(2)若直线y=﹣x﹣5与直线AB相交于点C.求点C的坐标;并根据图象,直接写出关于x的不等式﹣x﹣5<kx+b的解集.
(3)直线y=﹣x﹣5与y轴交于点D,求△ACD的面积.
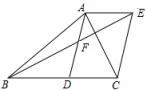
19.(5分)如图,![]() 是
是![]() 的中线,
的中线,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 的面积为
的面积为![]() ,请直接写出图中所有面积是
,请直接写出图中所有面积是![]() 的三角形.
的三角形.
20.(8分)某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题对全校学生进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
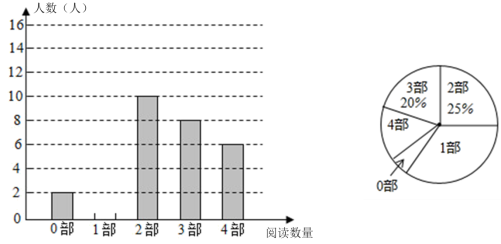
(1)请将条形统计图补充完整,本次调查所得数据的众数是_______,中位数是________;
(2)请通过计算估计全校学生平均每人大约阅读多少部四大古典名著.
21.(10分)某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘新工人若干名(新工人人数少于10人)和抽调的熟练工合作,刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
22.(10分)某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:
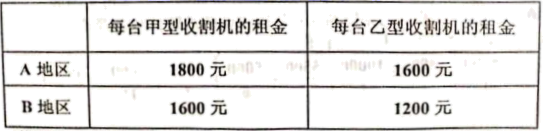
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机天获得的租金为y元,求y关于x的函数关系式,并写出自变量的取值范围:
(2)若使农机租赁公司这50台收割机一天所获租金不低于79600元,为农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.
23.(12分)先化简,再求值:![]() ,其中x=1.
,其中x=1.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、B
3、C
4、A
5、D
6、D
7、A
8、A
9、D
10、C
11、C
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、1
15、(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2)
)或(0,-2)
16、![]()
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)直线AB的解析式为y=2x+1;(2)x>﹣2;(3)△ACD的面积为1.
19、(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]()
20、(1)图见解析,1部,2部;(2)2部
21、(1)每名熟练工每月可以安装4辆电动车,新工人每月分别安装2辆电动汽车.
(2) ①调熟练工1人,新工人8人;②调熟练工2人,新工人6人;③调熟练工3人,新工人4人;④调熟练工4人,新工人2人.
22、(1)y=200x+74000(10≤x≤30);(2)将30台乙型收割机全部派往A地区,20台甲型收割机全部派往B地区,这样公司每天获得租金最高,理由见解析.
23、![]() ,-1
,-1
山西省(临汾地区)2023-2024学年数学九上期末教学质量检测试题含答案: 这是一份山西省(临汾地区)2023-2024学年数学九上期末教学质量检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
山西省(临汾地区)2023-2024学年九上数学期末质量检测模拟试题含答案: 这是一份山西省(临汾地区)2023-2024学年九上数学期末质量检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,在单词prbability,已知在直角坐标平面内,以点P等内容,欢迎下载使用。
山西省(临汾地区)2023-2024学年数学八上期末达标检测模拟试题含答案: 这是一份山西省(临汾地区)2023-2024学年数学八上期末达标检测模拟试题含答案,共7页。试卷主要包含了下列命题中是真命题的是,估计的值应在等内容,欢迎下载使用。












