


山东省泰安市泰山区大津口中学2022-2023学年七下数学期末统考试题含答案
展开山东省泰安市泰山区大津口中学2022-2023学年七下数学期末统考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,函数![]() 与
与![]() ,在同一坐标系中的大致图像是()
,在同一坐标系中的大致图像是()
A.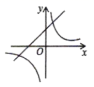 B.
B.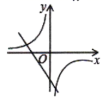
C.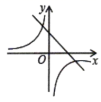 D.
D.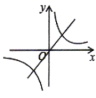
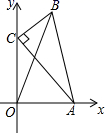
2.如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动.在运动过程中,点B到原点的最大距离是( )
A.6 B.2![]() C.2
C.2![]() D.2
D.2![]() +2
+2
3.如果一组数据为1,5,2,6,2,则这组数据的中位数为( )
A.6 B.5 C.2 D.1
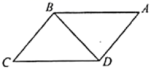
4.如图,在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.某学习小组7位同学,为玉树地重灾区捐款,捐款金额分别为:5元,10元,6元,6元,7元,8元,9元,则这组数据的中位数与众数分别为( )
A.6,6 B.7,6 C.7,8 D.6,8
6.已知点P(a+l,2a-3)关于x轴的对称点在第一象限,则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在平行四边形![]() 中,下列结论一定成立的是( )
中,下列结论一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
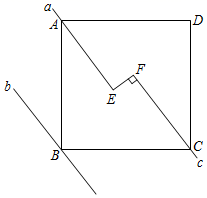
9.如图,已知正方形ABCD的面积等于25,直线a,b,c分别过A,B,C三点,且a∥b∥c,EF⊥直线c,垂足为点F交直线a于点E,若直线a,b之间的距离为3,则EF=( )
A.1 B.2 C.![]() -3 D.5-
-3 D.5-![]()
10.如果把分式![]() 中的x和y都扩大3倍,那么分式的值( )
中的x和y都扩大3倍,那么分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.无法确定
11.若![]() ,则下列各不等式不一定成立的是( )
,则下列各不等式不一定成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.下列各因式分解的结果正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.若对于![]() 的任何值,等式
的任何值,等式![]() 恒成立,则
恒成立,则![]() __________.
__________.
14.最简二次根式![]() 与
与![]() 是同类二次根式,则
是同类二次根式,则![]() =______.
=______.
15.某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物指数如表,则该周PM2.5指数的众数和中位数分别是________
PM2.5指数 | 150 | 155 | 160 | 165 |
天 数 | 3 | 2 | 1 | 1 |
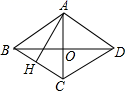
16.如图,在菱形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,已知BO=4,S菱形ABCD=24,则
,已知BO=4,S菱形ABCD=24,则![]() ___.
___.
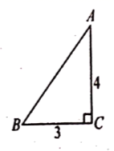
17.如图,一张三角形纸片![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,现小林将纸片做三次折叠:第一次使点
,现小林将纸片做三次折叠:第一次使点![]() 落在
落在![]() 处;将纸片展平做第二次折叠,使点
处;将纸片展平做第二次折叠,使点![]() 若在
若在![]() 处;再将纸片展平做第三次折叠,使点
处;再将纸片展平做第三次折叠,使点![]() 落在
落在![]() 处,这三次折叠的折痕长依次记为
处,这三次折叠的折痕长依次记为![]() ,则
,则![]() 的大小关系是(从大到小)__________.
的大小关系是(从大到小)__________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸到球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计当![]() 很大时,摸到白球的频率将会接近______;(精确到0.1);
很大时,摸到白球的频率将会接近______;(精确到0.1);
(2)假如随机摸一次,摸到白球的概率P(白球)=______;
(3)试估算盒子里白色的球有多少个?
19.(5分)如图,在矩形![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.
上.
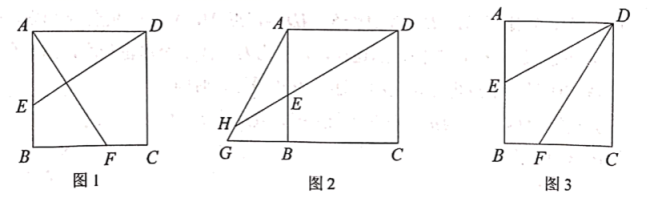
(1)若![]() ,
,![]() .
.
①如图1,求证:![]() ;
;
②如图2,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 的延长线交
的延长线交![]() 于
于![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(2)如图3,若![]() 为
为![]() 的中点,
的中点,![]() .则
.则![]() 的值为 (结果用含
的值为 (结果用含![]() 的式子表示)
的式子表示)
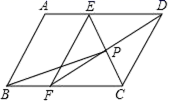
20.(8分)如图,在▱ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.
(1)求证:四边形CDEF是菱形;
(2)若AB=2,BC=3,∠A=120°,求BP的值.
21.(10分)为了了解某公司员工的年收入情况,随机抽查了公司部分员工年收入情况并绘制如图所示统计图.
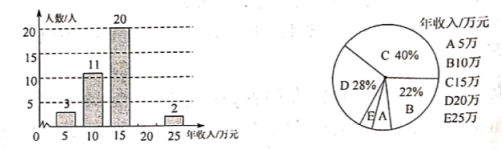
(1)请按图中数据补全条形图;
(2)由图可知员工年收入的中位数是 ,众数是 ;
(3)估计该公司员工人均年收入约为多少元?
22.(10分)化简求值: 1(![]() +1)(
+1)(![]() -1)-
-1)-![]() (1
(1![]() -1),其中
-1),其中![]() =1.
=1.
23.(12分)计算.
(1)![]()
(2)![]()
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
2、D
3、C
4、B
5、B
6、B
7、D
8、B
9、A
10、A
11、D
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、4
15、150,1
16、![]()
17、b>c>a.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)0.1;(2)0.1;(3)30个
19、(1)①见解析;②见解析;(2)![]()
20、 (1)证明见解析;(2)BP的值为![]() .
.
21、(1) 见解析;(2)15,15;(3)人均年收入为15.1万元.
22、![]() ;0
;0
23、(1)![]() ;(2)
;(2)![]() .
.
山东省泰安市泰山区大津口中学2023-2024学年数学九年级第一学期期末经典模拟试题含答案: 这是一份山东省泰安市泰山区大津口中学2023-2024学年数学九年级第一学期期末经典模拟试题含答案,共7页。
2023-2024学年山东省泰安市大津口中学九上数学期末经典模拟试题含答案: 这是一份2023-2024学年山东省泰安市大津口中学九上数学期末经典模拟试题含答案,共8页。
山东省泰安市泰山区大津口中学2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案: 这是一份山东省泰安市泰山区大津口中学2023-2024学年八年级数学第一学期期末教学质量检测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,已知,-9的立方根为等内容,欢迎下载使用。












