


安徽省颍上六十铺中学2022-2023学年数学七下期末联考试题含答案
展开安徽省颍上六十铺中学2022-2023学年数学七下期末联考试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.若代数式![]() 有意义,则一次函数
有意义,则一次函数![]() 的图象可能是
的图象可能是
A.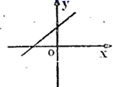 B.
B.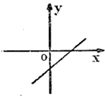 C.
C.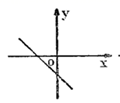 D.
D.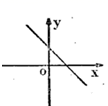
2.如图,把一个边长为1的正方形放在数轴E,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数为( ).
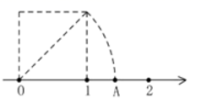
A.2 B.1.4 C.3 D.1.7
3.△ABC中,AB=13,AC=15,高AD=12,则BC的长为( )
A.14 B.4 C.14或4 D.以上都不对
4.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为
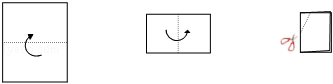
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
5.10名学生的平均成绩是x,如果另外5名学生每人得90分,那么整个组的平均成绩是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.▱ABCD中,如果![]() ,那么
,那么![]() 、
、![]() 的值分别是
的值分别是![]()
![]()
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
7.![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.如图,在正方形![]() 中,
中,![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠至
折叠至![]() 处,
处, ![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,则
,则![]() 的大小为( )
的大小为( )
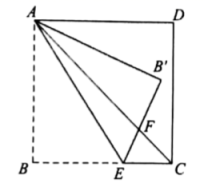
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.下列从左边到右边的变形,是因式分解的是![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.一次跳远比赛中,成绩在4.05米以上的有8人,频率为0.4,则参加比赛的共有( )
A.40人 B.30人 C.20人 D.10人
二、填空题(本大题共有6小题,每小题3分,共18分)
11.一般地,在平面直角坐标系中,我们求点到直线间的距离,可用下面的公式求解:
点![]() 到直线
到直线![]() 的距离
的距离![]() 公式是:
公式是:![]()
如:求:点![]() 到直线
到直线![]() 的距离.
的距离.
解:由点到直线的距离公式,得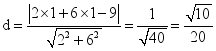
根据平行线的性质,我们利用点到直线的距离公式,也可以求两平行线间的距离.
则两条平行线![]() :
:![]() 和
和![]() :
:![]() 间的距离是______.
间的距离是______.
12.与向量![]() 相等的向量是__________.
相等的向量是__________.
13.小刚和小丽从家到运动场的路程都是![]() ,其中小丽走的是平路,骑车速度是
,其中小丽走的是平路,骑车速度是![]()
![]() .小刚需要走
.小刚需要走![]() 上坡路和
上坡路和![]() 的下坡路,在上坡路上的骑车速度是
的下坡路,在上坡路上的骑车速度是![]()
![]() ,在下坡路上的骑车速度是
,在下坡路上的骑车速度是![]()
![]() .如果他们同时出发,那么早到的人比晚到的人少用_________
.如果他们同时出发,那么早到的人比晚到的人少用_________![]() .(结果化为最简)
.(结果化为最简)
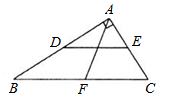
14.如图,在Rt△ABC中,已知∠BAC=90°,点D、E、F分别是三边的中点,若AF=3cm,则DE=_____cm.
15.已知菱形两条对角线的长分别为4和6,则菱形的边长为______.
16.对于一次函数![]() ,若
,若![]() ,那么
,那么![]() 对应的函数值y1与y2的大小关系是________.
对应的函数值y1与y2的大小关系是________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到永丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,![]() ,
,![]() .
.
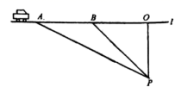
(1)求A、B之间的路程;
(2)请判断此车是否超过了永丰路每小时54千米的限制速度?(参考数据:![]() )
)
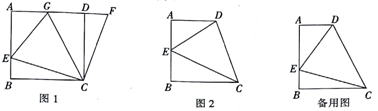
18.(8分)如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗;为什么;
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
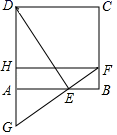
19.(8分)如图,已知正方形ABCD的边长是2,点E是AB边上一动点(点E与点A、B不重合),过点E作FG⊥DE交BC边于点F、交DA的延长线于点G,且FH∥AB.
(1)当DE=![]() 时,求AE的长;
时,求AE的长;
(2)求证:DE=GF;
(3)连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数关系式.
20.(8分)(1)计算: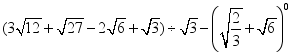 ;
;
(2)已知x=2−![]() ,求(7+4
,求(7+4![]() )x2+(2+
)x2+(2+![]() )x+
)x+![]() 的值
的值
21.(8分)已知直线l为x+y=8,点P(x,y)在l上且x>0,y>0,点A的坐标为(6,0).
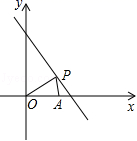
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
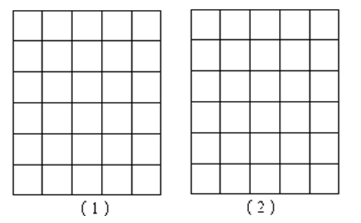
22.(10分)如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.
(1)使三角形三边长为3,![]() ,
,![]() ;
;
(2)使平行四边形有一锐角为15°,且面积为1.
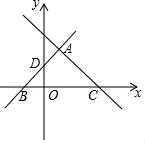
23.(10分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点C与直线AD交于点A(1,2),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,请判断△ABC的形状;
(3)在直线AD上是否存在一点E,使得4S△BOD=S△ACE,若存在求出点E的坐标,若不存在说明理由.
24.(12分)平面直角坐标系中,直线y=2kx-2k (k>0)交y轴于点B,与直线y=kx交于点A.
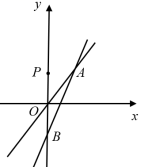
(1)求点A的横坐标;
(2)直接写出![]() 的x的取值范围;
的x的取值范围;
(3)若P(0,3)求PA+OA的最小值,并求此时k的值;
(4)若C(0,2)以A,B,C,D为顶点的四边形是以BC为一条边的菱形,求k的值.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、C
4、D
5、D
6、B
7、C
8、B
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、![]()
14、3
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)A、B之间的路程为73米;(2)此车超过了永丰路的限制速度.
18、(1)证明见解析;(2)成立;(3)①12;②7.1
19、(1)![]() ;(2)见解析;(3)y=
;(2)见解析;(3)y=![]() (0<x<2).
(0<x<2).
20、(1)9-2![]() ;(2)2+
;(2)2+![]()
21、(1)、y=24﹣3x(0<x<8);(2)、P(5,3);(3)、(6.4,1.6).
22、(1)详见解析;(2)详见解析
23、 (1)y=x+1;(2)△ABC是等腰直角三角形;(3)存在,点E的坐标为(2,3)或(0,1)时,4S△BOD=S△ACE.
24、(1)![]() 点横坐标为2;(2)
点横坐标为2;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 或
或![]() .
.
2023-2024学年安徽省颍上六十铺中学八上数学期末综合测试模拟试题含答案: 这是一份2023-2024学年安徽省颍上六十铺中学八上数学期末综合测试模拟试题含答案,共8页。试卷主要包含了估算的值在,9的平方根是,下列命题是假命题的是等内容,欢迎下载使用。
阜阳颍南中学2022-2023学年七下数学期末检测试题含答案: 这是一份阜阳颍南中学2022-2023学年七下数学期末检测试题含答案,共7页。试卷主要包含了下列根式中是最简二次根式的是,下列事件中,属于随机事件的是等内容,欢迎下载使用。
安徽省阜阳颍东区四校联考2022-2023学年数学七下期末经典试题含答案: 这是一份安徽省阜阳颍东区四校联考2022-2023学年数学七下期末经典试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列各式属于最简二次根式的有等内容,欢迎下载使用。












