


宁夏省重点中学2022-2023学年七年级数学第二学期期末达标检测试题含答案
展开宁夏省重点中学2022-2023学年七年级数学第二学期期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
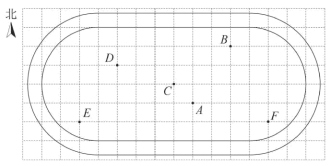
1.为了保障艺术节表演的整体效果,某校在操场中标记了几个关键位置,如图是利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为![]() ,表示点B的坐标为
,表示点B的坐标为![]() ,则表示其他位置的点的坐标正确的是( )
,则表示其他位置的点的坐标正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,在平行四边形ABCD中,点A1, A2, A3, A4和C1, C2, C3, C4分别是AB和CD的五等分点,点B1, B2和D1,D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为18,则平行四边形ABCD的面积为( )
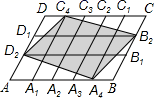
A.22 B.25 C.30 D.15
3.若分式![]() 有意义,则x应满足的条件是( )
有意义,则x应满足的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A.点(0,k)在l上
B.l经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.l经过第一、二、三象限
5.用反证法证明“三角形中至少有一个内角大于或等于![]() ”时,应假设( )
”时,应假设( )
A.三角形的二个内角小于![]() B.三角形的三个内角都小于
B.三角形的三个内角都小于![]()
C.三角形的二个内角大于![]() D.三角形的三个内角都大于
D.三角形的三个内角都大于![]()
6.某校组织数学学科竞赛为参加区级比赛做选手选拔工作,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表,如果从这四位同学中选出一名晋级(总体水平高且状态稳定)你会推荐( )
| 甲 | 乙 | 丙 | 丁 |
平均分 | 92 | 94 | 94 | 92 |
方差 | 35 | 35 | 23 | 23 |
A.甲 B.乙 C.丙 D.丁
7.根据图1所示的程序,得到了如图y与x的函数图像,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图像于点P、Q,连接OP、OQ.则以下结论:①x<0 时,y=![]() ;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM⑤∠POQ可以等于90°.其中正确结论序号是( )
;②△OPQ的面积为定值;③x>0时,y随x的增大而增大;④MQ=2PM⑤∠POQ可以等于90°.其中正确结论序号是( )
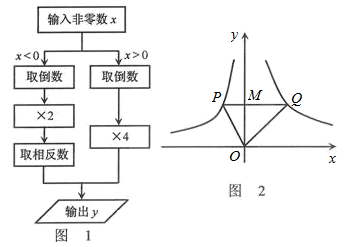
A.①②③ B.②③④ C.③④⑤ D.②④⑤
8.将直线y=-2x-3怎样平移可以得到直线y=-2x的是( )
A.向上平移2个单位 B.向上平移3个单位
C.向下平移2个单位 D.向下平移3个单位
9.若![]() 与最简二次根式
与最简二次根式![]() 是同类二次根式,则m的值为( )
是同类二次根式,则m的值为( )
A.7 B.11 C.2 D.1
10.一元二次方程x2-9=0的解为( )
A.x1=x2=3 B.x1=x2=-3 C.x1=3,x2=-3 D.x1=![]() ,x2=-
,x2=-![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.将直线y=2x+1向下平移3个单位长度后所得直线的表达式是 ______.
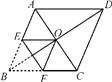
12.如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
13.一个n边形的每一个内角等于108°,那么n=_____.
14.直线![]() 与两坐标轴围成的三角形的面积为4,则
与两坐标轴围成的三角形的面积为4,则![]() 的值为______.
的值为______.
15.已知关于![]() 的方程
的方程![]() 会产生增根,则
会产生增根,则![]() 的值为________.
的值为________.
16.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2![]() ,那么△DEF的周长是_____.
,那么△DEF的周长是_____.
三、解下列各题(本大题共8小题,共72分)
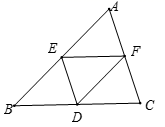
17.(8分)如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF.
BC,连结DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.
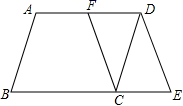
18.(8分)问题发现:
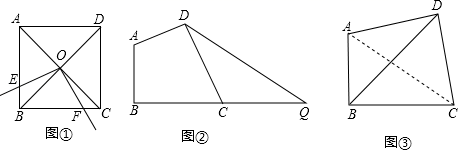
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
19.(8分)已知![]() 为原点,点
为原点,点![]() 及在第一象限的动点
及在第一象限的动点![]() ,且
,且![]() ,设
,设![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 点坐标;
点坐标;
(4)画出函数![]() 的图象.
的图象.
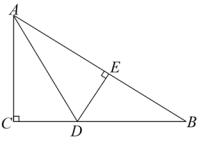
20.(8分)如图,在Rt△ABC中,∠C=90°,E是AB上的点,且AE=AC,DE⊥AB交BC于D,AC=6,BC=8,CD=1.
(1)求DE的长;
(2)求△ADB的面积.
21.(8分)如图,在网格图中,平移![]() 使点
使点![]() 平移到点
平移到点![]() ,每小格代表1个单位。
,每小格代表1个单位。
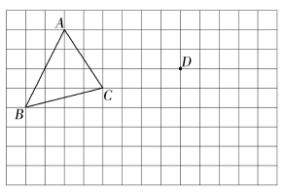
(1)画出平移后的![]() ;
;
(2)求![]() 的面积.
的面积.
22.(10分)如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 的坐标为
的坐标为![]() .
.
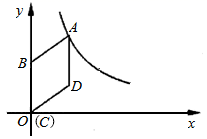
(1)求![]() 的值.
的值.
(2)将点![]() 沿
沿![]() 轴正方向平移得到点
轴正方向平移得到点![]() ,当点
,当点![]() 在函数
在函数![]() 的图象上时,求
的图象上时,求![]() 的长.
的长.
23.(10分)已知王亮家、公园、新华书店在一条直线上,下面的图象反映的过程是:王亮从家跑步去公园,在那里锻炼了一阵后又走到新华书店去买书,然后散步走回家.其中![]() 表示时间,
表示时间,![]() 表示王亮离家的距离.
表示王亮离家的距离.
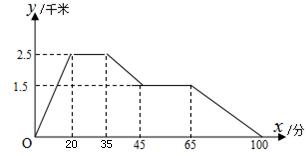
根据图象回答:
(1)公园离王亮家 ![]() ,王亮从家到公园用了
,王亮从家到公园用了 ![]() ;
;
(2)公园离新华书店 ![]() ;
;
(3)王亮在新华书店逗留了 ![]() ;
;
(4)王亮从新华书店回家的平均速度是多少?
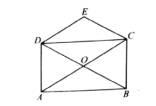
24.(12分)如图,O是矩形ABCD对角线的交点,作![]() ,
,![]() ,DE,CE相交于点E,求证:四边形OCED是菱形.
,DE,CE相交于点E,求证:四边形OCED是菱形.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、A
4、D
5、B
6、C
7、D
8、B
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、y=1x-1
12、2
13、1
14、![]()
15、1
16、10+![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析(2)![]()
18、(1)4;(2)5![]() ;(3)600(
;(3)600(![]() +1).
+1).
19、(1)S=−4x+48;(2)0<x<12;(3)P(1,3);(4)见解析.
20、(1)1;(2)15
21、(1)详见解析;(2)![]()
22、 (1)k=12;(2)DD′=![]() .
.
23、(2)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
24、见解析
湘潭市重点中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案: 这是一份湘潭市重点中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,函数中,自变量的取值范围是等内容,欢迎下载使用。
温州市重点中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案: 这是一份温州市重点中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共6页。
宁夏省石嘴山市2022-2023学年数学七下期末达标检测试题含答案: 这是一份宁夏省石嘴山市2022-2023学年数学七下期末达标检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列各式计算正确的是等内容,欢迎下载使用。












