


安徽省当涂县2022-2023学年七下数学期末达标检测模拟试题含答案
展开这是一份安徽省当涂县2022-2023学年七下数学期末达标检测模拟试题含答案,共7页。试卷主要包含了若分式有意义,则x的取值范围是等内容,欢迎下载使用。
安徽省当涂县2022-2023学年七下数学期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.在 2008 年的一次抗震救灾大型募捐活动中,文艺工作者积极向灾区捐款.其中 10 人 的捐款分别是:5 万,8 万,10 万,10 万,10 万,20 万,20 万,30 万,50 万,100 万.这组数据的众数和中位数分别是( )
A.10 万,15 万 B.10 万,20 万 C.20 万,15 万 D.20 万,10 万
2.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的周长是( )
的周长是( )
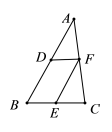
A.5 B.7 C.9 D.11
3.下列条件:
①两组对边分别平行
②两组对边分别相等
③两组对角分别相等
④两条对角线互相平分
其中,能判定四边形是平行四边形的条件的个数是( )
A.1 B.2 C.3 D.4
4.如果实数![]() 满足
满足![]() 且不等式
且不等式![]() 的解集是
的解集是![]() ,那么函数
,那么函数![]() 的图象只可能是( )
的图象只可能是( )
A.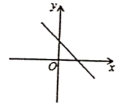 B.
B.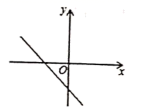 C.
C.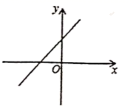 D.
D.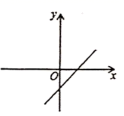
5.如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点E在BC边上可移动的最大距离为( )
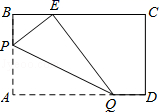
A.1 B.2 C.4 D.5
6.已知y=(k−3)x![]() +2是一次函数,那么k的值为( )
+2是一次函数,那么k的值为( )
A.±3 B.3 C.−3 D.±1
7.若分式![]() 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A.x=1 B.x≠1 C.x>1 D.x<1
8.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得( )
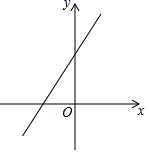
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
9.如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连接CD.若AB=4cm.则△BCD的面积为( )
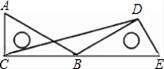
A.4![]() B.2
B.2![]() C.3 D.2
C.3 D.2
10.如图,以正方形ABCD的边AB为一边向外作等边三角形ABE,则∠BED的度数为( )
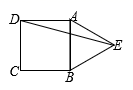
A.55° B.45° C.40° D.42.5°
二、填空题(本大题共有6小题,每小题3分,共18分)
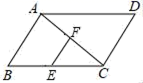
11.如图,在▱ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为_____.
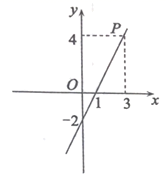
12.若一次函数![]() 的图象如图所示,点
的图象如图所示,点![]() 在函数图象上,则关于x的不等式kx+b≤4的解集是________.
在函数图象上,则关于x的不等式kx+b≤4的解集是________.
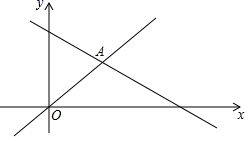
13.如图,函数![]() 和
和![]() 的图象交于点
的图象交于点![]() ,则不等式
,则不等式![]() 的解集是_____.
的解集是_____.
14.菱形的两条对角线长分别是6和8,则菱形的边长为_____.
15.![]() 的小数部分为_________.
的小数部分为_________.
16.在□ABCD中,∠A=105º,则∠D=__________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)先化简在求值: ![]() ,其中
,其中 ![]()
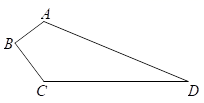
18.(8分)某小区有一块四边形空地ABCD,如图所示,现计划在这块地上种植每平方米60元的草坪用以美化环境,施工人员测得(单位:米):AB=3,BC=4,CD=12,DA=13,∠B=90°,求小区种植这种草坪需多少钱?
19.(8分)已知抛物线![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() ,
,
(1)若![]() ,
,![]() 时,求线段
时,求线段![]() 的长,
的长,
(2)若![]() ,
,![]() 时,求线段
时,求线段![]() 的长,
的长,
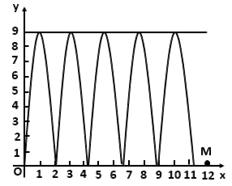
(3)若一排与![]() 形状相同的抛物线在直角坐标系上如图放置,且每相邻两个的交点均在
形状相同的抛物线在直角坐标系上如图放置,且每相邻两个的交点均在![]() 轴上,
轴上,![]() ,若
,若![]() 之间有5个它们的交点,求
之间有5个它们的交点,求![]() 的取值范围.
的取值范围.
20.(8分)已知三角形纸片ABC,其中∠C=90°,AB=10,BC=6,点E,F分别是AC,AB上的点,连接EF.
(1)如图1,若将纸片ABC沿EF折叠,折叠后点A刚好落在AB边上点D处,且S△ADE=S四边形BCED,求ED的长;
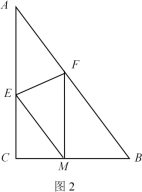
(2)如图2,若将纸片ABC沿EF折叠,折叠后点A刚好落在BC边上点M处,且EM∥AB.
①试判断四边形AEMF的形状,并说明理由;
②求折痕EF的长.

21.(8分)问题发现:
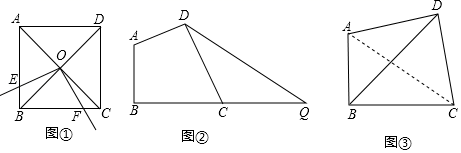
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
22.(10分)如图,在平面直角坐标系中,正方形![]() 两顶点为
两顶点为![]() ,
,![]() ,点D的坐标为
,点D的坐标为![]() ,在
,在![]() 上取点E,使得
上取点E,使得![]() ,连接
,连接![]() ,分别交
,分别交![]() ,
,![]() 于M,N两点.
于M,N两点.
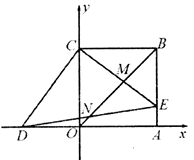
(1)求证:![]() ;
;
(2)求点E的坐标和线段![]() 所在直线的解析式;
所在直线的解析式;
(3)在M,N两点中任选一点求出它的坐标.
23.(10分)四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
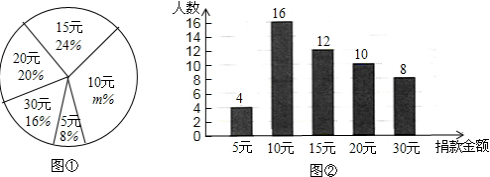
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
24.(12分)解方程:x2﹣6x﹣4=1.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、D
4、A
5、B
6、C
7、B
8、A
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、x≤1
13、![]()
14、1
15、![]() ﹣1.
﹣1.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、-![]()
18、小区种植这种草坪需要2160元.
19、(1)6;(2)6;(3)![]()
20、(1)DE=1;(2)①四边形AEMF是菱形,证明见解析;②![]()
21、(1)4;(2)5![]() ;(3)600(
;(3)600(![]() +1).
+1).
22、(1)详见解析;(2)点E的坐标是![]() ,
,![]() ;(3)点M的坐标为
;(3)点M的坐标为![]() ,或点N的坐标为
,或点N的坐标为![]() .
.
23、(1)50; 1;(2)2;3;15;(3)608人.
24、x1=3+![]() ,x2=3﹣
,x2=3﹣![]() .
.
相关试卷
这是一份林芝2022-2023学年七下数学期末达标检测模拟试题含答案,共5页。试卷主要包含了下列命题是假命题的是,把根号外的因式移入根号内,结果等内容,欢迎下载使用。
这是一份安徽省马鞍市培正学校2022-2023学年七下数学期末达标检测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,已知反比例函数y等内容,欢迎下载使用。
这是一份安徽省宿州市鹏程中学2022-2023学年七下数学期末达标检测模拟试题含答案,共6页。试卷主要包含了已知分式方程,去分母后得等内容,欢迎下载使用。












