


安徽省“六校联盟”2022-2023学年七下数学期末达标检测模拟试题含答案
展开安徽省“六校联盟”2022-2023学年七下数学期末达标检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.下列成语所描述的事件为随机事件的是( )
A.守株待兔 B.水中捞月 C.瓮中捉鳖 D.拔苗助长
2.在同一平面直角坐标系中,函数![]() 与
与![]() 的图象可能是( )
的图象可能是( )
A.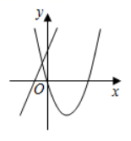 B.
B. 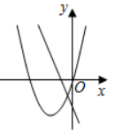
C.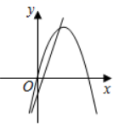 D.
D.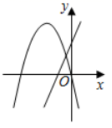
3.如图,![]() 中,
中,![]() ,
,![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
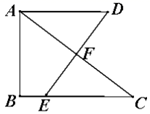
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.药品研究所开发一种抗菌新药,经过多年的动物实验之后首次用于临床人体试验,测得成人服药后血液中药物浓度![]() (微克/毫升)与服药后的时间
(微克/毫升)与服药后的时间![]() (时)之间的函数关系如图所示,则当
(时)之间的函数关系如图所示,则当![]() ,
,![]() 的取值范围是( )
的取值范围是( )
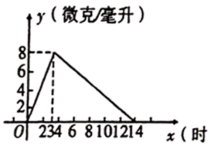
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=![]() (x<0)的图象经过点C,则k的值为( )
(x<0)的图象经过点C,则k的值为( )
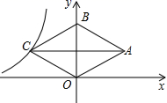
A.24 B.-12 C.-6 D.±6
6.二次函数y1=ax2+bx+c与一次函数y2=mx+n的图象如图所示,则满足ax2+bx+c>mx+n的x的取值范围是( )
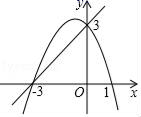
A.﹣3<x<0 B.x<﹣3或x>0 C.x<﹣3 D.0<x<3
7.如图,先将矩形ABCD沿三等分线折叠后得到折痕PQ,再将纸片折叠,使得点A落在折痕PQ上E点处,此时折痕为BF,且AB=1.则AF的长为( )
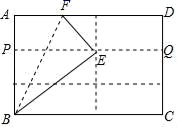
A.4 B.![]() C.
C.![]() D.
D.![]()
8.在一次“爱心互助”捐款活动中,某班第一小组7名同学捐款的金额(单位:元)分别为6,3,6,5,5,6,9.这组数据的中位数和众数分别是( )
A.5,5 B.6,6 C.6,5 D.5,6
9.证明:平行四边形对角线互相平分.
已知:四边形ABCD是平行四边形,如图所示.
求证:![]() ,
,![]()
以下是排乱的证明过程,正确的顺序应是
①![]() ,
,![]() .②
.②![]() 四边形ABCD是平行四边形.③
四边形ABCD是平行四边形.③![]() ,
,![]() .④
.④![]() .⑤
.⑤![]() ,
,![]() ( )
( )
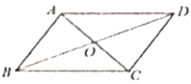
A.②①③④⑤ B.②③⑤①④ C.②③①④⑤ D.③②①④⑤
10.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,一条对角线被另一条对角线平分;③一组对边相等,一条对角线被另一条对角线平分;④两组对角的平分线分别平行,不能判定为平行四边形的是( )
A.① B.② C.③ D.④
二、填空题(本大题共有6小题,每小题3分,共18分)
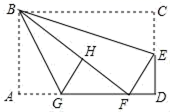
11.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
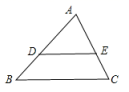
12.如图,DE∥BC,![]() ,则
,则![]() =_______.
=_______.
13.比较大小:![]() ________
________![]() .
.
14.无论x取何值,分式![]() 总有意义,则m的取值范围是______.
总有意义,则m的取值范围是______.
15.已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=﹣3,x2=4,则m+n=_____.
16.已知正比例函数y=kx的图象经过点A(﹣1,2),则正比例函数的解析式为 .
三、解下列各题(本大题共8小题,共72分)
17.(8分)在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E、F分别在边
,点E、F分别在边![]() 、
、![]() 上,
上,![]() ,点P与
,点P与![]() 在直线
在直线![]() 的两侧,
的两侧,![]() ,
,![]() ,射线
,射线![]() 、
、![]() 与边
与边![]() 分别相交于点M、N,设
分别相交于点M、N,设![]() ,
,![]() .
.
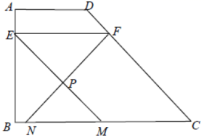
(1)求边![]() 的长;
的长;
(2)如图,当点P在梯形![]() 内部时,求关于x的函数解析式,并写出定义域;
内部时,求关于x的函数解析式,并写出定义域;
(3)如果![]() 的长为2,求梯形
的长为2,求梯形![]() 的面积.
的面积.
18.(8分)为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 ![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 成正比例;燃烧后,
成正比例;燃烧后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 分钟燃完,此时教室内每立方米空气含药量为
分钟燃完,此时教室内每立方米空气含药量为![]() .根据以上信息解答下列问题:
.根据以上信息解答下列问题:
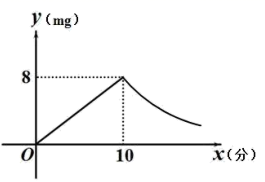
(1)分别求出药物燃烧时及燃烧后 ![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当每立方米空气中的含药量低于![]() 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于![]() 的持续时间超过
的持续时间超过![]() 分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
19.(8分)在平面直角坐标系xOy中,点P和图形W的“中点形”的定义如下:对于图形W上的任意一点Q,连结PQ,取PQ的中点,由所以这些中点所组成的图形,叫做点P和图形W的“中点形”.
已知C(-2,2),D(1,2),E(1,0),F(-2,0).
(1)若点O和线段CD的“中点形”为图形G,则在点![]() ,
,![]() ,
,![]() 中,在图形G上的点是 ;
中,在图形G上的点是 ;
(2)已知点A(2,0),请通过画图说明点A和四边形CDEF的“中点形”是否为四边形?若是,写出四边形各顶点的坐标,若不是,说明理由;
(3)点B为直线y=2x上一点,记点B和四边形CDEF的中点形为图形M,若图形M与四边形CDEF有公共点,直接写出点B的横坐标b的取值范围.
20.(8分)化简求值:已知![]() ,求
,求![]() 的值.
的值.
21.(8分)已知Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a,b,c,设△ABC的面积为S.
(1)填表:
三边a,b,c | S | c+b-a | c-b+a |
3,4,5 |
| 6 |
|
5,12,13 |
| 20 |
|
8,15,17 |
| 24 |
|
(2)①如果m=(c+b-a)(c-b+a),观察上表猜想S与m之间的数量关系,并用等式表示出来.
②证明①中的结论.
22.(10分)如图1,![]() ,
,![]() 是线段
是线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边,在
为边,在![]() 的同侧构造菱形
的同侧构造菱形![]() 和菱形
和菱形![]() ,
,![]() 三点在同一条直线上连结
三点在同一条直线上连结![]() ,设射线
,设射线![]() 与射线
与射线![]() 交于
交于![]() .
.
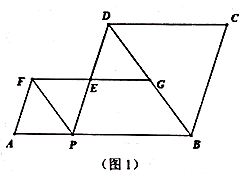
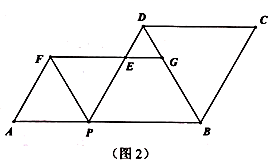
(1)当![]() 在点
在点![]() 的右侧时,求证:四边形
的右侧时,求证:四边形![]() 是平形四边形.
是平形四边形.
(2)连结![]() ,当四边形
,当四边形![]() 恰为矩形时,求
恰为矩形时,求![]() 的长.
的长.
(3)如图2,设![]() ,
,![]() ,记点
,记点![]() 与
与![]() 之间的距离为
之间的距离为![]() ,直接写出
,直接写出![]() 的所有值.
的所有值.
23.(10分)如图,在平面直角坐标系中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象都经过点
的图象都经过点![]() .
.
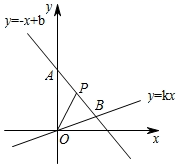
(1)求一次函数和正比例函数的解析式;
(2)若点![]() 是线段
是线段![]() 上一点,且在第一象限内,连接
上一点,且在第一象限内,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于
关于![]() 的函数解析式.
的函数解析式.
24.(12分)某公司销售人员15人,销售经理为了制定某种商品的月销售定额,统计了这15人某月的销售量如表所示:
每人销售量/件 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)这15位营销人员该月销售量的中位数是______,众数是______;
(2)假设销售部负责人把每位销售人员的月销售额定为210件,你认为是否合理?如不合理,请你制定一个较为合理的销售定额,并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、D
4、C
5、C
6、A
7、C
8、B
9、C
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、①②④.
12、![]()
13、<
14、m>1
15、-1
16、y=﹣1x
三、解下列各题(本大题共8小题,共72分)
17、(1)6;(2)y=-3x+10(1≤x<![]() );(2)
);(2)![]() 或32
或32
18、(1)![]() ,
,![]() ;(2)第
;(2)第![]() 分至
分至![]() 分内消毒人员不可以留在教室里;(3)本次消毒有效.
分内消毒人员不可以留在教室里;(3)本次消毒有效.
19、(1)![]() ,
,![]() ;(1)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(
;(1)点A和四边形CDEF的“中点形”是四边形,各顶点的坐标为:(0,0)、(0,1)、(![]() ,0)、(
,0)、(![]() ,1);(3)-1≤b≤0或 1≤b≤1.
,1);(3)-1≤b≤0或 1≤b≤1.
20、![]() ;14
;14
21、(1)6,30,60,4,6,10;(2)①S=![]() m;②见解析
m;②见解析
22、(1)见解析;(2)FG=![]() ;(3)d=14或
;(3)d=14或![]() .
.
23、(1)y=﹣x+4,![]() ;(2)S=2x(0<x≤3).
;(2)S=2x(0<x≤3).
24、(1)210,210;(2)合理,理由见解析
河北省唐山丰南区六校联考2022-2023学年数学七下期末达标检测模拟试题含答案: 这是一份河北省唐山丰南区六校联考2022-2023学年数学七下期末达标检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,六边形的内角和是,函数的自变量的取值范围是,函数y=中,自变量的取值范围是,若,则下列各式中,错误的是等内容,欢迎下载使用。
广东省湛江地区六校联考2022-2023学年数学七下期末达标检测模拟试题含答案: 这是一份广东省湛江地区六校联考2022-2023学年数学七下期末达标检测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,某校有15名同学参加区数学竞赛等内容,欢迎下载使用。
安徽省庐阳区五校联考2022-2023学年数学七下期末达标检测模拟试题含答案: 这是一份安徽省庐阳区五校联考2022-2023学年数学七下期末达标检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列调查中,适合采用普查的是,下列式子因式分解正确的是,下列说法正确的是等内容,欢迎下载使用。












