


云南省怒江市2022-2023学年七下数学期末综合测试试题含答案
展开云南省怒江市2022-2023学年七下数学期末综合测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.若一个多边形的每一个外角都是40°,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
2.如图,在矩形ABCD中,E为AD的中点,∠BED的平分线交BC于点F,若AB=3,BC=8,则FC的长度为( )
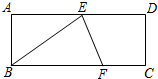
A.6 B.5 C.4 D.3
3.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,则
,则![]() ()
()
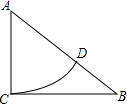
A.2.5 B.3 C.2 D.3.5
4.在一次统考中,从甲、乙两所中学初二学生中各抽取50名学生进行成绩分析,甲校的平均分和方差分别是82分和245分,乙校的平均分和方差分别是82分和190分,根据抽样可以粗略估计成绩较为整齐的学校是( )
A.甲校 B.乙校 C.两校一样整齐 D.不好确定哪校更整齐
5.已知不等式mx+n>2的解集是x<0,则下列图中有可能是函数y=mx+n的图象的是( )
A.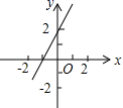 B.
B.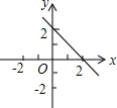 C.
C.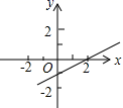 D.
D.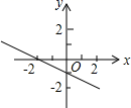
6.如表记录了甲、乙、丙、丁四名学生最近几次数学综合测试成绩的平均数与方差:
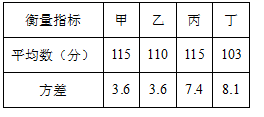
根据表中数据,要从中选择一名成好且发挥稳定的同学参加竟赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
7.如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则对四边形EFGH表述最确切的是( )
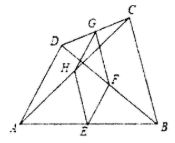
A.四边形EFGH是矩形 B.四边形EFGH是菱形
C.四边形EFGH是正方形 D.四边形EFGH是平行四边形
8.如图,在△ABC中,∠B=45°,∠ACB=60°,AB=16,AD⊥BC,垂足为D,∠ACB的平分线交AD于点E,则AE的长为( )
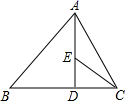
A.![]() B.4
B.4![]() C.
C.![]()
![]() D.6
D.6![]()
9.如图,若正比例函数y=kx图象与四条直线x=1,x=2,y=1,y=2相交围成的正方形有公共点,则k的取值范围是( )
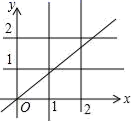
A.k≤2 B.k≥![]() C.0<k<
C.0<k<![]() D.
D.![]() ≤k≤2
≤k≤2
10.使式子![]() 有意义的x的值是( )
有意义的x的值是( )
A.x≥1 B.x≤1 C.x≥﹣1 D.x≤2
二、填空题(本大题共有6小题,每小题3分,共18分)
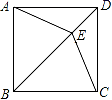
11.如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE=_____.
12.若x1,x2是一元二次方程x2+x﹣2=0的两个实数根,则x1+x2+x1x2=_____.
13.如图,一次函数y=-2x+2的图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,以线段
,以线段![]() 为直角边在第一象限内作等腰直角三角形ABC,且
为直角边在第一象限内作等腰直角三角形ABC,且![]() ,则点C坐标为_____.
,则点C坐标为_____.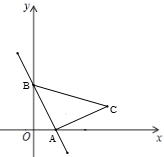
14.甲,乙,丙三位同学近![]() 次快速阅读模拟比赛成绩平均分均为
次快速阅读模拟比赛成绩平均分均为![]() 分,且甲,乙,丙的方差是
分,且甲,乙,丙的方差是![]() ,则发挥最稳定的同学是__________.
,则发挥最稳定的同学是__________.
15.如图,△ABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作EF∥AC,得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1,E1,连接D1E1,作E1F1∥EF,得到四边形E1D1FF1,它的周长记作C2…照此规律作下去,则C2018=_____.
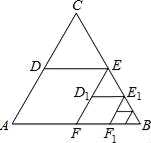
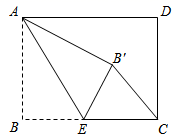
16.如图,矩形纸片![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,沿
边上,沿![]() 折叠纸片,使点
折叠纸片,使点![]() 落在点
落在点![]() 处,连结
处,连结![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为______.
的长为______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销量y(件)之间的关系如下表:若日销量y是销售价x的一次函数.
(1)求出日销量y(件)与销售价x(元)的函数关系式;
(2)求销售定价为30元时,每日的销售利润.
x(元) | 15 | 20 | 25 | …… |
y(件) | 25 | 20 | 15 | …… |
18.(8分)在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
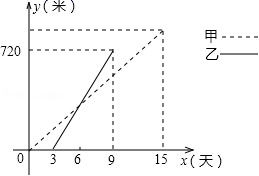
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
19.(8分)如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F. 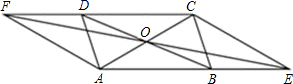
求证:四边形AECF是平行四边形.
20.(8分)在平面直角坐标系中,如果点![]() 、点
、点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 、
、![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 、
、![]() 的“极好菱形”,如图为点
的“极好菱形”,如图为点![]() 、
、![]() 的“极好菱形”的一个示意图.
的“极好菱形”的一个示意图.
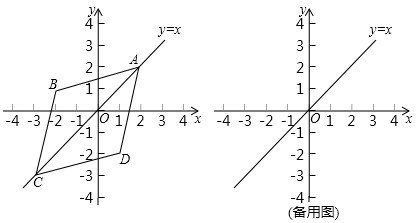
(1)点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“极好菱形”的顶点的是_______.
的“极好菱形”的顶点的是_______.
(2)若点![]() 、
、![]() 的“极好菱形”为正方形,则这个正方形另外两个顶点的坐标是________.
的“极好菱形”为正方形,则这个正方形另外两个顶点的坐标是________.
(3)如果四边形![]() 是点
是点![]() 、
、![]() 的“极好菱形”
的“极好菱形”
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积
的面积
②当四边形![]() 的面积为
的面积为![]() ,且与直线
,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
21.(8分)甲、乙两台机床同时生产一种零件.在连续![]() 周中,两台机床每周出次品的数量如下表.
周中,两台机床每周出次品的数量如下表.
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)分别计算两组数据的平均数与方差;
(2)两台机床出次品的平均数怎样?哪台机床出次品的波动性小?
22.(10分)我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形.
,所以这个三角形是常态三角形.
(1)若![]() 三边长分别是2,
三边长分别是2,![]() 和4,则此三角形 常态三角形(填“是”或“不是”
和4,则此三角形 常态三角形(填“是”或“不是” ![]() ;
;
(2)如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() 是常态三角形,求
是常态三角形,求![]() 的面积.
的面积.
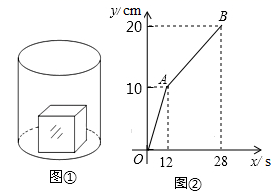
23.(10分)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
24.(12分)为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
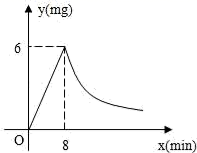
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
参考答案
一、选择题(每小题3分,共30分)
1、C
2、D
3、C
4、B
5、B
6、A
7、B
8、C
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、22.5°
12、-3
13、 (3,1);
14、丙
15、![]()
16、3或![]()
三、解下列各题(本大题共8小题,共72分)
17、 (1) y=﹣x+1;(2)200元
18、(1)120米(2)y乙=120x﹣1,y甲=60x(3)2
19、详见解析
20、 (1) ![]() ,
,![]() ;
;
(1) (1,3)、(3,1);
(3)①1;②-2≤b≤2.
21、(1)甲的平均数为:![]() ;乙的平均数为:
;乙的平均数为:![]() ;甲的方差为:
;甲的方差为:![]() ;乙的方差为:
;乙的方差为:![]() ;
;
(2)两台机床出次品的平均数相同;甲机床出次品的波动性小.
22、(1)是;(2)![]() 或
或![]() .
.
23、(1)10;(2)y=![]() x+
x+![]() (12≤x≤28);(3)4 s.
(12≤x≤28);(3)4 s.
24、(1)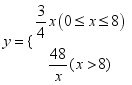 ;(2)至少需要30分钟后生才能进入教室.(3)这次消毒是有效的.
;(2)至少需要30分钟后生才能进入教室.(3)这次消毒是有效的.
精品解析:云南省怒江州泸水市怒江新城新时代中学2022-2023学年八年级下学期期末考试数学试题: 这是一份精品解析:云南省怒江州泸水市怒江新城新时代中学2022-2023学年八年级下学期期末考试数学试题,文件包含精品解析云南省怒江州泸水市怒江新城新时代中学2022-2023学年八年级下学期期末考试数学试题原卷版docx、精品解析云南省怒江州泸水市怒江新城新时代中学2022-2023学年八年级下学期期末考试数学试题解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
云南省怒江市2023-2024学年八上数学期末质量跟踪监视试题含答案: 这是一份云南省怒江市2023-2024学年八上数学期末质量跟踪监视试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列运算正确的是,下列命题是假命题的是,计算等内容,欢迎下载使用。
怒江市重点中学2022-2023学年数学七下期末监测试题含答案: 这是一份怒江市重点中学2022-2023学年数学七下期末监测试题含答案,共6页。试卷主要包含了下列计算正确的是等内容,欢迎下载使用。












