黑龙江省庆安县2022-2023学年七下数学期末统考试题含答案

黑龙江省庆安县2022-2023学年七下数学期末统考试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．在一个直角三角形中，已知两直角边分别为6cm，8cm，则下列结论不正确的是（　　）

A．斜边长为10cm B．周长为25cm

C．面积为24cm2 D．斜边上的中线长为5cm

2．若，则的值用、可以表示为                     （　 　）

A． B． C． D．

3．如图，已知点A（1，0），点B（b，0）（b＞1），点P是第一象限内的动点，且点P的纵坐标为，若△POA和△PAB相似，则符合条件的P点个数是（　　）

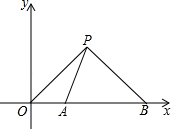
A．0 B．1 C．2 D．3

4．若a,b,c满足则关于x的方程的解是(  )

A．1，0 B．-1，0 C．1，-1 D．无实数根

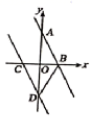
5．如图，已知一条直线经过点、点，将这条直线向左平移与轴、轴分别交于点、点．若，则直线的函数解析式为（　　）

A． B． C． D．

6．用反证法证明：“直角三角形至少有一个锐角不小于45°”时，应先假设（   ）

A．直角三角形的每个锐角都小于45°

B．直角三角形有一个锐角大于45°

C．直角三角形的每个锐角都大于45°

D．直角三角形有一个锐角小于45°

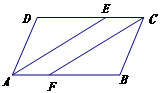
7．如图,平行四边形ABCD中,∠BDC=30°，DC=4,AE⊥BD于E，CF⊥BD于F，且E、F恰好是BD的三等分点，AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是(     )

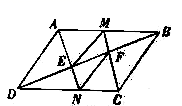
A． B． C．2 D．2

8．如图，在中，，，，为边上一动点，于点，于点，则的最小值为(    )

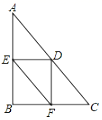
A．2.4 B．3 C．4.8 D．5

9．已知x（x﹣2）＝3，则代数式2x2﹣4x﹣7的值为（　　）

A．6 B．﹣4 C．13 D．﹣1

10．我市某一周每天的最高气温统计如下（单位：℃）：27，28，1，28，1，30，1．这组数据的众数与中位数分别是（    ）．

A．28，28 B．28，1 C．1，28 D．1，1

11．某班数学兴趣小组位同学的一次数学测验成绩为，，，，(单位：分)，经过计算这组数据的方差为，小李和小明同学成绩均为分，若该组加入这两位同学的成绩则(    )

A．平均数变小 B．方差变大 C．方差变小 D．方差不变

12．某中学规定学生的学期体育成绩满分为100分，其中课外体育占20%，期中考试成绩占30%，期末考试成绩占50%.小彤的这三项成绩（百分制）分别为95分，90分，88分，则小彤这学期的体育成绩为（）

A．89分 B．90分 C．92分 D．93分

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，正方形ABCD的边长为2，MN∥BC分别交AB、CD于点M、N，在MN上任取两点P、Q，那么图中阴影部分的面积是_____．

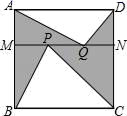
14．在平行四边形ABCD中，∠A+∠C＝200°，则∠A＝_____．

15．用反证法证明命题“三角形中至少有两个锐角”，第一步应假设_____．

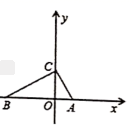
16．如图，在中，，，斜边在轴上，点在轴正半轴上，点的坐标为.则直角边所在直线的解析式为__________．

17．两个全等的直角三角尺如图所示放置在∠AOB的两边上，其中直角三角尺的短直角边分别与∠AOB的两边上，两个直角三角尺的长直角边交于点P，连接OP，且OM＝ON，若∠AOB＝60°，OM＝6，则线段OP＝______．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）为迎接省“义务教育均衡发展验收”，某广告公司承担了制作宣传牌任务，安排甲、乙两名工人制作，由于乙工人采用了新式工具，其工作效率比甲工人提高了20％，同样制作30个宣传牌，乙工人比甲工人节省了一天时间:

(1)求甲乙两名工人每天各制作多少个宣传牌?

(2)现在需要这两名工人合作完成44个宣传牌制作在务，应如何分配，才能让两名工人同时完成任务?

19．（5分）如图，在边长为1个单位的长度的正方形网格中有一个格点（顶点都在格点上）.

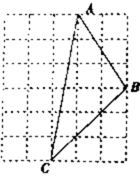
（1）请用无刻度直尺画出另一个格点，使与的面积相等；

（2）求出的面积.

20．（8分）如图，在平面直角坐标系中，为坐标原点，矩形的顶点、，将矩形的一个角沿直线折叠，使得点落在对角线上的点处，折痕与轴交于点.

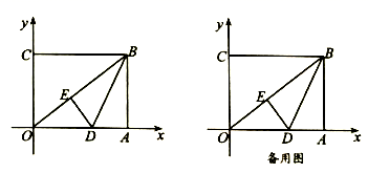
（1）线段的长度为__________；

（2）求直线所对应的函数解析式；

（3）若点在线段上，在线段上是否存在点，使四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由.

21．（10分）如图，在中，分别是的平分线．

求证：四边形是平行四边形．

22．（10分）射阳县实验初中为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：

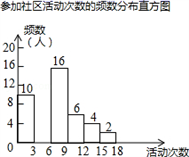
参加社区活动次数的频数、频率分布表

根据以上图表信息，解答下列问题：

（1）表中a=　　，b=　　；

（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；

（3）若该校共有1200名学生，请估计该校在上学期参加社区活动超过6次的学生有多少人？

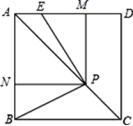
23．（12分）如图，已知正方形ABCD的边长为1，P是对角线AC上任意一点，E为AD上的点，且∠EPB=90°，PM⊥AD，PN⊥AB．

（1）求证：四边形PMAN是正方形；

（2）求证：EM=BN；

（3）若点P在线段AC上移动，其他不变，设PC=x，AE=y，求y关于x的解析式．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、C

3、D

4、C

5、A

6、A

7、B

8、C

9、D

10、D

11、C

12、B

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、1

14、100°

15、同一三角形中最多有一个锐角　．

16、y=x+1

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、 (1)甲工人每天制作5个宣传牌，乙工人每天制作6个；(2)给甲分配制作20个，乙制作24个.

19、 (1)详见解析;(2)

20、（1）1；（2）；（3）

21、详见解析.

22、（1）12；0.08 （2）12（3）672

23、 (1)见解析;(2)见解析;(3) y=﹣x+1.