教科版2019 高中物理必修第二册 第四章 课件+教案

动能 动能定理

【教学目标】

1．明确动能的表达式及含义。

2．能理解和推导动能定理。

3．掌握动能定理及其应用。

【教学重点】

能理解和推导动能定理。

【教学难点】

掌握动能定理及其应用。

【教学过程】

一、情境导入

我们在初中物理课程中学过，功和能是两个联系密切的物理量，一个物体能够对其他物体做功，我们就说这个物体具有能量（energy），如高速运动的子弹能击穿苹果，海啸（高速运动的海水）能掀翻汽车、摧毁房屋，风（高速运动的空气）能推动叶片转动，这些都说明运动的物体可以做功，具有能量。那什么是动能，什么是动能定理？

二、新知学习

（一）动能

1．定义：物体由于运动而具有的能量。

2．表达式：Ek＝mv2。

3．单位：与功的单位相同，国际单位为焦耳。

1 J＝1 N·m＝1 kg·m2/s2。

4．标量：没有方向。Ek≥0，即动能总为非负值。

（二）动能定理

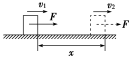
1．理论推导：如图所示，质量为m的物体在沿运动方向的合外力作用下发生位移x，速度由v1增大到v2，则W＝ΔEk。

2．动能定理

（1）内容：合外力所做的功等于物体动能的变化。

（2）表达式：①W＝ΔEk＝Ek2－Ek1。

②W＝mv－mv。

说明：A．式中W为合力所做的功，它等于各力做功的代数和。

B．如果外力做正功，物体的动能增加，外力做负功，物体的动能减少。

（3）适用范围：不仅适用恒力做功和直线运动，也适用于变力做功和曲线运动情况。

（三）动能定理的实验证明

（1）实验装置：应用“探究a与F、m之间的定量关系”的实验装置，如图所示。

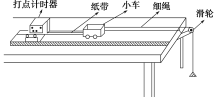
（2）实验原理：从打出的纸带及拉力F与小车质量的数据进行分析，利用纸带测量数据，计算小车打下各计数点时的瞬时速度，进而验证小车运动到打下各计数点过程中合外力对它做的功W与动能增加量ΔEk的相等关系。

（3）实验结论：W＝ΔEk。

【想一想】

一个物体如果在运动过程中，其动能保持不变，则这个物体一定做匀速直线运动吗？

提示：由Ek＝mv2可知，物体的动能保持不变，只能说mv2的大小不变，其中物体运动的速度方向有可能是变化的，如物体做匀速圆周运动时，其运动的动能也是不变的。

三、重难点突破

（一）对动能定理的理解

1．相似关系对比

2．应用动能定理解题的步骤

（1）确定研究对象和研究过程。

（2）对研究对象进行受力分析。

（3）写出该过程中合外力做的功，或分别写出各个力做的功（注意功的正负）。如果研究过程中物体受力情况有变化，要分别写出该力在各个阶段做的功。

（4）写出物体的初、末动能。

（5）按照动能定理列式求解。

3．应用动能定理的优越性

功的计算公式W＝Fxcos α只能求恒力做的功，不能求变力的功，而由于动能定理提供了一个物体的动能变化ΔEk与合外力对物体所做功具有等量代换关系，因此已知（或求出）物体的动能变化ΔEk＝Ek2－Ek1，就可以间接求得变力做功。

【特别提醒】W为合力的功或各个外力做功的代数和，有正、负之分，注意ΔEk＝Ek末－Ek初，顺序不可颠倒。

【例1】一个物体放在光滑的水平地面上，现用水平力F拉着物体由静止开始运动，当经过位移x1时，速度达到v，随后又经过位移x2时，速度达到2v。那么，在x1和x2两段路程中F对物体做的功之比为（   ）

A．1:2   B．2:1

C．1:3  D．1:4

【解析】物体在前进x1的过程中，对物体受力分析可得，只有拉力F对物体做功

由动能定理得W1＝Fx1＝mv2

物体在前进x2的过程中，对物体受力分析可得，只有拉力F对物体做功

由动能定理得W2＝Fx2＝m（2v）2－mv2

联立上面两式可得，在两个过程中力F做的功之比为＝。

【借题发挥】本题中的合外力为恒力，还可用牛顿运动定律求解，但在变力作用的情况下，牛顿运动定律就不能使用了，而动能定理仍可使用。

（二）动能定理在多个过程或多个物体问题中的应用

1．动能定理在多个过程问题中的应用

（1）对于多个物理过程要仔细分析，将复杂的过程分割成一个一个子过程，分别对每个过程分析，得出每个过程遵循的规律，当每个过程都可以运用动能定理时，可以选择分段或全程应用动能定理更简单、方便。

（2）应用全程法解题求功时，有些力不是全过程都作用的，必须根据不同的情况分别对待，弄清楚物体所受的力在哪段位移上做功，哪些力做功，做正功还是负功，正确写出总功。

2．动能定理在两个（或多个）相互关联的物体系统中的应用

（1）从严格意义上讲课本上讲的动能定理是质点的动能定理，即质点动能的增量等于作用于质点的合外力所做的功。对于由相互作用的若干质点组成的系统，动能的增量在数值上等于一切外力所做的功与一切内力所做功的代数和，称为系统动能定理。

（2）由于作用力与反作用力的功的代数和不一定等于零，所以对于系统只考虑外力做功而应用动能定理很可能要犯错，所以往往把系统内各质点隔离分析，分别应用动能定理比较合适。

【特别提醒】

（1）应用动能定理最大的优势在于不要求深入研究过程变化的细节，对不涉及物体运动过程中的加速度和时间问题的，无论恒力做功还是变力做功，一般用动能定理求解。

（2）应用动能定理求力对物体做功时，位移应是物体相对地面的位移，而动能Ek＝mv2中“v”应是物体对地的速度。

【方法总结】对这种多过程问题，可以分段利用动能定理求解，也可以对全过程利用动能定理求解，解题时可根据具体情况选择使用。

（三）动能定理与牛顿运动定律的比较

两种思路对比可以看出应用动能定理解题不涉及加速度、时间，不涉及矢量运算，运算简单不易出错。

【名师点拨】动能定理、牛顿运动定律与运动学公式相结合是解决力学问题的两种重要方法，有的问题既能用牛顿运动定律与运动学公式相结合的方法解决也能用动能定理解决。

（1）通常情况下，某问题若涉及时间或过程的细节，要用牛顿运动定律与运动学公式相结合的方法去解决；

（2）某问题若不考虑具体细节、状态或时间，一般要用动能定理去解决。