小学整理和复习示范课ppt课件

这是一份小学整理和复习示范课ppt课件，共32页。PPT课件主要包含了“外方内圆”，“外圆内方”，阅读与理解，分析与解答，从图2可以看出，回顾与反思，生活中的数学，÷26厘米，方法一，方法二等内容，欢迎下载使用。

这些图形有什么共同点？
整体是由圆和正方形组成的组合图形。
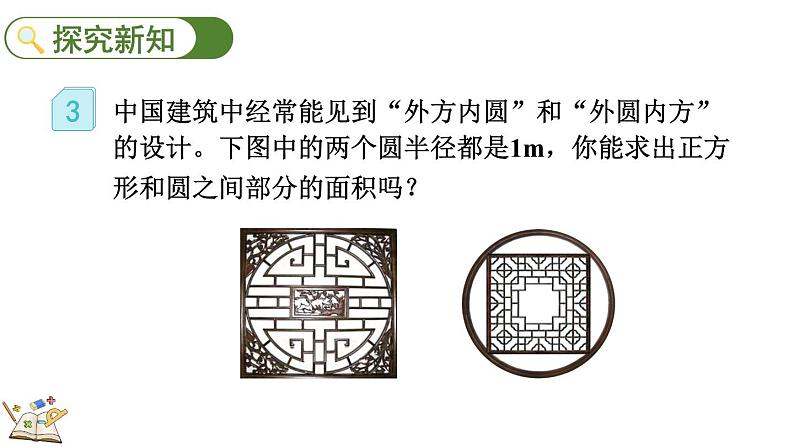
中国建筑中经常能见到“外方内圆”和“外圆内方”的设计。下图中的两个圆半径都是1m，你能求出正方形和圆之间部分的面积吗？
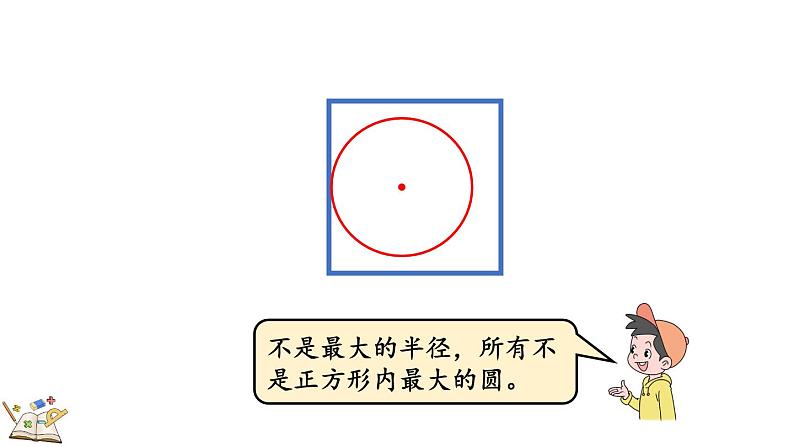
不是最大的半径，所有不是正方形内最大的圆。
我连接正方形的对角线，找到圆心。
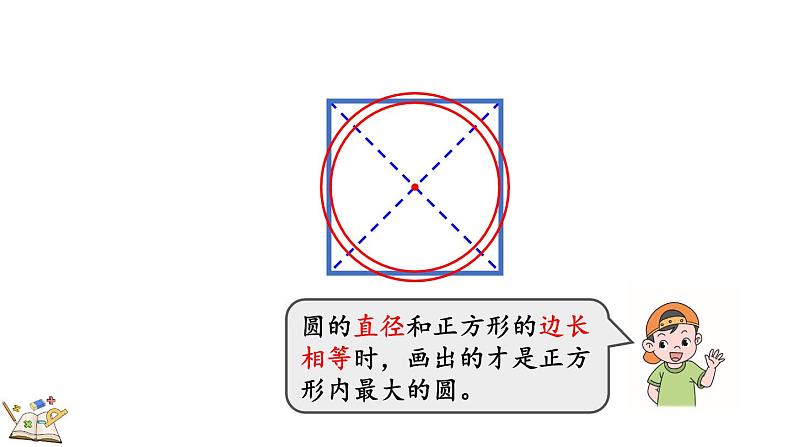
圆的直径和正方形的边长相等时，画出的才是正方形内最大的圆。
以正方形对角线的交点为圆心、以正方形边长的一半为半径。
如果让正方形的四个顶点都在圆上，使它成为圆内最大的正方形，这个圆又该怎样画呢？
正方形对角线的交点是圆心。正方形对角线的一半是半径。
想一想正方形和圆之间的面积有什么联系？
从题目中我们知道了什么？
如何求正方形和圆之间部分的面积？
下图中的两个圆半径都是1m，你能求出正方形和圆之间部分的面积吗？
用较大的面积减去较小的面积。
要求出圆的面积、正方形的面积。
从图（1）可以看出：（1+1）×（1+1）＝4（m²）
4－3.14＝0.86（m²）
3.14×1²＝3.14（m²）
正方形的面积比圆的面积多0.86 m²。
“外方内圆”中正方形的边长与圆的直径长度相等。
可是“外圆内方”中正方形的边长是多少呢？
可以把“外圆内方”中的正方形看成两个三角形，它的底和高分别是圆的直径和半径。
3.14－2＝1.14（m²）
圆的面积比正方形的面积多1.14 m²。
图（1）：（2r）²－3.14×r²＝0.86r²
如果两个圆的半径都是r，结果又是怎样的？
答：左图中正方形与圆之间部分的面积是0.86 m²， 右图中圆与正方形之间部分的面积是1.14 m²。
当r＝1m时，和前面的结果完全一致。
右图是一面我国唐代铜镜的背面。铜镜的直径是24cm。外面的圆与内部的正方形之间部分的面积是多少？
答：外面的圆与内部的正方形之间部分的面积约是164.16 cm2。
车轮平面轮廓采用圆形，是利用同一圆的半径都相等的性质，把车轴装在车轮的圆心上。当车轮在地面上滚动的时候，车轴离地面的距离总是等于车轮的半径，因此只要道路平坦，车子就会平稳地在地面上行驶。试想一下，如果车轮是正方形的，为了保持车辆的平稳行驶，道路应该是什么样子的呢？
井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里，并且能恰好盖住井口，这里利用了同一圆的直径都相等的性质。
王师傅做一个零件，零件的形状是圆内接正方形，已知圆的直径为12cm,你能计算出正方形的面积吗？
答：这个正方形的面积是72cm2 。
已知涂色部分三角形的面积是4平方厘米，求圆的面积。
=25.12（平方厘米）
S圆=πr2S△=r2÷2=4平方厘米
答：圆的面积是25.12平方厘米。
已知图中阴影部分的面积是10cm2，求图中环形的面积。
S环=π×(R2−r2)
答：图中环形的面积是31.4平方厘米。
2.可以借助三角形的面积，计算正方形的面积， 再算面积差。
1.“外方内圆”和“外圆内方”都可以用较大 的面积减去较小的面积。
1.教材第70页练习十五第9题；2.从课时练中选取。