


【同步教案】北师大版数学八年级上册--5.3 应用二元一次方程组—鸡兔同笼 教案
展开应用二元一次方程组 ——鸡兔同笼
【教学目标】
一、教学知识点
1.会用二元一次方程组解决实际问题。
2.在解决实际问题的过程中,用方程组这样的数学模型刻画现实世界。
二、能力训练要求
1.在列方程组的建模过程中,强化方程的模型思想,培养学生列方程解决现实问题的意识和应用能力。
2.将解方程组的技能训练与实际问题的解决融为一体,进一步提高解方程组的技能。
三、情感与价值观要求
1.体会方程组是刻画现实世界的有效数学模型,培养应用数学的意识。
2.在用方程组解决实际问题的过程中,体验数学的实用性,提高学习数学的兴趣。
【教学重点】
1.让学生经历和体验到方程组解决实际问题的过程。
2.进一步体会方程(组)是刻画现实世界的有效数学模型,培养学生的数学应用能力。
【教学难点】
用方程(组)这样的数学模型刻画和解决实际问题,即数学建模的过程。
【教学方法】
自主发现法。
学生在教师的启发引导下通过对具体实际的问题分解,组织学生自主交流,探索去发现列方程建模的过程,从而激发学生学习数学的兴趣,培养学生应用数学的意识。
【课时安排】
4课时
【教学准备】
投影片一张:鸡兔同笼。
【教学过程】
一、提出问题,激发兴趣
[师]我们本章的开头就介绍过“鸡兔同笼”的问题,这节课我们接着用方程来解决此问题,看结果如何?
二、讲授新课
出示投影片
1.今有鸡兔同笼,上有三十五头,下有九十四足,问鸡、兔各有几只? (1)“上有三十五头”“下有九十四足”如何解释? (2)你能根据(1)中的数量关系列出方程组吗? (3)你能解决这样的问题吗? 2.有2元,5元,10元人民币共50张,合计305元,其中2元的张数与5元的张数相同,三种类型的人民币各有多少张? (1)这个问题和上面的“鸡兔同笼”问题有联系吗? (2)你准备设几个未知数? (3)你能根据题目中的已知量、未知量及它们之间的关系列出方程组吗? (4)你能解决这样的问题吗? |
[师]就上面的问题,我们先分组讨论。
(学生在讨论时,教师可参与到学生的讨论,听学生的想法,以便能及时了解学生的思路)
[师生共析]
1.(1)“上有三十五头”是指“鸡和兔共有35只。即“鸡的只数+兔的只数=35只”。“下有九十四足”是指鸡的腿与兔子的腿的和为94条。即“鸡的腿+兔子的腿=94”。
(2)根据(1)中的数量关系,我们可以假设鸡有x只,兔有y只,可得x+y=35 ①,2x+4y=94 ②,把①和②联立方程组,得
![]()
![]()
(3)解法一:由①得y=35-x ③
把③代入②中,得2x+4(35-x)=94
解得x=23
把x=23代入①,得y=12.
所以原方程组的解为![]()
解法二:②-①×2,得
2y=24
y=12
把y=12代入①,得x=23
所以原方程组的解为![]()
答:鸡有23只,兔子有12只。
和用算术方法和一元一次方程的方法来解“鸡免同笼”的问题来比较,用列二元一次方程组来解决此题会更直观,更容易理解。
2.(1)这个问题类似于“鸡兔同笼”的问题。因为它也是将“2元,5元,10元”的人民币混合在了一起,只知道总共有多少张,合起来共多少元,求2元,5元,10元的人民币各有多少张?
(2)在这个题目中,设两个未知数也可以;设三个未知数也可以。我们先来看设两个未知数的情况。由于2元和5元的张数相同,我们可以各设有x张,10元的张数有y张。
(3)根据题目中的已知条件可找到两个等量关系即:2元的张数+5元的张数+10元的张数=50张,2元的总面值+5元的总面值+10元的总面值=305元,于是我们根据(1)中的未知数列出二元一次方程组:
![]()
![]()
(4)用代入消元法和加减消元法都可解决.可由同学们扮演完成.
解法一:由①得y=50-2x ③
把③代入②,得x=15
把x=15代入③,得y=20
所以原方程组的解为![]()
解法二:①×10-②,得
x=15
把x=15代入①,得y=20
所以原方程组的解为![]()
答:2元和5元的人民币各有15张,10元的人民币有20张.
[议一议]如果2.(2)中设有三个未知数,即如果设2元的人民币有x张,5元的人民币y张,10元的人民币z张,如何列出方程组,求解上述问题呢?
[生]我们在设未知数时,没有利用2元的人民币和5元的人民币张数相等这个条件,因此列出的方程就多出一个,再加上我们刚才的两个相等关系,列出的是一个三元一次方程组即由x=y ①,x+y+z=50 ②,2x+5y+10z=305 ③,组成的三元一次方程组。
[师]我们没有详细地讲过三元一次方程组的解法,但我们借鉴二元一次方程组的基本思路——消元,可以解答这个三元一次方程组.下面我们一同来解方程组
![]()

我们可以将①代入②和③,得二元一次方程组
![]()
解这个二元一次方程组,得
![]()
把y=15代入①得x=15
所以方程组的解为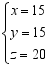
[生]老师,看来解方程组未知数出了并不可怕,关键是掌握解方程组的基本思路——消元。
[师]的确如此。我们学会了解方程组可以解决许多问题。下面我们再来看一下例子。估计大家小学的时候见过。
[例1]以绳测井。若将绳子三折测之,绳子多五尺;若将绳子四折测之,绳子多一尺。绳长、井深各几何?
谁来给大家解释一下题意。
[生]老师,我试一下。这个题目的大意是:用绳子测量水井的深度,如果将绳子三折即折成三等份,则一份绳子的长度要比井多五尺;如果将绳子四折即折成四等份,则一份绳子的长度比井深多一尺。绳长、井深各是多少尺?
[师]这位同学解释得很棒。接下来我们就将此问题转化成数学模型方程组来解决它。首先我们可以从题目中找到相等关系。你知道相等关系蕴含在哪两句话里?你能用含有文字的等式表示出来吗?
[生]可以。我认为相等关系蕴含在“将绳三折测之,绳多五尺”和“若将绳四折测之,绳多一尺”。这两句话中,用等式表示出来为:
绳长÷3-井深=5 ①
绳长÷4-井深=1 ②
[生]老师,我认为相等关系也在这两句话中,但我用下面的等式表示:
绳长-3×井深=5×3 ③
绳长-4×井深=1×4 ④
[师]很好.我们现在设出未知数,设绳长为x尺,井深为y尺,根据①、②得方程组为:

根据③、④得方程组:
![]()
我们观察这两个方程组虽然形式上不同,但我们将第一个方程组中的方程化简,整理便可得出第二个方程组。因此这两个方程组是“同工异曲”的效果。下面我们在练习本上解出方程组的解,你可以任意选其中之一。
(然后让两位学生黑板上板演,教师讲评)
解法一:设绳长x尺,井深y尺,则
![]()

①-②,得![]() =4,
=4,
![]() =4
=4
x=48
将x=48代入①,得y=11
答:绳长48尺,井深11尺.
解法二:设绳子长x尺,井深y尺,则
![]()
![]()
由③-④,得y=11
把y=11代入④,得x=48
答:绳长48尺,井深11尺。
[师生共析]我们在列方程组解决实际问题时,应先分析题目中的已知量、未知量是什么,各个量之间的关系是什么,找出它们之间的相等关系,列出方程(组),建模过程就可完成,因此我们说解决实际问题的建模过程非常重要。
三、随堂练习
![]() 1.解:设每头牛价值“金”x两,每只羊价值“金”y两,则
1.解:设每头牛价值“金”x两,每只羊价值“金”y两,则![]()
由①×2-②×5,得y=![]()
把y=![]() 代入②,得x=
代入②,得x=![]()
所以,每头牛价值“金”![]() 两,每头羊值“金”
两,每头羊值“金”![]() 两。
两。
2.解:设甲带钱x,乙带钱y,
![]() 则
则
由①×2-②,得x=37![]()
把x=37![]() 代入①,得y=25
代入①,得y=25
所以甲带钱37![]() ,乙带钱25。
,乙带钱25。
四、课时小结
本节课我们经历和体验了列方程组解决实际问题的过程,体会到方程组是刻画现实世界的有效模型,从而更进一步提高了我们应用数学的意识及解方程组的技能。
【作业布置】
1.课后习题
2.收集资料:数学史料,以一组为单位办1份数学史料手抄报。
活动与探究:
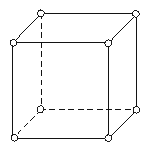
如图,在一个正方体的顶点处填上1~9的数码中的8个,每一个顶点只填一个数码。使得正方体每个面上的四个顶点所填数码之和均为18,那么未被填上的数码是什么?
过程:如果用1~9中的每一个数去试,过程繁琐。根据题意,我们可以利用方程这个数学模型,使问题简单化。
结果:设未被填上的数为x,根据题意,可得:
(1+2+…+9-x)÷2=18
得45-x=36
x=9
所以未被填上的数是9。
【板书设计】
鸡兔同笼 一、鸡兔同笼 解:设鸡、兔各有x只、y只, 根据题意,得:
(由学生演示解方程组的过程) 二、例题讲解 课后习题 三、随堂练习 (由学生演示) |









