

北京市门头沟区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
展开北京市门头沟区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
一.动点问题的函数图象(共2小题)
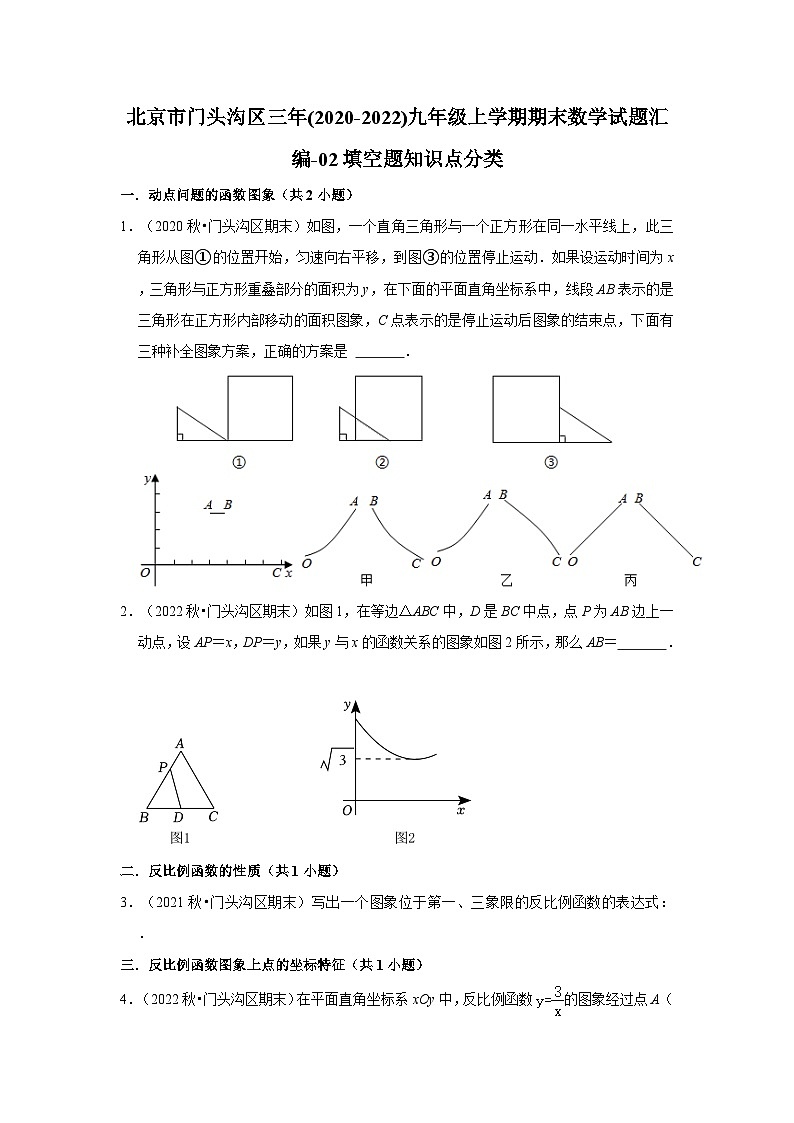
1.(2020秋•门头沟区期末)如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,三角形与正方形重叠部分的面积为y,在下面的平面直角坐标系中,线段AB表示的是三角形在正方形内部移动的面积图象,C点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .
2.(2022秋•门头沟区期末)如图1,在等边△ABC中,D是BC中点,点P为AB边上一动点,设AP=x,DP=y,如果y与x的函数关系的图象如图2所示,那么AB= .
二.反比例函数的性质(共1小题)
3.(2021秋•门头沟区期末)写出一个图象位于第一、三象限的反比例函数的表达式: .
三.反比例函数图象上点的坐标特征(共1小题)
4.(2022秋•门头沟区期末)在平面直角坐标系xOy中,反比例函数的图象经过点A(1,y1),B(3,y2),那么y1与y2的大小关系是y1 y2(填“>”,“=”或“<”).
四.二次函数的性质(共3小题)
5.(2020秋•门头沟区期末)如果一个二次函数图象开口向下,对称轴为x=1,则该二次函数表达式可以为 .(任意写出一个符合条件的即可)
6.(2021秋•门头沟区期末)函数y=x2+的图象如图所示,在下列结论中:①该函数自变量x的取值范围是x≠0;②该函数有最小值;③方程x2+=3有三个根;④如果(x1,y1)和(x2,y2)是该函数图象上的两个点,当x1<x2<0时一定有y1<y2,所有正确结论的序号是 .
7.(2022秋•门头沟区期末)写出一个二次函数,其图象满足:
①开口向下;
②当x<0时,y随x的增大而增大.
这个二次函数的表达式可以是 .
五.二次函数图象与几何变换(共1小题)
8.(2020秋•门头沟区期末)抛物线y=2x2沿y轴向上平移3个单位长度后的抛物线的表达式为 .
六.二次函数的三种形式(共1小题)
9.(2021秋•门头沟区期末)把二次函数y=x2﹣2x+3化成y=a(x﹣h)2+k的形式为 .
七.勾股定理的逆定理(共1小题)
10.(2020秋•门头沟区期末)如图所示的网格是正方形网格,则∠CBD+∠ABC= °.(点A,B,C,D是网格线交点)
八.垂径定理的应用(共1小题)
11.(2022秋•门头沟区期末)石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知某公园石拱桥的跨度AB=16米,拱高CD=4米,那么桥拱所在圆的半径OA= 米.
九.三角形的内切圆与内心(共1小题)
12.(2021秋•门头沟区期末)《九章算术》是我国古代的数学名著,书中有这样的一个问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“如图,现有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形所能容纳的最大圆的直径是多少?”
答:该直角三角形所能容纳的最大圆的直径是 步.
一十.正多边形和圆(共2小题)
13.(2020秋•门头沟区期末)正方形的边长是2cm,则其外接圆的半径为 cm.
14.(2021秋•门头沟区期末)颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是 米.
一十一.弧长的计算(共1小题)
15.(2020秋•门头沟区期末)如图,圆心角为120°,半径为4的弧,则这条弧的长度是 .
一十二.扇形面积的计算(共2小题)
16.(2021秋•门头沟区期末)如图,扇形的圆心角∠AOB=60°,半径为3cm.如果点C、D是AB的三等分点,图中所有阴影部分的面积之和是 cm2.
17.(2022秋•门头沟区期末)如果一个扇形的圆心角为90°,半径为2,那么该扇形的面积为 (结果保留π).
一十三.比例的性质(共1小题)
18.(2021秋•门头沟区期末)如果=,那么的值是 .
一十四.相似三角形的性质(共1小题)
19.(2021秋•门头沟区期末)如果两个相似三角形的相似比是1:3,那么这两个相似三角形的周长比是 .
一十五.相似三角形的判定与性质(共2小题)
20.(2020秋•门头沟区期末)如图:在△ABC中,DE∥BC,AD=1,BD=2,则= .
21.(2022秋•门头沟区期末)如图所示的网格是正方形网格,A,B,C,D,E是网格线的交点,那么△ADE的面积与△ABC的面积的比是 .
一十六.相似三角形的应用(共1小题)
22.(2022秋•门头沟区期末)《孙子算经》是中国古代重要的数学著作,其中有首歌谣:“今有竿不知其长,量得影长一百五十寸,立一标杆,长一十五寸,影长五寸,问竿长几何?”.
其意思是:“如图,有一根竹竿AB不知道有多长,量出它在太阳下的影子BC长150寸,同时立一根15寸的小标杆DE,它的影子EF长5寸,则竹竿AB的长为多少?”.
答:竹竿AB的长为 寸.
一十七.锐角三角函数的定义(共1小题)
23.(2020秋•门头沟区期末)在Rt△ABC中,∠C=90°,AB=5,BC=4,则cosA= .
一十八.特殊角的三角函数值(共1小题)
24.(2022秋•门头沟区期末)如果tanα=1,那么锐角α= 度.
北京市门头沟区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类
参考答案与试题解析
一.动点问题的函数图象(共2小题)
1.(2020秋•门头沟区期末)如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,三角形与正方形重叠部分的面积为y,在下面的平面直角坐标系中,线段AB表示的是三角形在正方形内部移动的面积图象,C点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 乙 .
【答案】乙.
【解答】解:设正方形的边长为a,直角三角形的面积为s,
①如图,当三角形从图①的位置开始,匀速向右平移到②的位置时,如图:
设重叠的图形为△DEF,∠DFE=α,
则EF=x,DE=EFtanα=xtanα,
则y=EF×DE=×x•xtanα=tanα•x2,该函数的表达式为开口向上的抛物线,
②当直角三角形在正方形内部时,
则y为常数,即为直角三角形的面积,对应函数图象AB段;
③当三角形通过正方形内部,匀速向右平移到②的位置时,
同理可得:y=s﹣(x﹣a)2•tanα=﹣tanα•x2+a•tanα•x﹣a2tanα+s,该函数的表达式为开口向下的抛物线,
故答案为:乙.
2.(2022秋•门头沟区期末)如图1,在等边△ABC中,D是BC中点,点P为AB边上一动点,设AP=x,DP=y,如果y与x的函数关系的图象如图2所示,那么AB= 4 .
【答案】4.
【解答】解:由图2可得y最小值=,
∵△ABC为等边三角形,分析图1可知,当P点运动到DP⊥AB时,DP长为最小值,
∴此时DP=,
∵∠B=60°,
∴sin60°=,
解得BD=2,
∵D为BC的中点,
∴BC=4,
∴AB=4.
故答案为:4.
二.反比例函数的性质(共1小题)
3.(2021秋•门头沟区期末)写出一个图象位于第一、三象限的反比例函数的表达式: .
【答案】见试题解答内容
【解答】解;设反比例函数解析式为y=,
∵图象位于第一、三象限,
∴k>0,
∴可写解析式为y=,
故答案为:y=.
三.反比例函数图象上点的坐标特征(共1小题)
4.(2022秋•门头沟区期末)在平面直角坐标系xOy中,反比例函数的图象经过点A(1,y1),B(3,y2),那么y1与y2的大小关系是y1 > y2(填“>”,“=”或“<”).
【答案】>.
【解答】解:∵k=3>0,
∴反比例函数的图象在一、三象限,
∴点A(1,y1),B(3,y2)两点在第一象限,
∴y1>y2>0,
∴y1,y2的大小关系为y1>y2.
故答案为:>.
四.二次函数的性质(共3小题)
5.(2020秋•门头沟区期末)如果一个二次函数图象开口向下,对称轴为x=1,则该二次函数表达式可以为 y=﹣(x﹣1)2(答案不唯一) .(任意写出一个符合条件的即可)
【答案】y=﹣(x﹣1)2(答案不唯一).
【解答】解:∵一个二次函数图象开口向下,对称轴为x=1,
∴该函数的解析式可以为y=﹣(x﹣1)2,
故答案为:y=﹣(x﹣1)2(答案不唯一).
6.(2021秋•门头沟区期末)函数y=x2+的图象如图所示,在下列结论中:①该函数自变量x的取值范围是x≠0;②该函数有最小值;③方程x2+=3有三个根;④如果(x1,y1)和(x2,y2)是该函数图象上的两个点,当x1<x2<0时一定有y1<y2,所有正确结论的序号是 ①③ .
【答案】①③.
【解答】解:如图:
①函数y=x2+中,分母不能为0,所以函数自变量x的取值范围是x≠0,故①符合题意.
②如图所示,函数没有最大值,没有最小值,故②不符合题意.
③如图所示,函数y=x2+的图象与直线y=3有3个交点,所以方程x2+=3有三个根,故③符合题意.
④如图所示,当x<0时,y随x的增大而减小,故④不符合题意.
综上所述,正确的结论有①③个.
故答案为:①③.
7.(2022秋•门头沟区期末)写出一个二次函数,其图象满足:
①开口向下;
②当x<0时,y随x的增大而增大.
这个二次函数的表达式可以是 y=﹣x2+x .
【答案】y=﹣x2+x.(答案不唯一)
【解答】解:设y=ax2+bx+c,
∵抛物线开口向下,
∴a<0,
∵x<0时,y随x的增大而增大,
∴抛物线对称轴在y轴右侧,
∴b>0,
∴y=﹣x2+x满足题意,
故答案为:y=﹣x2+x.(答案不唯一)
五.二次函数图象与几何变换(共1小题)
8.(2020秋•门头沟区期末)抛物线y=2x2沿y轴向上平移3个单位长度后的抛物线的表达式为 y=2x2+3 .
【答案】y=2x2+3.
【解答】解:抛物线y=2x2沿y轴向上平移3个单位长度后的抛物线的表达式为y=2x2+3.
故答案为:y=2x2+3.
六.二次函数的三种形式(共1小题)
9.(2021秋•门头沟区期末)把二次函数y=x2﹣2x+3化成y=a(x﹣h)2+k的形式为 y=(x﹣1)2+2 .
【答案】见试题解答内容
【解答】解:y=x2﹣2x+3,
=x2﹣2x+1+2,
=(x﹣1)2+2,
所以,y=(x﹣1)2+2.
故答案为:y=(x﹣1)2+2.
七.勾股定理的逆定理(共1小题)
10.(2020秋•门头沟区期末)如图所示的网格是正方形网格,则∠CBD+∠ABC= 45 °.(点A,B,C,D是网格线交点)
【答案】45.
【解答】解:如图,连接DC并延长到点E,使CE=DC,连接EA、EB,
则BC是ED的垂直平分线,
∴BE=BD==,
∴∠CBD=∠CBE.
∵AE==,AB==,
∴AE2+AB2=2AB2=BE2,
∴△ABE是等腰直角三角形,
∴∠ABE=45°,
∴∠CBD+∠ABC=∠CBE+∠ABC=∠ABE=45°.
故答案为:45.
八.垂径定理的应用(共1小题)
11.(2022秋•门头沟区期末)石拱桥是中国传统桥梁四大基本形式之一,它的主桥拱是圆弧形.如图,已知某公园石拱桥的跨度AB=16米,拱高CD=4米,那么桥拱所在圆的半径OA= 10 米.
【答案】10.
【解答】解:∵OC⊥AB,
∴AD=BD=8米,
设BO=x米,则DO=(x﹣4)米,
在Rt△OBD中,得:BD2+DO2=BO2,
即82+(x﹣4)2=x2,
解得:x=10,
即桥拱所在圆的半径是10米.
故答案为:10.
九.三角形的内切圆与内心(共1小题)
12.(2021秋•门头沟区期末)《九章算术》是我国古代的数学名著,书中有这样的一个问题:“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“如图,现有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形所能容纳的最大圆的直径是多少?”
答:该直角三角形所能容纳的最大圆的直径是 6 步.
【答案】6.
【解答】解:如图:
在Rt△ABC中,AC=8,BC=15,∠ACB=90°,
∴AB===17,
∴S△ABC=AC•BC=×8×15=60,
设内切圆的圆心为O,分别连接圆心和三个切点,及OA、OB、OC,
设内切圆的半径为r,
∴S△ABC=S△AOB+S△BOC+S△AOC=×r(AB+BC+AC)=20r,
∴20r=60,解得r=3,
∴内切圆的直径为6步.
故答案为:6.
一十.正多边形和圆(共2小题)
13.(2020秋•门头沟区期末)正方形的边长是2cm,则其外接圆的半径为 cm.
【答案】.
【解答】解:如图,连接OA,OD,
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴△AOD是等腰直角三角形,
∴OA2+OD2=AD2,即2OA2=22,解得OA=(cm).
故答案为:.
14.(2021秋•门头沟区期末)颐和园是我国现存规模最大,保存最完整的古代皇家园林,它和承德避暑山庄、苏州拙政园、苏州留园并称为中国四大名园.该园有一个六角亭,如果它的地基是半径为2米的正六边形,那么这个地基的周长是 12 米.
【答案】见试题解答内容
【解答】解:如图所示:
∵正六边形的半径为2米,
∴OA=0B=2米,
∴正六边形的中心角∠AOB==60°,
∴△AOB是等边三角形,
∴AB=OA=OB,
∴AB=2米,
∴正六边形的周长为6×2=12(米);
故答案为:12.
一十一.弧长的计算(共1小题)
15.(2020秋•门头沟区期末)如图,圆心角为120°,半径为4的弧,则这条弧的长度是 .
【答案】.
【解答】解:圆心角为120°,半径为4的弧的长度是l==.
故答案为:.
一十二.扇形面积的计算(共2小题)
16.(2021秋•门头沟区期末)如图,扇形的圆心角∠AOB=60°,半径为3cm.如果点C、D是AB的三等分点,图中所有阴影部分的面积之和是 π cm2.
【答案】π.
【解答】解:S扇形OAB==π(cm2),
S阴影=S扇形OAB=×π=π(cm2).
故答案为:π.
17.(2022秋•门头沟区期末)如果一个扇形的圆心角为90°,半径为2,那么该扇形的面积为 π (结果保留π).
【答案】π.
【解答】解:根据题意,扇形的弧长为=π,
S===π.
故答案为:π.
一十三.比例的性质(共1小题)
18.(2021秋•门头沟区期末)如果=,那么的值是 .
【答案】.
【解答】解:由题意设x=2k,y=3k,
∴,
故答案为:.
一十四.相似三角形的性质(共1小题)
19.(2021秋•门头沟区期末)如果两个相似三角形的相似比是1:3,那么这两个相似三角形的周长比是 1:3 .
【答案】1:3.
【解答】解:∵两个相似三角形的相似比是1:3,
∴这两个相似三角形的周长比是1:3,
故答案为:1:3.
一十五.相似三角形的判定与性质(共2小题)
20.(2020秋•门头沟区期末)如图:在△ABC中,DE∥BC,AD=1,BD=2,则= 9 .
【答案】9.
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴=()2=()2=9.
故答案为9.
21.(2022秋•门头沟区期末)如图所示的网格是正方形网格,A,B,C,D,E是网格线的交点,那么△ADE的面积与△ABC的面积的比是 1:4 .
【答案】1:4.
【解答】解:设正方形网格中的每个小正方形的边长都是1,则AD=1,AB=2,
根据勾股定理得AE==2,AC==4,
∴==,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴===,
∴△ADE的面积与△ABC的面积的比是1:4,
故答案为:1:4.
一十六.相似三角形的应用(共1小题)
22.(2022秋•门头沟区期末)《孙子算经》是中国古代重要的数学著作,其中有首歌谣:“今有竿不知其长,量得影长一百五十寸,立一标杆,长一十五寸,影长五寸,问竿长几何?”.
其意思是:“如图,有一根竹竿AB不知道有多长,量出它在太阳下的影子BC长150寸,同时立一根15寸的小标杆DE,它的影子EF长5寸,则竹竿AB的长为多少?”.
答:竹竿AB的长为 450 寸.
【答案】450.
【解答】解:设竹竿AB的长度为x寸,
∵竹竿的影长=150寸,标杆长=15寸,影长=5寸,
∴=,
解得x=450.
答:竹竿AB的长为450寸,
故答案为:450.
一十七.锐角三角函数的定义(共1小题)
23.(2020秋•门头沟区期末)在Rt△ABC中,∠C=90°,AB=5,BC=4,则cosA= .
【答案】见试题解答内容
【解答】解:在Rt△ABC中,∠C=90°,cosA==.
一十八.特殊角的三角函数值(共1小题)
24.(2022秋•门头沟区期末)如果tanα=1,那么锐角α= 45 度.
【答案】45.
【解答】解:∵tanα=1,
∴锐角α=45度.
故答案为:45.
北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类: 这是一份北京市西城区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共24页。试卷主要包含了已知二次函数满足条件,2+2的过程等内容,欢迎下载使用。
北京市通州区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类: 这是一份北京市通州区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共22页。试卷主要包含了图象上一点,如图,A,B,C为⊙O上的点等内容,欢迎下载使用。
北京市密云区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类: 这是一份北京市密云区三年(2020-2022)九年级上学期期末数学试题汇编-02填空题知识点分类,共20页。试卷主要包含了如图,抛物线y=﹣x2+2等内容,欢迎下载使用。












