2022-2023学年福建省华安中学七下数学期末监测模拟试题含答案

2022-2023学年福建省华安中学七下数学期末监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．不能判定一个四边形是平行四边形的条件是（ ）

A．两组对边分别平行 B．一组对边平行，另一组对边相等

C．一组对边平行且相等 D．两组对边分别相等

2．如果一个三角形的三边长分别为6，a，b，且（a+b）（a-b）=36，那么这个三角形的形状为（    ）

A．锐角三角形 B．钝角三角形

C．直角三角形 D．等边三角形

3．估计的结果在（   ）.

A．8至9之间 B．9至10之间 C．10至11之间 D．11至12之间

4．如图，在平行四边形ABCD中，对角线AC与BD相交于点O，AB＝5，AC+BD＝20，则△AOB的周长为（　　）

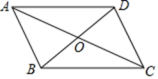
A．10 B．20

C．15 D．25

5．如图，长方形的高为，底面长为 ，宽为，蚂蚁沿长方体表面，从点到（点 见图中黑圆点）的最短距离是（  ）

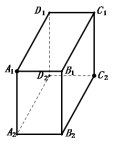
A． B． C． D．

6．如图，在菱形ABCD中，对角线AC，BD相交于点O. 下列结论中不一定成立的是（   ）

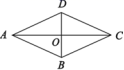
A．AB∥CD B．OA=OC

C．AC⊥BD D．AC=BD

7．若（为整数），则的值可以是（    ）

A．6 B．12 C．18 D．24

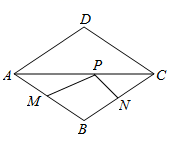
8．如图，点Р是边长为2的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，的最小值是（    ）

A．1 B． C．2 D．

9．使代数式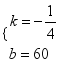的值不小于代数式的值，则应为（    ）

A．＞17 B．≥17 C．＜17 D．≥17

10．某班名学生的身高情况如下表：

则这名学生身高的众数和中位数分别是（  ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．若是关于的方程的一个根，则方程的另一个根是_________.

12．若一组数据1，2，3，x，0，3，2的众数是3，则这组数据的中位数是_____．

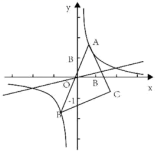
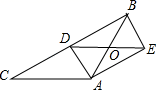
13．如图，在平面直角坐标系xOy中，A是双曲线在第一象限的分支上的一个动点，连接AO并延长与这个双曲线的另一分支交于点B，以AB为底边作等腰直角三角形ABC，使得点C位于第四象限。

（1）点C与原点O的最短距离是________；

（2）没点C的坐标为（，点A在运动的过程中，y随x的变化而变化，y关于x的函数关系式为________。

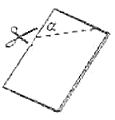
14．如图，把一个正方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为的菱形，剪口与折痕所成的角的度数应为______或______.

15．一次函数y＝﹣x，函数值y随x的增大而_____．

16．如图，在中，，，是的角平分线，过点作于点，若，则___.

三、解下列各题(本大题共8小题，共72分)

17．（8分）先化简，然后从中选出一个合适的整数作为的值代入求值．

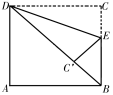
18．（8分）如图，已知正方形ABCD边长为2，E是BC边上一点，将此正方形的一只角DCE沿直线DE折叠，使C点恰好落在对角线BD上，求BE的长.

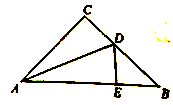
19．（8分）如图，在△ABC中，AB＝AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E．

（1）求证：四边形ADBE是矩形；

（2）连接DE，交AB与点O，若BC＝8，AO＝3，求△ABC的面积．

20．（8分）对于实数a，b，定义运算“⊗”：a⊗b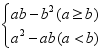＝，例如：5⊗3，因为5＞3，所以5⊗3＝5×3﹣32＝1．若x1，x2是一元二次方程x2﹣3x+2＝0的两个根，则x1⊗x2等于（　　）

A．﹣1 B．±2 C．1 D．±1

21．（8分）类比等腰三角形的定义，我们定义：有三条边相等的凸四边形叫做“准等边四边形”．

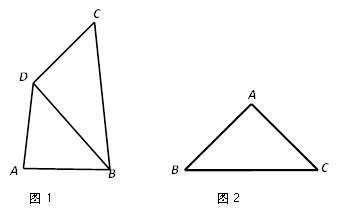
（1）已知：如图1，在“准等边四边形”ABCD中，BC≠AB，BD⊥CD，AB=3，BD=4，求BC的长；

（2）在探究性质时，小明发现一个结论：对角线互相垂直的“准等边四边形”是菱形．请你判断此结论是否正确，若正确，请说明理由；若不正确，请举出反例；

（3）如图2，在△ABC中，AB=AC=，∠BAC=90°．在AB的垂直平分线上是否存在点P，使得以A，B，C，P为顶点的四边形为“准等边四边形”． 若存在，请求出该“准等边四边形”的面积；若不存在，请说明理由．

22．（10分）甲、乙两名射击运动员进行射击比赛，两人在相同的条件下各射击10次，射击的成绩如图所示．根据图中信息，解答下列问题：

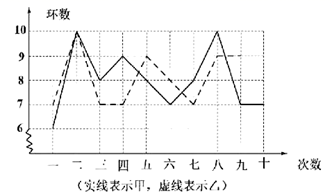
（1）算出乙射击成绩的平均数；

（2）经计算，甲射击成绩的平均数为8，乙射击成绩的方差为1.2，请你计算出甲射击成绩的方差，并判断谁的射击成绩更加稳定．

23．（10分）阅读材料：分解因式：x2+2x-3

解：原式=x2+2x+1-4=（x+1）2-4

=（x+1+2）（x+1-2）=（x+3）（x-1）

此种方法抓住了二次项和一次项的特点，然后加一项，使这三项成为完全平方式，我们把这种分解因式的方法叫配方法．请仔细体会配方法的特点，然后尝试用配方法解决下列问题：

（1）分解因式x2-2x-3=_______；a2-4ab-5b2=_______；

（2）无论m取何值，代数式m2+6m+13总有一个最小值，请你尝试用配方法求出它的最小值；

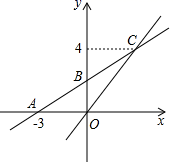
24．（12分）如图，在平面直角坐标系中，一次函数y＝kx+b的图象与x轴交点为A（﹣3，0），与y轴交点为B，且与正比例函数y＝x的图象交于点C（m，4）

（1）求m的值及一次函数y＝kx+b的表达式；

（2）观察函数图象，直接写出关于x的不等式x≤kx+b的解集；

（3）若P是y轴上一点，且△PBC的面积是8，直接写出点P的坐标．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、C

3、C

4、C

5、D

6、D

7、C

8、C

9、B

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、1

13、       

14、       

15、减小

16、

三、解下列各题(本大题共8小题，共72分)

17、-1

18、BE=.

19、（1）详见解析；（2）8

20、D

21、（1）5；（2）正确，证明详见解析；（3）存在，有四种情况，面积分别是：，，，

22、（1）8；（2）乙.

23、（1）（x-3）（x+1）；（a+b）（a-5b）;（2）代数式m2+6m+13的最小值是1

24、（1）y＝x+2；（2）x≤3；（3）P 的坐标为（0，）或（0，﹣）.