


2022-2023学年浙江省衢州市六校联谊七年级数学第二学期期末联考模拟试题含答案
展开2022-2023学年浙江省衢州市六校联谊七年级数学第二学期期末联考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.已知一次函数y=kx+2,y随x的增大而增大,则该函数的图象一定经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
2.最早记载勾股定理的我国古代数学名著是( )
A.《九章算术》 B.《周髀算经》 C.《孙子算经》 D.《海岛算经》
3.(2016山西省)宽与长的比是![]() (约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
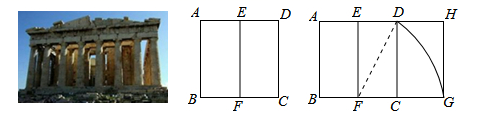
A.矩形ABFE B.矩形EFCD C.矩形EFGH D.矩形DCGH
4.将直线![]() 向下平移2个单位,得到直线( )
向下平移2个单位,得到直线( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在平面直角坐标系中,点M(3,2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图像可以表示为中的( )
A.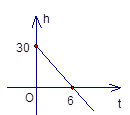 B.
B. C.
C.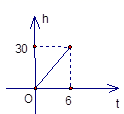 D.
D.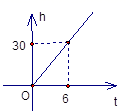
7.下列各式:![]() ,其中分式共有( )
,其中分式共有( )
A.2 个 B.3 个 C.4 个 D.5 个
8.函数![]() 与
与![]() 在同一坐标系内的图像可能是( )
在同一坐标系内的图像可能是( )
A.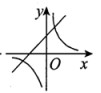 B.
B.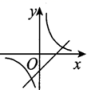
C.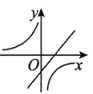 D.
D.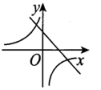
9.如图,![]() ABC中,∠ACB=90°,∠ABC=22.5°,将
ABC中,∠ACB=90°,∠ABC=22.5°,将![]() ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
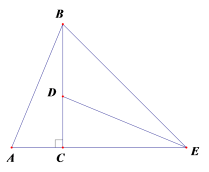
①DE⊥AB ②∠BCE是旋转角 ③∠BED=30° ④![]() BDE与
BDE与![]() CDE面积之比是
CDE面积之比是![]() :1
:1
A.1个 B.2个 C.3个 D.4个
10.已知四边形 ABCD ,有以下四个条件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .从这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法有( )
A.3 种 B.4 种 C.5 种 D.6 种
二、填空题(本大题共有6小题,每小题3分,共18分)
11.正五边形的内角和等于______度.
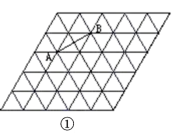
12.图中的虚线网格是等边三角形,它的每一个小三角形都是边长为1的等边三角形.
(1)如图①,连接相邻两个小正三角形的顶点A,B,则AB的长为_______
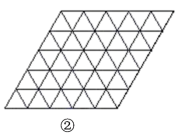
(2)在如图②所示的网格中,用无刻度的直尺,画一个斜边长为![]() 的直角三角形,且它的顶点都在格点上.
的直角三角形,且它的顶点都在格点上.
13.现有两根木棒的长度分别是4 米和3 米,若要钉成一个直角三角形木架,则第三根木棒的长度为_________米.
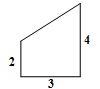
14.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、3、4,则原直角三角形纸片的斜边长是 .
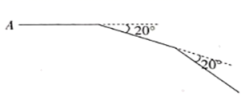
15.如图,小明从点![]() 出发,前进5
出发,前进5 ![]() 后向右转20°,再前进5
后向右转20°,再前进5 ![]() 后又向右转20°,这样一直走下去,直到他第一次回到出发点
后又向右转20°,这样一直走下去,直到他第一次回到出发点![]() 为止,他所走的路径构成了一个多边形
为止,他所走的路径构成了一个多边形
(1)小明一共走了________米;
(2)这个多边形的内角和是_________度.
16.当x=4时,二次根式![]() 的值为______.
的值为______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)计算:(1)分解因式:m2(x﹣y)+4n2(y﹣x);
(2)解不等式组![]() ,并把解集在数轴上表示出来;
,并把解集在数轴上表示出来;
(3)先化简,再求解, ![]() ,其中x=
,其中x=![]() ﹣2.
﹣2.
18.(8分)在平面直角坐标系中,如果点P 的横坐标和纵坐标相等,则称点P为和谐点。
(1)求函数![]() 的图像上和谐点的坐标;
的图像上和谐点的坐标;
(2)若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点(![]() ,
,![]() ),当0≤x≤m时,函数y=ax2+4x+c﹣
),当0≤x≤m时,函数y=ax2+4x+c﹣![]() (a≠0)的最小值为﹣3,最大值为1,则m的取值范围.
(a≠0)的最小值为﹣3,最大值为1,则m的取值范围.
19.(8分)申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:
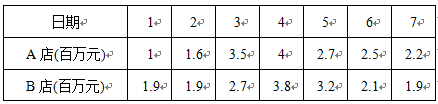
(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;
(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1)
(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.
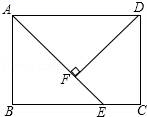
20.(8分)如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.
21.(8分)四张扑克牌的牌面如图①所示,将扑克牌洗均匀后,如图②背面朝上放置在桌面上。

(1)若随机抽取一张扑克牌,则牌面数字恰好为5的概率是_____________;
(2)规定游戏规则如下:若同时随机抽取两张扑克牌,抽到两张牌的牌面数字之和是偶数为胜;反之,则为负。你认为这个游戏是否公平?请说明理由。
22.(10分)如图,在平面直角坐标系中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象都经过点
的图象都经过点![]() .
.
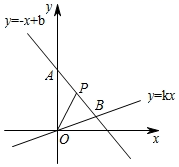
(1)求一次函数和正比例函数的解析式;
(2)若点![]() 是线段
是线段![]() 上一点,且在第一象限内,连接
上一点,且在第一象限内,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于
关于![]() 的函数解析式.
的函数解析式.
23.(10分)(1)![]() ;
;
(2)![]() .
.
24.(12分)某车行经销的A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
今年A,B两种型号车的进价和售价如下表:
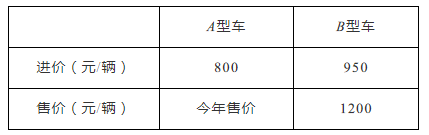
(1)求今年A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆,应如何进货才能使这批车售完后获利最多?
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、D
4、A
5、A
6、B
7、A
8、B
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、540
12、 (1)![]() ;(2)见解析.
;(2)见解析.
13、![]() .
.
14、2![]() 或10.
或10.
15、90 2880
16、0
三、解下列各题(本大题共8小题,共72分)
17、(1)(x﹣y)(m+2n)(m-2n);(2)![]() ,见解析;(3)4
,见解析;(3)4![]() -6.
-6.
18、(1)![]() ;(2)2≤m≤4
;(2)2≤m≤4
19、(1)选择平均数,A店的日营业额的平均值是2.5百万元,B店的日营业额的平均值是2.5百万元;(2)A组新数据的方差约为1.1,B组新数据的方差约为1.6;(3)答案见解析.
20、见解析
21、(1)![]() (2)不公平.获胜
(2)不公平.获胜![]() ,否则
,否则![]() .
.
22、(1)y=﹣x+4,![]() ;(2)S=2x(0<x≤3).
;(2)S=2x(0<x≤3).
23、(1)![]() ;(2)
;(2)![]() .
.
24、(1)![]() 型车每辆售价为1000元;(2)
型车每辆售价为1000元;(2)![]() 型车30辆、
型车30辆、![]() 型车20辆,获利最多.
型车20辆,获利最多.
浙江省衢州市六校联谊2023-2024学年九年级数学第一学期期末质量跟踪监视模拟试题含答案: 这是一份浙江省衢州市六校联谊2023-2024学年九年级数学第一学期期末质量跟踪监视模拟试题含答案,共9页。试卷主要包含了考生必须保证答题卡的整洁,已知关于的方程个等内容,欢迎下载使用。
浙江省衢州市六校联谊2023-2024学年八年级数学第一学期期末达标测试试题含答案: 这是一份浙江省衢州市六校联谊2023-2024学年八年级数学第一学期期末达标测试试题含答案,共7页。试卷主要包含了下列因式分解中,下列运算正确的是等内容,欢迎下载使用。
浙江省海曙区五校联考2022-2023学年七年级数学第二学期期末联考模拟试题含答案: 这是一份浙江省海曙区五校联考2022-2023学年七年级数学第二学期期末联考模拟试题含答案,共6页。试卷主要包含了下列式子中属于最简二次根式的是等内容,欢迎下载使用。












