2022-2023学年河南省郑州一中数学七下期末预测试题含答案

2022-2023学年河南省郑州一中数学七下期末预测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（　　）

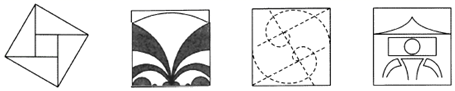
A．1个 B．2个 C．3个 D．4个

2．如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A，则不等式0＜kx+b＜2x的解集为（　　）

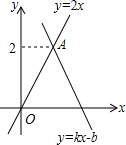
A． B． C． D．

3．下列二次根式中，化简后能与合并的是　　

A． B． C． D．

4．当时，函数的值是（     ）

A．-3 B．-5 C．-7 D．-9

5．一次函数的图像不经过第四象限，那么的取值范围是（    ）

A． B． C． D．

6．如图，△ABC的周长为28，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝12，则PQ的长为（　　）

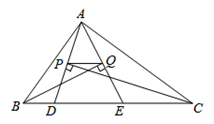
A．1 B．2 C．3 D．4

7．在一次函数y＝kx+1中，若y随x的增大而增大，则它的图象不经过第（　　）象限

A．四    B．三    C．二    D．一

8．在平行四边形ABCD中，若∠B=135°，则∠D=（    ）

A．45° B．55° C．135° D．145°

9．甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，他们分别以不同的速度匀速行驶.已知甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示，当乙到达终点A时，甲还需(   )分钟到达终点B．

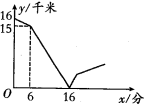
A．78 B．76 C．16 D．12

10．已知一次函数y1=2x+m与y2=2x+n（m≠n）的图象如图所示，则关于x与y的二元一次方程组 的解的个数为（   ）

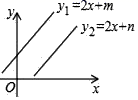
A．0个 B．1个 C．2个 D．无数个

二、填空题(本大题共有6小题，每小题3分，共18分)

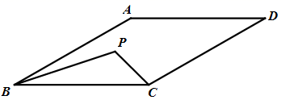
11．如图，边长为4的菱形ABCD中，∠ABC＝30°，P为BC上方一点，且，则PB＋PC的最小值为___________．

12．某学习小组有5人，在一次数学测验中的成绩分别是102, 106, 100, 105, 102,则他们成绩的平均数_______________

13．现有一张矩形纸片ABCD（如图），其中AB=4cm，BC=6cm，点E是BC的中点．将纸片沿直线AE折叠，点B落在四边形AECD内，记为点B′．则线段B′C=           ．

14．当x______时，分式有意义.

15．将一次函数y＝﹣x+1沿x轴方向向右平移3个单位长度得到的直线解析式为_____．

16．在平面直角坐标系xOy中，直线与x，y轴分别交于点A，B，若将该直线向右平移5个单位，线段AB扫过区域的边界恰好为菱形，则k的值为_____.

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF，

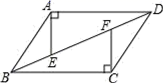
求证：四边形ABCD是平行四边形．

18．（8分）9月28日，我国神舟七号载人飞船顺利返回地面，下面是“神舟”七号飞船返回舱返回过程中的相关记录：从返回舱制动点火至减速伞打开期间，返回舱距离地面的高度与时间呈二次函数关系，减速伞打开后，返回舱距离地面的高度与时间呈一次函数关系，高度和时间的对应关系如下表：

1.                                        设减速伞打开后x分钟，返回舱距离地面的高度为hkm，求h与x的函数关系式。
2.                                        在返回舱在距离地面5km时，要求宇航员打开电磁信号灯以便地面人员搜寻，判断宇航员应在何时开启信号灯？

19．（8分）老师随机抽査了本学期学生读课外书册数的情况，绘制成不完整的条形统计图和不完整的扇形统计图（如图所示）．

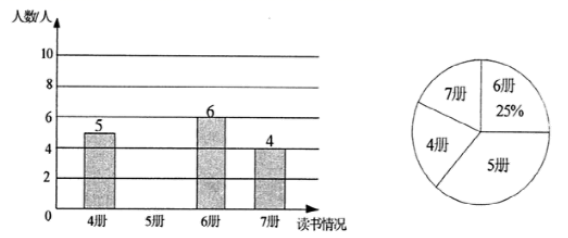
（1）补全条形统计图；

（2）求出扇形统计图中册数为4的扇形的圆心角的度数；

（3）老师随后又补查了另外几人，得知最少的读了6册，将其与之前的数据合并后发现册数的中位数没改变，则最多补查了　   　．

20．（8分）为缓解油价上涨给出租车待业带来的成本压力，某巿自2018年11月17日起，调整出租车运价，调整方案见下列表格及图象（其中a，b，c为常数）

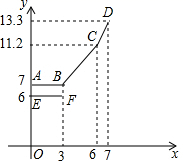
设行驶路程xkm时，调价前的运价y1（元），调价后的运价为y2（元）如图，折线ABCD表示y2与x之间的函数关系式，线段EF表示当0≤x≤3时，y1与x的函数关系式，根据图表信息，完成下列各题：

（1）填空：a=　   　，b=　   　，c=　   　．

（2）写出当x＞3时，y1与x的关系，并在上图中画出该函数的图象．

（3）函数y1与y2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义，若不存在请说明理由．

21．（8分）某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产、两种产品共50件.已知生产一件种产品需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件种产品需用甲种原料4千克、乙种原料10千克，可获利润1200元.设生产种产品的件数为（件），生产、两种产品所获总利润为（元）

（1）试写出与之间的函数关系式：

（2）求出自变量的取值范围；

（3）利用函数的性质说明哪种生产方案获总利润最大？最大利润是多少？

22．（10分）（如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．

⑴如图②，若M为AD边的中点，①△AEM的周长=_________cm；②求证：EP=AE+DP；

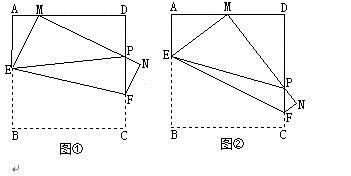
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．

23．（10分）阅读材料：

关于的方程：

的解为：，

（可变形为）的解为：，

的解为：，

的解为：，

…………

根据以上材料解答下列问题：

（1）①方程的解为           ．

②方程的解为           ．

（2）解关于方程：

①  （）

②（）

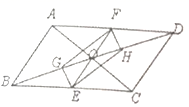
24．（12分）如图，的对角线相交于点，直线EF过点O分别交BC，AD于点E、F，G、H分别为OB、OD的中点，求证：四边形GEHF是平行四边形．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、A

3、B

4、C

5、A

6、B

7、A

8、C

9、A

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、103

13、.

14、≠

15、

16、

三、解下列各题(本大题共8小题，共72分)

17、见解析.

18、（1）h=-2x+20   (2)5时25分30秒(或减速伞打开后7.5秒)

19、（1）见解析（2）75°（3）3人

20、（1）7，1.4，2.1；（2）y1=2.1x﹣0.3；图象见解析；（3）函数y1与y2的图象存在交点（，9）；其意义为当 x<时是方案调价前合算，当x>时方案调价后合算．

21、（1）y与x之间的函数关系式是；

（2）自变量x的取值范围是x = 30，31，1；

（3）生产A种产品 30件时总利润最大，最大利润是2元，

22、（1）①6 ，②见解析；（2）△PDM的周长保持不变，理由见解析.

23、（1）①，；②，；（2）①，；②，．

24、见解析.