


2022-2023学年江苏省泰兴市西城初级中学七下数学期末质量检测试题含答案
展开
这是一份2022-2023学年江苏省泰兴市西城初级中学七下数学期末质量检测试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
2022-2023学年江苏省泰兴市西城初级中学七下数学期末质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下面四个多项式中,能进行因式分解的是( )A.x2+y2 B.x2﹣y C.x2﹣1 D.x2+x+12.已知x=![]() +1,y=
+1,y=![]() -1,则
-1,则![]() 的值为( )A.20 B.16 C.2
的值为( )A.20 B.16 C.2![]() D.4
D.4![]() 3.某小区居民利用“健步行APP”开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步数
3.某小区居民利用“健步行APP”开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步数![]() 单位:千步
单位:千步![]() ,并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.
,并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.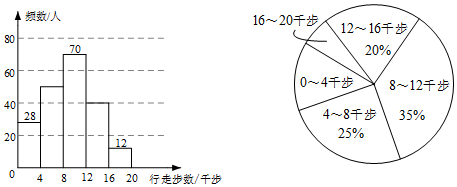 有下面四个推断:
有下面四个推断:![]() 小文此次一共调查了200位小区居民;
小文此次一共调查了200位小区居民;![]() 行走步数为
行走步数为![]() 千步的人数超过调查总人数的一半;
千步的人数超过调查总人数的一半;![]() 行走步数为
行走步数为![]() 千步的人数为50人;
千步的人数为50人;![]() 行走步数为
行走步数为![]() 千步的扇形圆心角是
千步的扇形圆心角是![]() .根据统计图提供的信息,上述推断合理的是( )A.
.根据统计图提供的信息,上述推断合理的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.一元一次不等式组
4.一元一次不等式组![]() 的解集为x>a,则a与b的关系为( )A.a>b B.a<b C.a≥b D.a≤b5.如图,在正方形
的解集为x>a,则a与b的关系为( )A.a>b B.a<b C.a≥b D.a≤b5.如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .下列结论:①
.下列结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 为等边三角形;④当
为等边三角形;④当![]() 时,
时,![]() .其中正确的结论是( )
.其中正确的结论是( )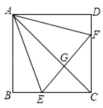 A.①③ B.②④ C.①③④ D.②③④6.若分式
A.①③ B.②④ C.①③④ D.②③④6.若分式![]() 有意义,则实数
有意义,则实数![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.等腰三角形的周长为20,设底边长为
7.等腰三角形的周长为20,设底边长为![]() ,腰长为
,腰长为![]() ,则
,则![]() 关于
关于![]() 的函数解析式为(
的函数解析式为(![]() 为自变量)( )A.
为自变量)( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.下面哪个点不在函数y=-2x+3的图象上( )A.(-5,13) B.(0.5,2) C.(1,2) D.(1,1)9.如图,将
8.下面哪个点不在函数y=-2x+3的图象上( )A.(-5,13) B.(0.5,2) C.(1,2) D.(1,1)9.如图,将![]() 个全等的阴影小正方形摆放得到边长为
个全等的阴影小正方形摆放得到边长为![]() 的正方形
的正方形![]() ,中间小正方形的各边的中点恰好为另外
,中间小正方形的各边的中点恰好为另外![]() 个小正方形的一个顶点,小正方形的边长为
个小正方形的一个顶点,小正方形的边长为![]() (
(![]() 、
、![]() 为正整数),则
为正整数),则![]() 的值为( )
的值为( ) A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.甲安装队为 A小区安装
10.甲安装队为 A小区安装 ![]() 台空调,乙安装队为 B小区安装
台空调,乙安装队为 B小区安装 ![]() 台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装
台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装 ![]() 台,设乙队每天安装
台,设乙队每天安装 ![]() 台,根据题意,下面所列方程中正确的是
台,根据题意,下面所列方程中正确的是 ![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.正方形具有而菱形不一定具有的性质是( )A.四边相等 B.对角线相等 C.对角线互相垂直 D.对角线互相平分12.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )A.
11.正方形具有而菱形不一定具有的性质是( )A.四边相等 B.对角线相等 C.对角线互相垂直 D.对角线互相平分12.一次函数y=kx+b,当k<0,b<0时,它的图象大致为( )A.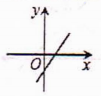 B.
B.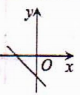 C.
C.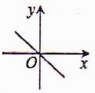 D.
D.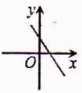 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____.
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图,在矩形ABCD中,AB=5,AD=9,点P为AD边上点,沿BP折叠△ABP,点A的对应点为E,若点E到矩形两条较长边的距离之比为1:4,则AP的长为_____. 14.对于一个函数,如果它的自变量 x 与函数值 y 满足:当−1≤x≤1 时,−1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=−x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,−1)和点 B(−1,1),则 a 的取值范围是______________.15. “对顶角相等”的逆命题是________命题(填真或假)16.如图,Rt△
14.对于一个函数,如果它的自变量 x 与函数值 y 满足:当−1≤x≤1 时,−1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=−x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,−1)和点 B(−1,1),则 a 的取值范围是______________.15. “对顶角相等”的逆命题是________命题(填真或假)16.如图,Rt△![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长是________.
的长是________.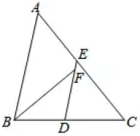 17.已知一次函数y=mx+n(m≠0,m,n为常数),x与y的对应值如下表:x﹣2﹣10123y﹣101234那么,不等式mx+n<0的解集是_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
17.已知一次函数y=mx+n(m≠0,m,n为常数),x与y的对应值如下表:x﹣2﹣10123y﹣101234那么,不等式mx+n<0的解集是_____.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.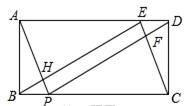 (1)断⊿BEC的形状,并说明理由;(2)判断四边形EFPH是什么特殊四边形?并证明你的判断. 19.(5分)如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.
(1)断⊿BEC的形状,并说明理由;(2)判断四边形EFPH是什么特殊四边形?并证明你的判断. 19.(5分)如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.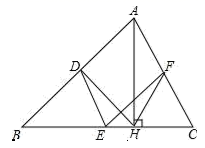 20.(8分)下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:考试类别平时考试期中考试期末考试第一单元第二单元第三单元第四单元成绩(分)857890919094(1)小明6次成绩的众数是 ,中位数是 ;(2)求该同学这个同学这一学期平时成绩的平均数;(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分? 21.(10分)(1)计算:(-1)2019-|-4|+(3.14-π)0+(
20.(8分)下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:考试类别平时考试期中考试期末考试第一单元第二单元第三单元第四单元成绩(分)857890919094(1)小明6次成绩的众数是 ,中位数是 ;(2)求该同学这个同学这一学期平时成绩的平均数;(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分? 21.(10分)(1)计算:(-1)2019-|-4|+(3.14-π)0+(![]() )-1(2)先化简,再求值:(1-
)-1(2)先化简,再求值:(1-![]() )÷
)÷![]() ,再从-1,0,1和2中选一个你认为合适的数作为x的值代入求值. 22.(10分)(1)问题发现.如图1,
,再从-1,0,1和2中选一个你认为合适的数作为x的值代入求值. 22.(10分)(1)问题发现.如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 、
、![]() 、
、![]() 均在同一直线上,连接
均在同一直线上,连接![]() .
.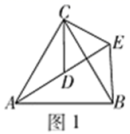 ①求证:
①求证:![]() .②求
.②求![]() 的度数.③线段
的度数.③线段![]() 、
、![]() 之间的数量关系为__________.(2)拓展探究.如图2,
之间的数量关系为__________.(2)拓展探究.如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() .
.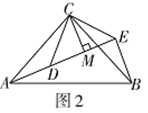 ①请判断
①请判断![]() 的度数为____________.②线段
的度数为____________.②线段![]() 、
、![]() 、
、![]() 之间的数量关系为________.(直接写出结论,不需证明) 23.(12分)如图,△ABC中,∠B=90°,AB=3,BC=4,CD=12,AD=13,点E是AD的中点,求CE的长.
之间的数量关系为________.(直接写出结论,不需证明) 23.(12分)如图,△ABC中,∠B=90°,AB=3,BC=4,CD=12,AD=13,点E是AD的中点,求CE的长.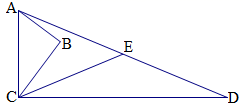 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、C4、C5、A6、B7、C8、C9、B10、D11、B12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、C2、A3、C4、C5、A6、B7、C8、C9、B10、D11、B12、B 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、![]() 14、
14、![]() 或
或![]() 15、假16、1;17、x<﹣1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)△BEC是直角三角形,理由见解析;(2)四边形EFPH为矩形,证明见解析;19、(1)见解析;(2)70°.20、(1)90分;90分;(2)86分;(3)91.2分.21、(1)-1;(2)x=-1时,原式=
15、假16、1;17、x<﹣1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)△BEC是直角三角形,理由见解析;(2)四边形EFPH为矩形,证明见解析;19、(1)见解析;(2)70°.20、(1)90分;90分;(2)86分;(3)91.2分.21、(1)-1;(2)x=-1时,原式=![]() .22、(1)①详见解析;②60°;③
.22、(1)①详见解析;②60°;③![]() ;(2)①90°;②
;(2)①90°;②![]() 23、6.5
23、6.5
相关试卷
这是一份2023-2024学年江苏省泰兴市西城初级中学九上数学期末经典试题含答案,共9页。试卷主要包含了考生必须保证答题卡的整洁,如图,的直径,弦于,如图, 在同一坐标系中等内容,欢迎下载使用。
这是一份2023-2024学年江苏省泰兴市西城初级中学数学八上期末学业质量监测模拟试题含答案,共8页。试卷主要包含了下列分式不是最简分式的是,如果点P,能使分式的值为零的所有x的值是等内容,欢迎下载使用。
这是一份2022-2023学年泰兴市济川中学七下数学期末质量检测试题含答案,共7页。









