


2021届江苏省苏州市相城区高三第一学期阶段性诊断测试数学试卷(word版,含答案)
展开苏州相城区2020-2021学年高三第一学期阶段性诊断测试
数学试卷
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题-卡和试卷指定位置上;
2.本试卷满分150分,考试时间120分钟;
3.答案一律填涂在答题卡上,写在试卷上无效。
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1.设集合A= {x|1≤x≤3}, B= {x|2<x<4}, 则A∩B=( )
A. {x|2<x≤3} B. {x|2≤x≤3} C. {x|1≤x<4} D. {x|1<x<4}
2.命题“![]() 的否定是( )
的否定是( )
A.∀x>2, x2-4≤0 B.∀x≤2, x2-4≤0
C.∃x> 2,![]() D.
D.![]()
3.设![]() 则a, b, c的大小关系为( )
则a, b, c的大小关系为( )
A. a<b<c B. a<c<b C. b<a<c D. b<c<a
4.《算数书》是我国现存最早的有系统的数学典籍,其中记载有求“困盖”的术:置如其周,令相乘也,叉以高乘之,三十六成一。该术相当于给出了由圆锥的底面周长L与h,计算其体积V的近似公式![]() 它实际上是将圆锥体积公式中的圆周率π近似取为3.若圆锥体积的近似公式
它实际上是将圆锥体积公式中的圆周率π近似取为3.若圆锥体积的近似公式![]() 则π应近似取为( )
则π应近似取为( )
![]()
![]()
![]()
![]()
5. 已知函数f![]() 则
则![]()
A.0 ![]() C.1 D.2
C.1 D.2
6.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是![]() 经过一定时间t min的温度是T℃,则
经过一定时间t min的温度是T℃,则![]() 其中
其中![]() (单位:℃)表示环境温度,h(单位:min)称为半衰期。现有一份88℃的热饮,放在24°C的房间中,如果热饮降温到40°C需要20min,那么降温到32°C时,需要的时间为( )min.
(单位:℃)表示环境温度,h(单位:min)称为半衰期。现有一份88℃的热饮,放在24°C的房间中,如果热饮降温到40°C需要20min,那么降温到32°C时,需要的时间为( )min.
A.24 B.25 C.30 D.40
7.已知函数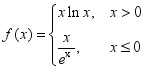 ,则函数y= f(1-x)的图象大致是( )
,则函数y= f(1-x)的图象大致是( )
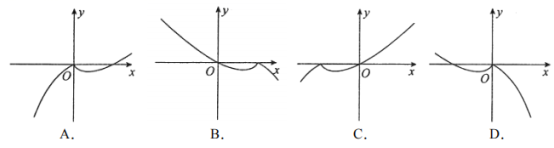
8.若定义在R的奇函数f(x)在(-∞,0)单调递增,且f(2)=0, 则满足xf(x+1)≤0的x的取值范围是()
A. [-3,-1]∪[1,+∞) B. [-3,-1]∪[0,1]
C. (-∞,-3]∪[-1,0]∪[1,+∞) D. [-1,0]∪[1,3]
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得3分,有选错的得0分。
9.某企业2019年12个月的收入与支出数据的折线图如下:
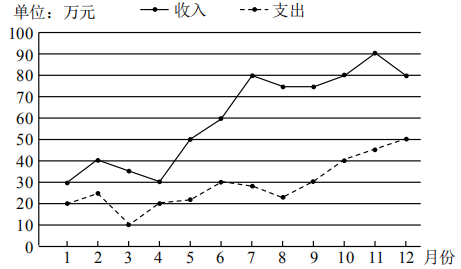
已知:利润=收入-支出,根据该折线图,下列说法正确的是( )
A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润
B.该企业2019年第一季度的利润约是50万元
C.该企业2019年4月至7月的月利润持续增长
D.该企业2019年11月份的月利润最大
10. 下列函数中,当![]() 时,使得
时,使得![]() 恒成立的函数有()
恒成立的函数有()
![]()
![]()
![]()
![]()
11.已知a>0, b>0, 且a+b=2,则下列结论正确的有( )
![]()
![]()
![]()
![]()
12.把方程![]() 1表示的曲线作为函数y= f(x)的图象,则下列结论正确的有( )
1表示的曲线作为函数y= f(x)的图象,则下列结论正确的有( )
A.函数f(x)的图象不经过第三象限
B.函数f(x)在R上单调递增
C.函数f(x)的图象上的点到坐标原点的距离的最小值为1
D.函数g(x)=2f(x)+x不存在零点
三、填空题:本题共4小题,每小题5分,共20分。
13. 关于x的方程![]() )有两个不等实根,一个大于1,一个小于1,则实数m的取值范围为
)有两个不等实根,一个大于1,一个小于1,则实数m的取值范围为![]() ____.
____.
14.已知一个圆柱的轴截面是周长为12米的长方形,则满足这个条件的圆柱的最大体积是___ 立方米。
15.设点P是曲线![]() 上任一点,则点P到直线x-y= 0的最小距离为_______.
上任一点,则点P到直线x-y= 0的最小距离为_______.
16.函数![]() 若方程f(x)=-x+ m有且只有两个不相等的实数根,则实数m的取值范围是___.
若方程f(x)=-x+ m有且只有两个不相等的实数根,则实数m的取值范围是___.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. (本小题满分10分)已知函数![]() 的定义域是集合A,函数
的定义域是集合A,函数![]() 的值域是集合B.
的值域是集合B.
(1)若a=1,求集合A;
(2)若x∈A是x∈B的充分不必要条件,求实数a的取值范围.
18. (本小题满分12分)已知函数![]() 0且a≠1).
0且a≠1).
(1)判断并证明函数的奇偶性;
(2)若________, 判断并证明函数的单调性(在①0<a<1,②a>1,这两个条件中任选一个,将题目补充完整,再作判断证明).
注:第(2)小题中,如果选择多个条件分别解答,按第一个解答计分.
19. (本小题满分12分)已知函数![]()
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,1]上的最小值.
20. (本小题满分12分)2020年9月20日,阳澄西湖南隧道相城段主体完工,它是国内首条穿湖双层叠加、超深、超宽隧道.建成后,将极大地方便周边市民的通行.为了保障通行安全,汽车在隧道内行驶时,需要保持适当的安全车距.安全车距d (单位: m )正比于车速v(单位:km/h)的平方与车身长l(单位: m )的积,即![]() (其中k是比例系数)且安全车距不小于半个车身长.经测算,当车速为60km/h时,安全车距为5.76个车身长.
(其中k是比例系数)且安全车距不小于半个车身长.经测算,当车速为60km/h时,安全车距为5.76个车身长.
(1)试求比例系数k的值;
(2)试写出车距d与车速v之间的函数关系式;
(3)交通繁忙时段,应规定车速为多少时,可使隧道的车流量(单位时间内通过的车辆数)最大?
21. (本小题满分12分)已知二次函数![]() 满足f(-2)=0且方程f(x)=x有两个相等实根.
满足f(-2)=0且方程f(x)=x有两个相等实根.
(1)求函数f(x)的解析式;
(2)解不等式![]()
(3)当且仅当x∈[4,m]时,不等式f(x-t)≤x恒成立,试求t, m的值.
22. (本小题满分12分)已知函数![]() 的极大值为
的极大值为![]() 其中e= 2.71828...为自然对数的底数.
其中e= 2.71828...为自然对数的底数.
(1)求实数b的值;
(2)若函数![]() 对任意x∈(0,+∞),不等式g(x)≥af(x)恒成立.
对任意x∈(0,+∞),不等式g(x)≥af(x)恒成立.
(i)求实数a的取值范围;
(ii)证明:![]() .
.








2020-2021学年江苏省苏州市相城区陆慕高级中学高二(下)期中数学试卷: 这是一份2020-2021学年江苏省苏州市相城区陆慕高级中学高二(下)期中数学试卷,共23页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年江苏省苏州市相城区陆慕高级中学高一(下)期中数学试卷: 这是一份2020-2021学年江苏省苏州市相城区陆慕高级中学高一(下)期中数学试卷,共15页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江苏省苏州市高级中学高三上学期12月阶段性检测数学试题(word版): 这是一份2022-2023学年江苏省苏州市高级中学高三上学期12月阶段性检测数学试题(word版),共14页。












