


人教版九年级上册第22章《二次函数》单元测试卷
展开
这是一份人教版九年级上册第22章《二次函数》单元测试卷,共6页。
人教版九年级上册第22章《二次函数》单元测试卷一、选择题(共36分)1.下列函数中,是二次函数的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.抛物线
2.抛物线![]() 的顶点坐标是( )A.
的顶点坐标是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.下列二次函数的图象,对称轴是y轴的二次函数的表达式是( )A.
3.下列二次函数的图象,对称轴是y轴的二次函数的表达式是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.已知抛物线
4.已知抛物线![]() 的开口向下,顶点坐标为
的开口向下,顶点坐标为![]() ,那么该抛物线有( )A.最小值-3 B.最大值-3 C.最小值2 D.最大值25.抛物线①y=2x2;②y=2(x+1)2﹣5;③y=3(x+1)2;④y=(x+1)2﹣5.其中, 形状相同的是( )A.①② B.②③④ C.②④ D.①④6.平行于x轴的直线与抛物线
,那么该抛物线有( )A.最小值-3 B.最大值-3 C.最小值2 D.最大值25.抛物线①y=2x2;②y=2(x+1)2﹣5;③y=3(x+1)2;④y=(x+1)2﹣5.其中, 形状相同的是( )A.①② B.②③④ C.②④ D.①④6.平行于x轴的直线与抛物线![]() 的一个交点坐标为(-1,2),则另一个交点坐标为( )A.(1,2) B.(1,-2) C.(5,2) D.(-1,4)7.已知,二次函数y=ax2+bx+c满足以下三个条件:①
的一个交点坐标为(-1,2),则另一个交点坐标为( )A.(1,2) B.(1,-2) C.(5,2) D.(-1,4)7.已知,二次函数y=ax2+bx+c满足以下三个条件:①![]() >4c,②a﹣b+c<0,③b<c,则它的图象可能是( )A.
>4c,②a﹣b+c<0,③b<c,则它的图象可能是( )A.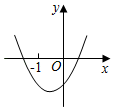 B.
B.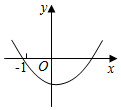 C.
C.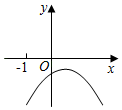 D.
D.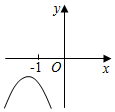 8.若二次函数
8.若二次函数![]() 的图像经过点
的图像经过点![]() 、
、![]() ,则
,则![]() 、
、![]() 的大小关系是( )A.
的大小关系是( )A.![]() B.
B.![]() C.
C.![]() D.不能确定9.已知
D.不能确定9.已知![]() 是非零实数,
是非零实数,![]() ,在同一平面直角坐标系中,二次函数
,在同一平面直角坐标系中,二次函数![]() 与一次函数
与一次函数![]() 的大致图象不可能是( )A.
的大致图象不可能是( )A.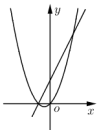 B.
B.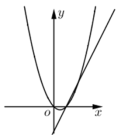 C.
C.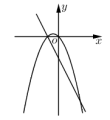 D.
D.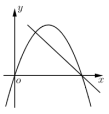 10.长为
10.长为![]() ,宽为
,宽为![]() 的矩形,四个角上剪去边长为
的矩形,四个角上剪去边长为![]() 的小正方形,然后把四边折起来,作成底面为
的小正方形,然后把四边折起来,作成底面为![]() 的无盖的长方体盒子,则y与x的关系式为( )A.
的无盖的长方体盒子,则y与x的关系式为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 11.若二次函数
11.若二次函数![]() ,当
,当![]() 时,y随x的增大而减小,则m的取值范围是( )A.
时,y随x的增大而减小,则m的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 12.一位运动员在距篮筐正下方水平距离
12.一位运动员在距篮筐正下方水平距离![]() 处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为
处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为
,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为![]() ,该运动员身高
,该运动员身高![]() ,在这次跳投中,球在头顶上方
,在这次跳投中,球在头顶上方![]() 处出手,球出手时,他跳离地面的高度是( )
处出手,球出手时,他跳离地面的高度是( )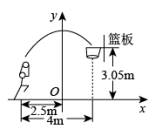 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(共21分)13.请任意写出一个图象开口向下且顶点坐标为(﹣2,1)的二次函数解析式: .14.将二次函数
二、填空题(共21分)13.请任意写出一个图象开口向下且顶点坐标为(﹣2,1)的二次函数解析式: .14.将二次函数![]() 化成
化成![]() 的形式为 .15.将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是 .16.若函数
的形式为 .15.将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是 .16.若函数![]() 的图象与坐标轴有两个不同的交点,则m的值为 .17.如图,抛物线
的图象与坐标轴有两个不同的交点,则m的值为 .17.如图,抛物线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() ,则关于
,则关于![]() 的方程
的方程![]() 的解为 .
的解为 .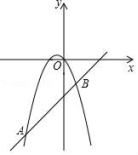 18.已知关于x的二次函数y=ax2﹣6ax+a2﹣8a+3,当﹣1≤x≤2时,有最大值5,则a的值是 .19.已知二次函数
18.已知关于x的二次函数y=ax2﹣6ax+a2﹣8a+3,当﹣1≤x≤2时,有最大值5,则a的值是 .19.已知二次函数 ![]() 的图象如图所示,给出以下结论:①
的图象如图所示,给出以下结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ,其中正确的结论有 .(填序号)
,其中正确的结论有 .(填序号)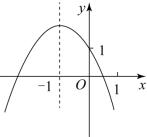 三、解答题(共43分)20.(5分)若二次函数y=ax2+bx+c的图象的顶点是(2,1)且经过点(1,﹣2),求此二次函数解析式. 21.(6分)已知二次函数y=x2﹣4x+3.(1)求该二次函数与x轴的交点坐标和顶点;(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围.
三、解答题(共43分)20.(5分)若二次函数y=ax2+bx+c的图象的顶点是(2,1)且经过点(1,﹣2),求此二次函数解析式. 21.(6分)已知二次函数y=x2﹣4x+3.(1)求该二次函数与x轴的交点坐标和顶点;(2)在所给坐标系中画出该二次函数的大致图象,并写出当y<0时,x的取值范围. 22.(7分)某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);(2)每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元? 23.(8分)如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m),设花圃的宽AB为xm,面积为S
22.(7分)某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=﹣2x+200.为保证市场稳定,供货商规定销售价格不得低于75元/件.(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式(不必写出x的取值范围);(2)每件小电器的销售价格定为多少元时,才能使该款小电器每天获得的利润是1200元? 23.(8分)如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m),设花圃的宽AB为xm,面积为S![]() .(1)求S与x的函数关系式及x值的取值范围;(2)要围成面积为45
.(1)求S与x的函数关系式及x值的取值范围;(2)要围成面积为45![]() 的花圃,AB的长是多少米?(3)当AB的长是多少米时,围成的花圃的面积最大?(结果保留两位小数)
的花圃,AB的长是多少米?(3)当AB的长是多少米时,围成的花圃的面积最大?(结果保留两位小数)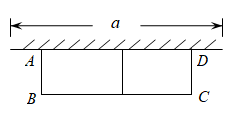 24.(8分)如图,抛物线
24.(8分)如图,抛物线![]() 经过点
经过点![]() ,并与x轴交于点C,点M是抛物线对称轴l上任意一点(点M,B,C三点不在同一直线上).
,并与x轴交于点C,点M是抛物线对称轴l上任意一点(点M,B,C三点不在同一直线上).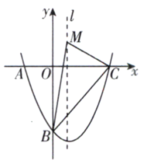 (1)求该抛物线的解析式;(2)在抛物线上找出点P,使得以M,C,B,P为顶点的四边形为平行四边形,并直接写出点P的坐标. 25.(9分)如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(-1,0),与y轴交于点C.
(1)求该抛物线的解析式;(2)在抛物线上找出点P,使得以M,C,B,P为顶点的四边形为平行四边形,并直接写出点P的坐标. 25.(9分)如图,抛物线y=ax2+bx+6与x轴交于点A(6,0),B(-1,0),与y轴交于点C.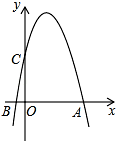 (1)求抛物线的解析式;(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.(3)若抛物线在第一象限的图象上有一点P,求△ACP面积S的最大值.
(1)求抛物线的解析式;(2)若点M为该抛物线对称轴上一点,当CM+BM最小时,求点M的坐标.(3)若抛物线在第一象限的图象上有一点P,求△ACP面积S的最大值.






