人教版2023年九年级上册 第22章《二次函数》单元测试卷
展开
这是一份人教版2023年九年级上册 第22章《二次函数》单元测试卷,共5页。
人教版2023年九年级上册 第22章《二次函数》单元测试卷一.选择题(共10小题,满分30分,每小题3分)1.下列函数中①y=3x+1②y=4x2﹣3x;③y=![]() ④y=﹣2x2+5,是二次函数的有( )A.①② B.②④ C.②③ D.①④2.二次函数y=
④y=﹣2x2+5,是二次函数的有( )A.①② B.②④ C.②③ D.①④2.二次函数y=![]() x2+3x+
x2+3x+![]() 化为y=(x﹣h)2+k的形式,结果正确的是( )A.
化为y=(x﹣h)2+k的形式,结果正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.已知二次函数y=ax2+bx+c的图象过点(1,﹣1),(2,﹣4),(0,4)三点,那么它的对称轴是直线( )A.x=﹣3 B.x=﹣1 C.x=1 D.x=34.已知抛物线y=ax2+bx,当a>0,b<0时,它的图象经过( )A.一,二,三象限 B.一,二,四象限 C.一,三,四象限 D.一,二,三,四象限5.在同一坐标系中,作y=x2,y=﹣
3.已知二次函数y=ax2+bx+c的图象过点(1,﹣1),(2,﹣4),(0,4)三点,那么它的对称轴是直线( )A.x=﹣3 B.x=﹣1 C.x=1 D.x=34.已知抛物线y=ax2+bx,当a>0,b<0时,它的图象经过( )A.一,二,三象限 B.一,二,四象限 C.一,三,四象限 D.一,二,三,四象限5.在同一坐标系中,作y=x2,y=﹣![]() x2,y=
x2,y=![]() x2的图象,它们的共同特点是( )A.抛物线的开口方向向上 B.都是关于x轴对称的抛物线,且y随x的增大而增大 C.都是关于y轴对称的抛物线,且y随x的增大而减小 D.都是关于y轴对称的抛物线,有公共的顶点6.一次函数y=ax+c(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )A.
x2的图象,它们的共同特点是( )A.抛物线的开口方向向上 B.都是关于x轴对称的抛物线,且y随x的增大而增大 C.都是关于y轴对称的抛物线,且y随x的增大而减小 D.都是关于y轴对称的抛物线,有公共的顶点6.一次函数y=ax+c(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )A.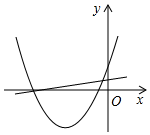 B.
B.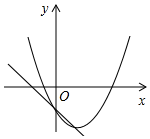 C.
C.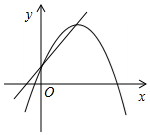 D.
D.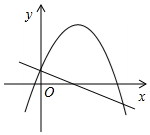 7.当﹣4≤x≤2时,函数y=﹣(x+3)2+2的取值范围为( )A.﹣23≤y≤1 B.﹣23≤y≤2 C.﹣7≤y≤1 D.﹣34≤y≤28.已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )A.k≤4且k≠3 B.k<4且k≠3 C.k<4 D.k≤49.如表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围是( ) x…﹣3﹣2 ﹣1 0 1 … y…﹣11﹣5 ﹣1 1 1 …A.﹣3<x1<﹣2 B.﹣2<x1<﹣1 C.﹣1<x1<0 D.0<x1<110.已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
7.当﹣4≤x≤2时,函数y=﹣(x+3)2+2的取值范围为( )A.﹣23≤y≤1 B.﹣23≤y≤2 C.﹣7≤y≤1 D.﹣34≤y≤28.已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )A.k≤4且k≠3 B.k<4且k≠3 C.k<4 D.k≤49.如表中列出了二次函数y=ax2+bx+c(a≠0)的一些对应值,则一元二次方程ax2+bx+c=0(a≠0)的一个近似解x1的范围是( ) x…﹣3﹣2 ﹣1 0 1 … y…﹣11﹣5 ﹣1 1 1 …A.﹣3<x1<﹣2 B.﹣2<x1<﹣1 C.﹣1<x1<0 D.0<x1<110.已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )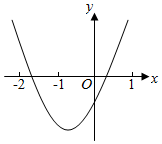 A.4个 B.3个 C.2个 D.1个二.填空题(共8小题,满分32分,每小题4分)11.已知函数y=﹣2x2﹣4x+1,当x 时,y随x的增大而增大.12.二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .13.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是 .(请用“>”连接排序)
A.4个 B.3个 C.2个 D.1个二.填空题(共8小题,满分32分,每小题4分)11.已知函数y=﹣2x2﹣4x+1,当x 时,y随x的增大而增大.12.二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .13.已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是 .(请用“>”连接排序)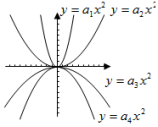 14.抛物线y=x2+6x+m的值恒为正,则m的取值范围 .15.已知二次函数y=x2﹣6x+n的最小值为1,那么n的值是 .16.某超市一月份的营业额为200万元,一月、二月、三月的营业额共y万元,如果平均每月增长率为x,则营业额y与月平均增长率x之间的函数关系式为 .17.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.
14.抛物线y=x2+6x+m的值恒为正,则m的取值范围 .15.已知二次函数y=x2﹣6x+n的最小值为1,那么n的值是 .16.某超市一月份的营业额为200万元,一月、二月、三月的营业额共y万元,如果平均每月增长率为x,则营业额y与月平均增长率x之间的函数关系式为 .17.如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为 米.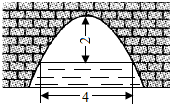 18.对于一个函数,如果它的自变量x与函数值y满足:当﹣1≤x≤1时,﹣1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=﹣x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,﹣1)和点B(﹣1,1),则a的取值范围是 .三.解答题(共7小题,满分58分)19.(6分)根据下列条件求抛物线的解析式:(1)已知抛物线的顶点在原点,且过点(3,18);(2)已知抛物线的顶点坐标为(﹣1,﹣2),且过点(0,﹣3). 20.(6分)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).(1)求抛物线的解析式;(2)求抛物线的对称轴和顶点坐标.
18.对于一个函数,如果它的自变量x与函数值y满足:当﹣1≤x≤1时,﹣1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=﹣x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,﹣1)和点B(﹣1,1),则a的取值范围是 .三.解答题(共7小题,满分58分)19.(6分)根据下列条件求抛物线的解析式:(1)已知抛物线的顶点在原点,且过点(3,18);(2)已知抛物线的顶点坐标为(﹣1,﹣2),且过点(0,﹣3). 20.(6分)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).(1)求抛物线的解析式;(2)求抛物线的对称轴和顶点坐标.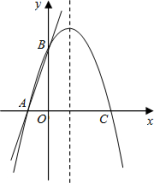 21.(8分)(1)请在坐标系中画出二次函数y=x2﹣2x﹣1的大致图象.(2)根据方程的根与函数图象之间的关系.将方程x2﹣2x﹣1=0的根在图上近似的表示出来;(描点)(3)观察图象,直接写出方程x2﹣2x﹣1=0的根.(精确到0.1)
21.(8分)(1)请在坐标系中画出二次函数y=x2﹣2x﹣1的大致图象.(2)根据方程的根与函数图象之间的关系.将方程x2﹣2x﹣1=0的根在图上近似的表示出来;(描点)(3)观察图象,直接写出方程x2﹣2x﹣1=0的根.(精确到0.1) 22.(8分)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)若设该种品牌玩具的销售单价为x元(x>40),请将销售利润w表示成销售单价x的函数;(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?(3)若想获得最大利润,应将销售价格定为多少,并求出此时的最大利润. 23.(10分)如图所示,二次函数y=﹣2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B.且与y轴交于点C.(1)求m的值及点B的坐标;(2)求△ABC的面积;(3)该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,请求出D点的坐标.
22.(8分)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)若设该种品牌玩具的销售单价为x元(x>40),请将销售利润w表示成销售单价x的函数;(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?(3)若想获得最大利润,应将销售价格定为多少,并求出此时的最大利润. 23.(10分)如图所示,二次函数y=﹣2x2+4x+m的图象与x轴的一个交点为A(3,0),另一个交点为B.且与y轴交于点C.(1)求m的值及点B的坐标;(2)求△ABC的面积;(3)该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,请求出D点的坐标.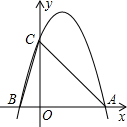 24.(10分)如图,在平面直角坐标系中,直线y=﹣
24.(10分)如图,在平面直角坐标系中,直线y=﹣![]() x﹣2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.(1)求抛物线的解析式;(2)E为抛物线上第一象限部分上一点,当S△ABE=10时,求点E的坐标;(3)F为直线AB下方抛物线上一点,连接AF,当∠FAB=∠BAO时,求F点坐标.
x﹣2与坐标轴分别交于A、B两点,过A、B两点的抛物线解析式为y=x2+bx+c.(1)求抛物线的解析式;(2)E为抛物线上第一象限部分上一点,当S△ABE=10时,求点E的坐标;(3)F为直线AB下方抛物线上一点,连接AF,当∠FAB=∠BAO时,求F点坐标.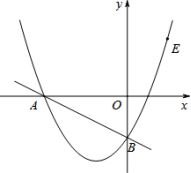 25.(10分)如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式及点B坐标;(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
25.(10分)如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式及点B坐标;(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.