江西省鹰潭市余江区2022-2023学年八年级下学期期中数学试题

这是一份江西省鹰潭市余江区2022-2023学年八年级下学期期中数学试题，共12页。

2022-2023学年度第二学期
八年级数学期中作业题
说明：1．本试卷共有六个大题，23个小题，全卷满分120分，考试时间100分钟。
2．本卷分为试题卷和答题卡，答案要求写在答题卡上，不得在试题卷上作答，否则不给分，
一、选择题（本大题共6小题，每小题3分，共18分．每小题只有一个正确选项）
1．小红每分钟踢键子的次数正常范围为少于80次，但不少于50次，用不等式表示为（ ）
A． B． C． D．
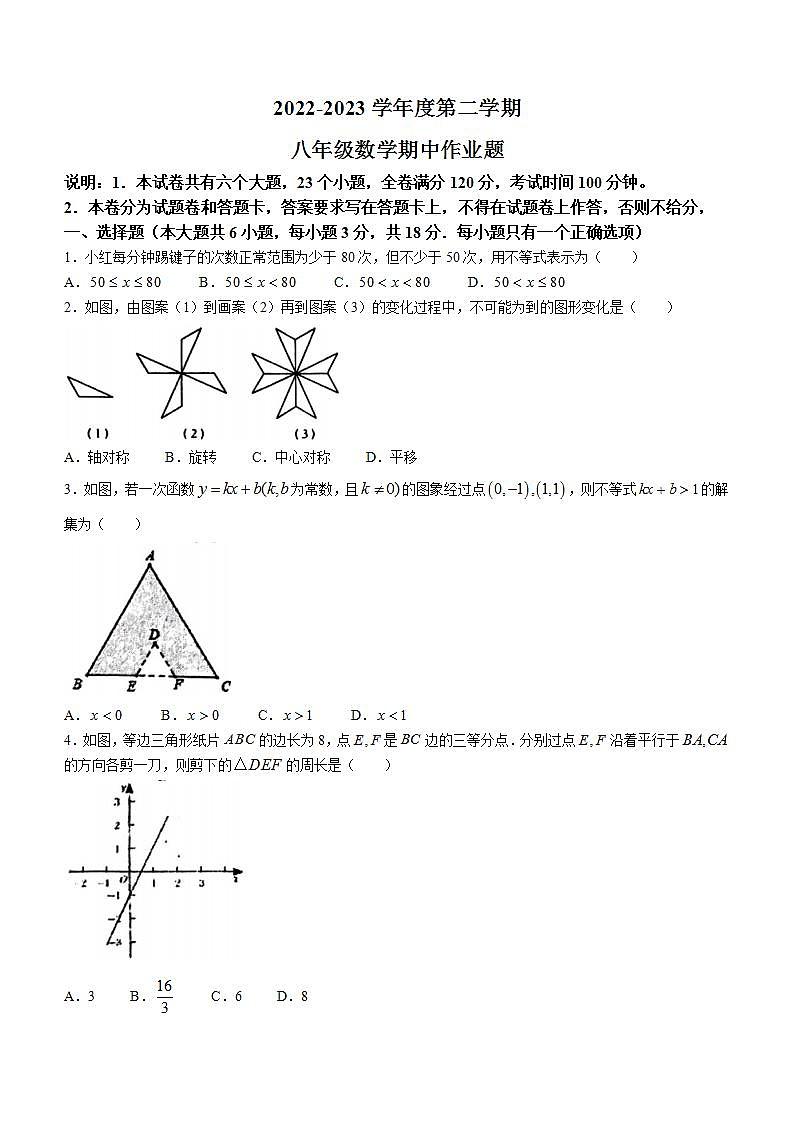
2．如图，由图案（1）到画案（2）再到图案（3）的变化过程中，不可能为到的图形变化是（ ）

A．轴对称 B．旋转 C．中心对称 D．平移
3．如图，若一次函数为常数，且的图象经过点，则不等式的解集为（ ）

A． B． C． D．
4．如图，等边三角形纸片的边长为8，点是边的三等分点．分别过点沿着平行于的方向各剪一刀，则剪下的的周长是（ ）

A．3 B． C．6 D．8
5．若，则下列不等式正确的是（ ）
A． B． C． D．
6．如图，在中，，将绕点逆时针旋转得到，点的对应点分别认，连接．当点在同一条直线上时，下列结论不正确的是（ ）

A． B． C． D．
二、填空题（本大题共6小题，每小题3分，共18分）
7．在平面直角坐标系中，将点向右平移3个单位长度得到点，则点的坐标是_________．
8．如图，x和5分别表示天平上两边的砝码的质量，请你用“>”或“<”填空：_________2．

9．如图，直线经过点，点，直线过点，则不等式的解集为_________．

10．如图，在中，，分别以两点为圆心，大于为半径画弧，两弧交于两点，直线交点，若，则的长度为_________．

11．如图，点按顺时针旋转到，若点恰好在上，则的度数为_________．

12．如图，平分，如果射线上的点满足是等腰三角形，那么的度数为_________．

三、（本大题共5小题，每小题6分，共30分）
13．（本题共2小题，每小题3分）
（1）解不等式：；
（2）如图，，平分交于点，若，求的面积．

14．如图，在中，，斜边的垂直平分线交于点，交于点，求的值．

15．解不等式组：，并把它的解集表示在数轴上．

16．如图，等边的三个顶点都在坐标轴上，，过点作，垂线交轴于点，求点的坐标．

17．如图，一次函数的图象与x轴交于点，一次函数的图象与x轴交于点，且经过点，两函数图象交于点．

（1）求的值和一次函数的解析式；
（2）根据图象，直接写山的解集．
四、（本大题共3小题，每小题8分，共24分）
18．如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，的顶点均在格点上．

（1）画出关于原点的中心对称图形．
（2）将绕点逆时针旋转得到，画出．
（3）若由绕着某点旋转得到的，则这点的坐标为_________．
19．某学校在宣传垃圾分类的实践活动中，需印制主题为“做文明有礼中学生，垃圾分类从我做起”的宣传单，其附近两家图文社印制此种宣传单的收费标准如图所示：

（1）为达到及时宜传的目的，学校同时在A，B两家图文社共印制了800张宣传单，印制费用共计415元，学校在A，B两家图文社各印制了多少张宣传单？
（2）为扩大宣传，学校计划选择B家图文社加印一部分宣传单，在印制费用不超过1450元的前提下，最多可以印制多少张宣传单？
20．如图，在中，，将线段绕点逆时针旋转，得到线段，進接．

（1）依题意补全图形；
（2）若，求线段的长．
五、（本大题2小题，每小题9分，共18分）
21．如图，是的平分线，平移，使点移动到点，点的对应点是，点的对应点是．

（1）在图中画出平移后的；
（2）若，求的度数；
（3）直线与直线相交于点，与直线相交于点，探究，三者之间的数量关系．
22．每年农历五月初五是中国民间的传统节日——端午节。今年端午节，某地甲、乙两家超市为吸引更多的顾客，开展促销活动，对某种质域和售价相同的粽子分别推出了不同的优惠方案，甲超市的方案是：购买该种粽子超过80元后，超出80元的部分按九折收费；乙超市的方案是：购买该种粽子超过120元后，超出120元的部分按八折收费，请根据顾客购买粽子的金额，帮顾客判断到哪家超市购买粽子更划算？
六、（本大题共12分）
23．已知：等边，过点作的平行线．点为线段上一个动点（不与点，重合），将射线绕点顺时针旋转交直线于点．如图1．

（1）依题意补全图形．
（2）求证：；
（3）用等式表示线段之间的数量关系，并证明．
2022-2023学年第二学期八年级数学期中考试参考答案
（仅供参考建议核对）
一、选择题：（每题3分）
1-6 BDCDCA；
二、填空题：（每题3分）
7． 8．< 9． 10． 11． 12．或或
三、13．（1）解：去分母，得，1分
移项，得，
合并同类项，得原不等式的解集为．
（2）过点作，
，
又平分，
，
又，
；
14．解：如图，连接，

是的垂直平分线，
，
，
，
，
．
15．解：解不等式，得：，
解不等式，得：，
则不等式组的解集为．
解集表示在数轴上如图：
16．解：，
是等边三角形，，
，
，
，
，
点的坐标．
17．解：（1）两函数图象交于点，
靶点的坐标代入，得，
解得：，即，
函数经过点，点，
，解得：，即，
所以，一次函数的解析式是；
（2）由图象可知不等式的解集是．
四、18．解：（1）如图，即为所求；
（2）如图，即为所求；

（3）根据旋转的性质可得，旋转中心为和
垂直平分线的交点，图中点即为旋转中心，．
19．解：（1）设学校在图文社印制了张，在图文社印制了张，根据题意得：，
解得：，
答：学校在图文社印制了500张宣传单，在图文社印制了300张宣传单；
（2）设学校最多可印制张宣传单，
由题意得：，
解得：，答：学校最多可印制3000张宣传单．
20．解：（1）如图，即为补全的图形；

（2）在中，，
，
，
，
由旋转可知：，
，
．
五、21、解：（1）如图，三角形即为所求；

（2）平分，
，
；
（3）结论：．
理由：由平移的性质可知，，
，
，
，
．
22．解：设某位顾客要购买x元的该种粽子，
当时，在甲超市的实际花费和在乙超市的实际花费都是x元，
故顾客到甲、乙两家超市购买粽子所花费用相同；
当时，在甲超市超出80元的部分可按九折优惠，而乙超市没有优惠，故顾客到甲超市购买粽子更划算；
当时，在甲超市的实际花费为，
在乙超市的实际花费为，
当时，解得．
当时，解得．
当时，解得．
综上所述，当或时，甲、乙两家超市购买粽子所花费用相同；
当时，顾客到甲超市购买粽子更划算；
当时，顾客到乙超市购买粽子更划算．
六、23．（1）证明：补全图形如图所示，

（2）设交于点，
是等边三角形，
，
将射线绕点顺时针旋转，
，

，
；
（2）解：在上取一点使得，连接，
是等边三角形，

，
，
，
，
．