


所属成套资源:高考数学一轮复习考点测试刷题本(含答案解析)
高考数学一轮复习考点测试刷题本45 两条直线的位置关系与距离公式(含答案解析)
展开这是一份高考数学一轮复习考点测试刷题本45 两条直线的位置关系与距离公式(含答案解析),共7页。
2020高考数学(文数)考点测试刷题本45
两条直线的位置关系与距离公式
1. “直线(m+2)x+3my+1=0与(m-2)x+(m+2)y=0互相垂直”是“m=0.5”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.已知直线x+a2y+6=0与直线(a-2)x+3ay+2a=0平行,则a的值为( )
A.0或3或-1 B.0或3 C.3或-1 D.0或-1
3.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0或2x+y-5=0 B.2x+y+=0或2x+y-=0
C.2x-y+5=0或2x-y-5=0 D.2x-y+=0或2x-y-=0
4.若直线l1:ax+2y-8=0与直线l2:x+(a+1)y+4=0平行,则实数a的值为( )
A.1 B.1或2 C.-2 D.1或-2
5.已知x,y满足x+2y-5=0,则(x-1)2+(y-1)2的最小值为( )
A. B. C. D.
6.若动点A,B分别在直线l1:x+y-7=0和l2:x+y-5=0上移动,则AB的中点M到原点的距离的最小值为( )
A.3 B. C.3 D.2
7.已知点M是直线x+y=2上的一个动点,若点P的坐标为(,-1),则|PM|的最小值为( )
A.0.5 B.1 C.2 D.3
8.已知A(-2,1),B(1,2),点C为直线y=x上的动点,则|AC|+|BC|的最小值为( )
A.2 B.2 C.2 D.2
9. “m=3”是“两直线l1:mx+3y+2=0和l2:x+(m-2)y+m-1=0平行”的________条件.(在“充分不必要”“必要不充分”“充要”“既不充分也不必要”中选一个填空)
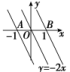
10.设点A(-1,0),B(1,0),直线2x+y-b=0与线段AB相交,则b的取值范围是________.
11.已知点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值为________.
12.在直线3x-4y-27=0上到点P(2,1)距离最近的点的坐标是____________.
13.已知直线l1和l2的方程分别为7x+8y+9=0,7x+8y-3=0,直线l平行于l1,直线l与l1的距离为d1,与l2的距离为d2,且d2=2d1,求直线l的方程.
14.已知△ABC的三个顶点A(4,-6),B(-4,0),C(-1,4),求
(1)AC边上的高BD所在直线方程;
(2)BC边的垂直平分线EF所在直线方程;
(3)AB边的中线的方程.
15.已知椭圆C:![]() ,直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M。
,直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M。
(1)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)若l过点![]() ,延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由。
,延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由。
16.实系数方程f(x)=x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,求:
(1)![]() 的取值范围;
的取值范围;
![]() (2)(a-1)2+(b-2)2的取值范围.
(2)(a-1)2+(b-2)2的取值范围.
(3)a+b-3的值域.
解析:
若直线(m+2)x+3my+1=0与(m-2)x+(m+2)y=0互相垂直,则(m+2)(m-2)+3m(m+2)=0,
解得m=-2或m=,即“直线(m+2)x+3my+1=0与(m-2)x+(m+2)y=0互相垂直”
是“m=”的必要不充分条件.
解析:由题意知1×3a-a2(a-2)=0,即a(a2-2a-3)=0,∴a=0,a=-1或a=3,
经验证当a=3时,两直线重合.故选D.
解析:
设与直线2x+y+1=0平行的直线方程为2x+y+m=0(m≠1),
因为直线2x+y+m=0与圆x2+y2=5相切,即点(0,0)到直线2x+y+m=0的距离为,
所以=,|m|=5.故所求直线的方程为2x+y+5=0或2x+y-5=0.故选A.
解析:
直线l1的方程为y=-x+4.若a=-1,显然两直线不平行,所以a≠-1;
要使两直线平行,则有=,解得a=1或a=-2.
当a=-2时,两直线重合,所以不满足条件,所以a=1.故选A.
解析:
(x-1)2+(y-1)2表示点P(x,y)到点Q(1,1)的距离的平方.
由已知可得点P在直线l:x+2y-5=0上,所以|PQ|的最小值为点Q到直线l的距离,
即d==,所以(x-1)2+(y-1)2的最小值为d2=.故选A.
解析:
点M在直线x+y-6=0上,到原点的最小距离等价于原点O(0,0)到直线x+y-6=0的距离,
即d===3.故选C.
解析:|PM|的最小值即点P(,-1)到直线x+y=2的距离,
又=1,故|PM|的最小值为1.选B.
解析:
设B关于直线y=x的对称点为B′(x0,y0),则解得B′(2,-1).
由平面几何知识得|AC|+|BC|的最小值即是|B′A|==2.故选C.
解析:若l1∥l2,则m(m-2)-3=0,解得m=3或m=-1(此时两直线重合,舍去),所以m=3,
必要性成立;若m=3,k1=k2,l1∥l2,充分性成立,
所以“m=3”是“两直线l1:mx+3y+2=0和l2:x+(m-2)y+m-1=0平行”的充要条件.
解析:b为直线y=-2x+b在y轴上的截距,如图,当直线y=-2x+b过点A(-1,0)和
点B(1,0)时,b分别取得最小值和最大值.所以b的取值范围是[-2,2].
解析:由题意及点到直线的距离公式得=,解得a=-或-.
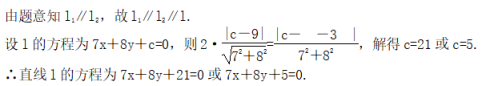

(Ⅰ)设直线![]()
将![]() 代入
代入![]() 得
得![]() ,故
,故
![]()
于是直线![]() 的斜率
的斜率![]() ,即
,即![]()
所以直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值
的斜率的乘积为定值
(Ⅱ)四边形![]() 能为平行四边形
能为平行四边形
因为直线![]() 过点
过点![]() ,所以
,所以![]() 不过原点且与
不过原点且与![]() 有两个交点的充要条件是
有两个交点的充要条件是![]()
由(Ⅰ)得![]() 的方程为
的方程为![]()
设点![]() 的横坐标为
的横坐标为![]()
由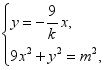 得
得![]() ,即
,即![]()
将点![]() 的坐标代入
的坐标代入![]() 的方程得
的方程得![]() ,因此
,因此![]()
四变现![]() 为平行四边形当且仅当线段
为平行四边形当且仅当线段![]() 与线段
与线段![]() 互相平分,即
互相平分,即![]()
于是![]() ,解得
,解得![]()
因为![]() ,所以当
,所以当![]() 的斜率为
的斜率为![]() 或
或![]() 时,四边形
时,四边形![]() 为平行四边形
为平行四边形

相关试卷
这是一份高考数学一轮复习考点测试刷题本47 椭圆(含答案解析),共8页。
这是一份高考数学一轮复习考点测试刷题本39 复数(含答案解析),共5页。
这是一份高考数学一轮复习考点测试刷题本32 等比数列前n项和公式(含答案解析),共6页。













