高考数学一轮复习考点测试刷题本44 直线的方程（含答案解析）

2020高考数学(文数)考点测试刷题本44

直线的方程

一         、选择题

1.在下列四个命题中，正确的有(　　)

①坐标平面内的任何一条直线均有倾斜角与斜率；

②直线的倾斜角的取值范围为[0°，180°]；

③若一直线的斜率为tanα，则此直线的倾斜角为α；

④若一直线的倾斜角为α，则此直线的斜率为tanα．

A．0个          B．1个         C．2个            D．3个

2.若过点P(1-a,1＋a)和Q(3,2a)的直线的倾斜角为钝角，则实数a的取值范围是(　　)

A．(-2,1)       B．(-1,2)      C．(-∞，0)      D．(-∞，-2)∪(1，＋∞)

3.若θ是直线l的倾斜角，且sinθ＋cosθ=，则l的斜率为(　　)

A．-0.5      B．-0.5或-2       C．0.5或2     D．-2

4.直线2x-my＋1-3m=0，当m变动时，所有直线都通过定点(　　)

A．       B．      C．      D．

5.直线，直线，若，则实数（   ）

A.-1         B.2     C.-1或2        D.不存在

6.已知直线l1：(k-3)x＋(5-k)y＋1=0与l2：2(k-3)x-2y＋3=0垂直，则k的值为(　　)

A．1或3        B．1或5         C．1或4           D．1或2

7.已知直线y=2x是△ABC中∠C的平分线所在的直线，若点A，B的坐标分别是(－4，2)，(3，1)，则点C的坐标为(　　)

A．(－2，4)          B．(－2，－4)        C．(2，4)            D．(2，－4)

8.在△ABC中，A(1，1)，B(m，)(1＜m＜4)，C(4，2)，则当△ABC面积最大时，m=(　　)

A.           B．           C.            D．

二         、填空题

9.若过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角，则实数a的取值范围是      .

10.直线l：xcos α＋y＋2=0的倾斜角的取值范围是________________．

11.不论m取何值，直线(m－1)x－y＋2m＋1=0恒过定点________.

12.已知直线y=x＋k与两坐标轴围成的三角形的面积不小于1，则实数k的取值范围是________．

三         、解答题

13.已知△ABC的顶点B(﹣1，﹣3)，边AB上的高CE所在直线的方程为4x+3y﹣7=0，BC边上中线AD所在的直线方程为x﹣3y﹣3=0.

(1)求点C的坐标；

(2)求直线AB的方程.             

14.已知点P(2，－1)．

(1)求过点P且与原点的距离为2的直线l的方程；

(2)求过点P且与原点的距离最大的直线l的方程，最大距离是多少？

15.设直线l的方程为(a＋1)x＋y-2-a=0(a∈R)．

(1)若直线l在两坐标轴上的截距相等，求直线l的方程；

(2)若a>-1，直线l与x，y轴分别交于M，N两点，O为坐标原点，求△OMN面积取最小值时直线l的方程．

16.直线l过点P(1,4),分别交x轴的正半轴和y轴的正半轴于A,B两点.

(1)当|PA|·|PB|最小时,求l的方程;

(2)当|OA|+|OB|最小时,求l的方程.

答案解析

1.答案为：A；

解析：

当倾斜角α=90°时，其斜率不存在，故①④不正确；直线的倾斜角α的取值范围为[0°，180°)，故②不正确；直线的斜率k=tan210°这是可以的，此时倾斜角α=30°而不是210°，故③不正确．故选A．

2.答案为：A；

解析：

∵过点P(1-a,1＋a)和Q(3,2a)的直线的倾斜角为钝角，∴直线的斜率小于0，

即<0，即<0，解得-2<a<1，故选A．

3.答案为：D；

4.答案为：D；

5.A

6.

7.答案为：C.

解析：设A(－4，2)关于直线y=2x的对称点为(x，y)，则解得

所以BC所在直线方程为y－1=(x－3)，即3x＋y－10=0.

同理可得点B(3，1)关于直线y=2x的对称点为(－1，3)，

所以AC所在直线方程为y－2=·(x＋4)，

即x－3y＋10=0.联立得解得则C(2，4)．故选C.

8.答案为：B.

解析：由两点间距离公式可得|AC|=，直线AC的方程为x－3y＋2=0，

所以点B到直线AC的距离d=，

从而△ABC的面积S=|AC|d=|m－3＋2|=

又1＜m＜4，所以1＜＜2，所以当=，即m=时，S取得最大值．

9.答案为：-2<a<1.

10.答案为：∪；

解析：设直线l的倾斜角为θ，依题意知，θ≠，直线l的斜率k=－cos α，

∵cos α∈[－1,1]，∴k∈，即tan θ∈.

又θ∈[0，π)，∴θ∈∪.

11.答案为：(-2,3)

12.答案为：(-∞，-1]∪[1，＋∞)；

解析：

令y=0，则x=-2k．令x=0，则y=k．

故直线与两坐标轴围成的三角形的面积为S=|k|·|-2k|=k2．

由题意知，三角形的面积不小于1，可得k2≥1，

所以实数k的取值范围是k≥1或k≤-1．

13.解：                                         

14.解：

(1)过点P的直线l与原点的距离为2，而点P的坐标为(2，－1)，

显然，过P(2，－1)且垂直于x轴的直线满足条件，

此时l的斜率不存在，其方程为x=2.

若斜率存在，设l的方程为y＋1=k(x－2)，

即kx－y－2k－1=0.

由已知得=2，解得k=.

此时l的方程为3x－4y－10=0.

综上，可得直线l的方程为x=2或3x－4y－10=0.

(2)作图可得过点P与原点O的距离最大的直线是过点P且与PO垂直的直线，如图．

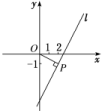
由l⊥OP，得klkOP=－1，所以kl=－=2.

由直线方程的点斜式得y＋1=2(x－2)，即2x－y－5=0.

所以直线2x－y－5=0是过点P且与原点O的距离最大的直线，

最大距离为=.

15.解：

(1)当直线l经过坐标原点时，该直线在两坐标轴上的截距都为0，

此时a＋2=0，解得a=-2，此时直线l的方程为-x＋y=0，即x-y=0；

当直线l不经过坐标原点，即a≠-2且a≠-1时，

由直线在两坐标轴上的截距相等可得=2＋a，解得a=0，

此时直线l的方程为x＋y-2=0．

所以直线l的方程为x-y=0或x＋y-2=0．

(2)由直线方程可得M，N(0,2＋a)，

因为a>-1，所以S△OMN=··(2＋a)

=×=≥×=2，

当且仅当a＋1=，即a=0时等号成立．

此时直线l的方程为x＋y-2=0．

16.