


所属成套资源:高考数学一轮复习考点测试刷题本(含答案解析)
高考数学一轮复习考点测试刷题本32 等比数列前n项和公式(含答案解析)
展开
这是一份高考数学一轮复习考点测试刷题本32 等比数列前n项和公式(含答案解析),共6页。
2020高考数学(文数)考点测试刷题本32 等比数列前n项和公式 一 、选择题1.已知等比数列{an}的前n项和为Sn=a·2n-1+,则a的值为( )A.- B. C.- D. 2.设首项为1,公比为的等比数列{an}的前n项和为Sn,则( )A.Sn=2an-1 B.Sn=3an-2 C.Sn=4-3an D.Sn=3-2an 3.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上题的已知条件,若要使织布的总尺数不少于30,该女子所需的天数至少为( )A.7 B.8 C.9 D.10 4.等差数列{an}的公差是2,若a2,a4,a8成等比数列,则{an}的前n项和Sn=( )A.n(n+1) B.n(n-1) C. D. 5.已知等比数列{an}的前n项和Sn=a·3n-1+b,则=( )A.-3 B.-1 C.1 D.3 6.设Sn是等比数列{an}的前n项和,若=3,则=( )A.2 B. C. D.1或2 7.设首项为1,公比为的等比数列{an}的前n项和为Sn,则下列结论正确的是( )A.Sn=4-3an B.Sn=3-2an C.Sn=3an-2 D.Sn=2an-1 8.已知等比数列{an}的前n项积为Tn,若a1=-24,a4=-,则当Tn取得最大值时,n的值为( )A.2 B.3 C.4 D.6 二 、填空题9.设公比为q的等比数列{an}的前n项和为Sn,若S2=3a2+2,S4=3a4+2,则q=________. 10.设公比为q(q>0)的等比数列{an}的前n项和为Sn,若S2=3a2+2,S4=3a4+2,则q=________. 11.在数列{an}中,已知a1=1,an=2(an-1+an-2+…+a2+a1)(n≥2,n∈N*),则这个数列的前4项和S4=________. 12.已知等差数列{an}的公差为d,等比数列{bn}的公比为q,设{an},{bn}的前n项和分别为Sn,Tn,若n2(Tn+1)=2nSn,n∈N*,则d=________,q=________. 三 、解答题13.等比数列{an}中,a1=1,a5=4a3.(1)求{an}的通项公式;(2)记Sn为{an}的前n项和.若Sm=63,求m. 14.在数列{an}中,a+2an+1=anan+2+an+an+2,且a1=2,a2=5.(1)证明:数列{an+1}是等比数列;(2)求数列{an}的前n项和Sn. 15.设数列{an}的各项均为正数,且a2=4a1,an+1=a+2an(n∈N*).(1)证明:数列{log3(1+an)}为等比数列;(2)设数列{log3(an+1)}的前n项和为Tn,求使Tn>520成立时n的最小值. 16.已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列.(1)求数列{an}的通项公式;(2)设Tn为数列前n项的和,若λTn≤an+1对一切n∈N*恒成立,求实数λ的最大值.
答案解析1.答案为:A. 2.答案为:D;由等比数列前n项和公式Sn=,代入数据可得Sn=3-2an. 3.答案为:B.解析:设该女子第一天织布x尺,则=5,得x=,∴前n天所织布的尺数为(2n-1).由(2n-1)≥30,得2n≥187,则n的最小值为8. 4.答案为:A; 5.答案为:A;解析:∵等比数列{an}的前n项和Sn=a·3n-1+b,∴a1=S1=a+b,a2=S2-S1=3a+b-a-b=2a,a3=S3-S2=9a+b-3a-b=6a,∵等比数列{an}中,a=a1a3,∴(2a)2=(a+b)×6a,解得=-3.故选A. 6.答案为:B;解析:设S2=k,则S4=3k,由数列{an}为等比数列(易知数列{an}的公比q≠-1),得S2,S4-S2,S6-S4为等比数列,又S2=k,S4-S2=2k,∴S6-S4=4k,∴S6=7k,∴==,故选B. 7.答案为:B;解析:由题意,an=n-1,Sn==31-n=3-2×n-1,所以Sn=3-2an,故选B. 8.答案为:C;设等比数列{an}的公比为q,则a4=-24q3=-,所以q3=,q=,易知此等比数列各项均为负数,则当n为奇数时,Tn为负数,当n为偶数时,Tn为正数,所以Tn取得最大值时,n为偶数,排除B,而T2=(-24)2×=24×8=192,T4=(-24)4×6=84×=>192,T6=(-24)6×15=86×9==×<,所以T4最大.故选C. 9.答案为:1.5或-1;解析:∵公比为q的等比数列{an}的前n项和为Sn,且S2=3a2+2,S4=3a4+2,∴S4-S2=a4+a3=3a4-3a2,即2q2-q-3=0,∴q=1.5或-1.10.答案为:1.5; 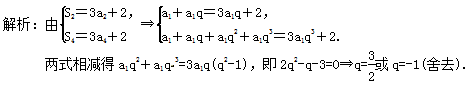 11.答案为:27;解析:由已知n≥2时,an=2Sn-1,an+1=2Sn,∴an+1-an=2an,即an+1=3an(n≥2),∴an=∴S4=1+2+6+18=27. 12.答案为:2,2;解析:由题意得,=⇒=,∴q=2,=1,a1=,=1,此时d=2,q=2. 13.解:(1)设{an}的公比为q,由题设得an=qn-1.由已知得q4=4q2,解得q=0(舍去),q=-2或q=2.故an=(-2)n-1或an=2n-1.(2)若an=(-2)n-1,则Sn=.由Sm=63得(-2)m=-188,此方程没有正整数解.若an=2n-1,则Sn=2n-1.由Sm=63得2m=64,解得m=6.综上,m=6. 14.解:(1)证明:∵a+2an+1=anan+2+an+an+2,∴(an+1+1)2=(an+1)(an+2+1),即=.∵a1=2,a2=5,∴a1+1=3,a2+1=6,∴=2,∴数列{an+1}是以3为首项,2为公比的等比数列.(2)由(1)知,an+1=3·2n-1,∴an=3·2n-1-1,∴Sn=-n=3·2n-n-3. 15.解:(1)证明:由已知,得a2=a+2a1=4a1,则a1(a1-2)=0,因为数列{an}的各项均为正数,所以a1=2.因为an+1+1=(an+1)2>0,所以log3(an+1+1)=2log3(an+1).又log3(a1+1)=log33=1,所以数列{log3(1+an)}是首项为1,公比为2的等比数列.(2)由(1)可知,log3(1+an)=2n-1,所以Tn=1+2+22+…+2n-1=2n-1.由Tn>520,得2n>521(n∈N*),得n≥10.则使Tn>520成立时n的最小值为10. 16.解:(1)设公差为d,由已知得解得d=1或d=0(舍去),所以a1=2,所以an=n+1.(2)因为=-,所以Tn=++…+-=-=,又λTn≤an+1对一切n∈N*恒成立,所以λ≤=2+8,而2+8≥16,当且仅当n=2时等号成立.所以λ≤16,即λ的最大值为16.
11.答案为:27;解析:由已知n≥2时,an=2Sn-1,an+1=2Sn,∴an+1-an=2an,即an+1=3an(n≥2),∴an=∴S4=1+2+6+18=27. 12.答案为:2,2;解析:由题意得,=⇒=,∴q=2,=1,a1=,=1,此时d=2,q=2. 13.解:(1)设{an}的公比为q,由题设得an=qn-1.由已知得q4=4q2,解得q=0(舍去),q=-2或q=2.故an=(-2)n-1或an=2n-1.(2)若an=(-2)n-1,则Sn=.由Sm=63得(-2)m=-188,此方程没有正整数解.若an=2n-1,则Sn=2n-1.由Sm=63得2m=64,解得m=6.综上,m=6. 14.解:(1)证明:∵a+2an+1=anan+2+an+an+2,∴(an+1+1)2=(an+1)(an+2+1),即=.∵a1=2,a2=5,∴a1+1=3,a2+1=6,∴=2,∴数列{an+1}是以3为首项,2为公比的等比数列.(2)由(1)知,an+1=3·2n-1,∴an=3·2n-1-1,∴Sn=-n=3·2n-n-3. 15.解:(1)证明:由已知,得a2=a+2a1=4a1,则a1(a1-2)=0,因为数列{an}的各项均为正数,所以a1=2.因为an+1+1=(an+1)2>0,所以log3(an+1+1)=2log3(an+1).又log3(a1+1)=log33=1,所以数列{log3(1+an)}是首项为1,公比为2的等比数列.(2)由(1)可知,log3(1+an)=2n-1,所以Tn=1+2+22+…+2n-1=2n-1.由Tn>520,得2n>521(n∈N*),得n≥10.则使Tn>520成立时n的最小值为10. 16.解:(1)设公差为d,由已知得解得d=1或d=0(舍去),所以a1=2,所以an=n+1.(2)因为=-,所以Tn=++…+-=-=,又λTn≤an+1对一切n∈N*恒成立,所以λ≤=2+8,而2+8≥16,当且仅当n=2时等号成立.所以λ≤16,即λ的最大值为16.
相关试卷
这是一份高考数学一轮复习考点测试刷题本31 等比数列及通项公式(含答案解析),共6页。
这是一份高考数学一轮复习考点测试刷题本30 等差数列前n项和公式(含答案解析),共6页。
这是一份高考数学一轮复习考点测试刷题本29 等差数列及通项公式(含答案解析),共5页。











