高考数学一轮复习考点测试刷题本42 直线平面平行的判定及其性质（含答案解析）

2020高考数学(文数)考点测试刷题本42

直线平面平行的判定及其性质

一         、选择题

1.已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是(　　)

A．若α⊥γ，α⊥β，则γ∥β

B．若m∥n，m⊂α，n⊂β，则α∥β

C．若m∥n，m⊥α，n⊥β，则α∥β

D．若m∥n，m∥α，则n∥α

2.两条直线a，b满足a∥b，b⊂α，则a与平面α的位置关系是(　　)

A．a∥α        B．a⊂α      C．a与α相交      D．a与α不相交

3.如图所示的三棱柱ABC－A1B1C1中，过A1B1的平面与平面ABC交于DE，则DE与AB的位置关系是(　　)

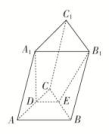
A．异面         B．平行         C．相交         D．以上均有可能

4.下列命题中，错误的是(　　)

A．平面内一个三角形各边所在的直线都与另一个平面平行，则这两个平面平行

B．平行于同一个平面的两个平面平行

C．若两个平面平行，则位于这两个平面内的直线也互相平行

D．若两个平面平行，则其中一个平面内的直线平行于另一个平面

5.若直线l不平行于平面α，且l⊄α，则(　　)

A．α内的所有直线与l异面

B．α内不存在与l平行的直线

C．α内存在唯一的直线与l平行

D．α内的直线与l都相交

6.有下列命题：

①若直线l平行于平面α内的无数条直线，则直线l∥α；

②若直线a在平面α外，则a∥α；

③若直线a∥b，b∥α，则a∥α；

④若直线a∥b，b∥α，则a平行于平面α内的无数条直线．

其中真命题的个数是(　　)

A．1         B．2           C．3             D．4

7.已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的(　　)

A．充分不必要条件          B．必要不充分条件

C．充分必要条件            D．既不充分也不必要条件

8.在三棱锥A－BCD中，E，F，G，H分别是AB，BC，CD，DA上的点，当BD∥平面EFGH时，下面结论正确的是(　　)

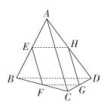
A．E，F，G，H一定是各边的中点

B．G，H一定是CD，DA的中点

C．BE∶EA=BF∶FC，且DH∶HA=DG∶GC

D．AE∶EB=AH∶HD且BF∶FC=DG∶GC

二         、填空题

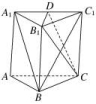
9.如图所示，三棱柱ABC ­A1B1C1的侧面BCC1B1是菱形，设D是A1C1上的点且A1B∥平面B1CD，则A1D∶DC1的值为________．

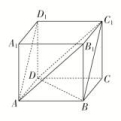
10.已知正方体ABCD­A1B1C1D1，下列结论中，正确的是________(只填序号)．

①AD1∥BC1；②平面AB1D1∥平面BDC1；③AD1∥DC1；④AD1∥平面BDC1.

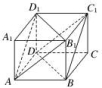
11.已知正方体ABCD－A1B1C1D1，下列结论中，正确的结论是________(只填序号)．

①AD1∥BC1；②平面AB1D1∥平面BDC1；③AD1∥DC1；④AD1∥平面BDC1．

12.α，β是两个平面，m，n是两条直线，有下列四个命题：

①如果m⊥n，m⊥α，n∥β，那么α⊥β；

②如果m⊥α，n∥α，那么m⊥n；

③如果α∥β，m⊂α，那么m∥β；

④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．

其中正确的命题有________．(填写所有正确命题的编号)

三         、解答题

13.在平行六面体ABCD－A1B1C1D1中，AA1=AB，AB1⊥B1C1．求证：

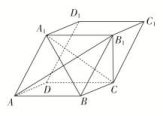
(1)AB∥平面A1B1C；

(2)平面ABB1A1⊥平面A1BC．

14.如图，△ABC中，AC=BC=AB，四边形ABED是边长为1的正方形，平面ABED⊥底面ABC，G，F分别是EC，BD的中点．

(1)求证：GF∥底面ABC；

(2)求几何体ADEBC的体积．

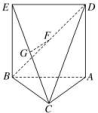
15.如图，四棱锥P－ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．

(1)证明：MN∥平面PAB；

(2)求四面体N－BCM的体积．

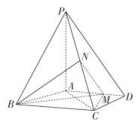
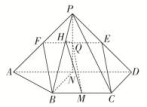
16.如图，已知四棱锥P－ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．

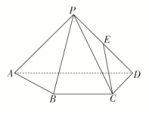
(1)证明：CE∥平面PAB；

(2)求直线CE与平面PBC所成角的正弦值．

答案解析

1.答案为：C；

解析：对于A，若α⊥γ，α⊥β，则γ∥β或γ与β相交；对于B，若m∥n，m⊂α，n⊂β，

则α∥β或α与β相交；易知C正确；对于D，若m∥n，m∥α，则n∥α或n在平面α内．

故选C.

2.答案为：D；

解析：由于b⊂α且a∥b，则a∥α或a⊂α．故a与α不相交．故选D．

3.答案为：B；

解析：

在三棱柱ABC－A1B1C1中，AB∥A1B1，∵AB⊂平面ABC，A1B1⊄平面ABC，∴A1B1∥平面ABC，

∵过A1B1的平面与平面ABC交于DE．∴DE∥A1B1，∴DE∥AB．

4.答案为：C；

解析：

由面面平行的判定定理和性质知A，B，D正确．对于C，位于两个平行平面内的直线也可能异面．

5.答案为：B；

解析：因为l⊄α，若在平面α内存在与直线l平行的直线，则l∥α，这与题意矛盾．故选B．

6.答案为：A；

解析：

命题①，l可以在平面α内，是假命题；

命题②，直线a与平面α可以是相交关系，是假命题；

命题③，a可以在平面α内，是假命题；

命题④是真命题．

7.答案为：A；

解析：

∵m⊄α，n⊂α，m∥n，∴m∥α，故充分性成立．而由m∥α，n⊂α，得m∥n或m与n异面，

故必要性不成立．故选A．

8.答案为：D；

解析：由BD∥平面EFGH，得BD∥EH，BD∥FG，则AE∶EB=AH∶HD，且BF∶FC=DG∶GC．故选D．

一         、填空题

9.答案为：1；

解析：设BC1∩B1C=O，连接OD.∵A1B∥平面B1CD且平面A1BC1∩平面B1CD=OD，∴A1B∥OD，

∵四边形BCC1B1是菱形，∴O为BC1的中点，∴D为A1C1的中点，则A1D∶DC1=1.

10.答案为：①②④；

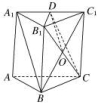
解析：连接AD1，BC1，AB1，B1D1，C1D，BD，因为AB綊C1D1，所以四边形AD1C1B为平行四边形，

故AD1∥BC1，从而①正确；易证BD∥B1D1，AB1∥DC1，又AB1∩B1D1=B1，BD∩DC1=D，

故平面AB1D1∥平面BDC1，从而②正确；由图易知AD1与DC1异面，故③错误；

因为AD1∥BC1，AD1⊄平面BDC1，BC1⊂平面BDC1，故AD1∥平面BDC1，故④正确．

11.答案为：①②④；

解析：

连接AD1，BC1，AB1，B1D1，C1D，BD，则AD1∥BC1，从而①正确；易证BD∥B1D1，AB1∥DC1，

又AB1∩B1D1=B1，BD∩DC1=D，故平面AB1D1∥平面BDC1，从而②正确；

由图易知AD1与DC1异面，故③错误；

因AD1∥BC1，AD1⊄平面BDC1，BC1⊂平面BDC1，故AD1∥平面BDC1，故④正确．

12.答案为：②③④；

解析：

由m⊥n，m⊥α，可得n∥α或n在α内，当n∥β时，α与β可能相交，也可能平行，故①错．

易知②③④都正确．

二         、解答题

13.证明：

(1)在平行六面体ABCD－A1B1C1D1中，AB∥A1B1，

因为AB⊄平面A1B1C，A1B1⊂平面A1B1C，

所以AB∥平面A1B1C．

(2)在平行六面体ABCD－A1B1C1D1中，四边形ABB1A1为平行四边形．

又因为AA1=AB，所以四边形ABB1A1为菱形，所以AB1⊥A1B．

因为AB1⊥B1C1，BC∥B1C1，所以AB1⊥BC．

又因为A1B∩BC=B，A1B⊂平面A1BC，BC⊂平面A1BC，所以AB1⊥平面A1BC，

又因为AB1⊂平面ABB1A1，

所以平面ABB1A1⊥平面A1BC．

14.解：

(1)证明：如图，取BC的中点M，AB的中点N，连接GM，FN，MN.

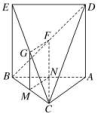
∵G，F分别是EC，BD的中点，

∴GM∥BE，且GM=BE，

NF∥DA，且NF=DA.

又四边形ABED为正方形，∴BE∥AD，BE=AD，

∴GM∥NF且GM=NF.

∴四边形MNFG为平行四边形．

∴GF∥MN，又MN⊂平面ABC，GF⊄平面ABC，

∴GF∥平面ABC.

(2)连接CN，∵AC=BC，∴CN⊥AB，

又平面ABED⊥平面ABC，CN⊂平面ABC，

∴CN⊥平面ABED.

易知△ABC是等腰直角三角形，∴CN=AB=，

∵C­ABED是四棱锥，

∴VC­ABED=S四边形ABED·CN=×1×=.

15.解：

(1)证明：由已知得AM=AD=2，

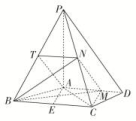
取BP的中点T，连接AT，TN，由N为PC中点知TN∥BC，TN=BC=2．

又AD∥BC，故TN綊AM，故四边形AMNT为平行四边形，于是MN∥AT．

因为AT⊂平面PAB，MN⊄平面PAB，

所以MN∥平面PAB．

(2)因为PA⊥平面ABCD，N为PC的中点，

所以N到平面ABCD的距离为PA．

取BC的中点E，连接AE．

由AB=AC=3得AE⊥BC，AE==．

由AM∥BC得M到BC的距离为，

故S△BCM=×4×=2．

所以四面体N－BCM的体积VN－BCM=·S△BCM·=×2×2=．

16.解：

(1)证明：如图，设PA的中点为F，连接EF，FB．

因为E，F分别为PD，PA的中点，所以EF∥AD且EF=AD．

又因为BC∥AD，BC=AD，

所以EF∥BC且EF=BC，

所以四边形BCEF为平行四边形，所以CE∥BF．

因为BF⊂平面PAB，CE⊄平面PAB，

所以CE∥平面PAB．

(2)分别取BC，AD的中点M，N．

连接PN交EF于点Q，连接MQ．

因为E，F，N分别是PD，PA，AD的中点，

所以Q为EF的中点．

在平行四边形BCEF中，MQ∥CE．

由△PAD为等腰直角三角形得PN⊥AD．

由DC⊥AD，BC∥AD，BC=AD，N是AD的中点得BN⊥AD．所以AD⊥平面PBN．

由BC∥AD得BC⊥平面PBN，

那么平面PBC⊥平面PBN．

过点Q作PB的垂线，

垂足为H，连接MH，

MH是MQ在平面PBC上的射影，

所以∠QMH是直线CE与平面PBC所成的角．

设CD=1．

在△PCD中，由PC=2，CD=1，PD=得CE=，

在△PBN中，由PN=BN=1，PB=得QH=，

在Rt△MQH中，QH=，MQ=，

所以sin∠QMH=．

所以，直线CE与平面PBC所成角的正弦值是．