所属成套资源：高考数学一轮复习作业本 （含答案）
高考数学一轮复习作业本7.3 直线、平面的垂直关系（含答案）
展开这是一份高考数学一轮复习作业本7.3 直线、平面的垂直关系（含答案），共7页。
2020高考数学(理数)复习作业本7.3
直线、平面的垂直关系
1.已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则( )
A．m∥l B．m∥n C．n⊥l D．m⊥n
2.如图所示，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过点C1作C1H⊥底面ABC，
垂足为H，则点H在( )
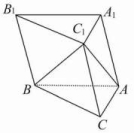
A.直线AC上 B.直线AB上 C.直线BC上 D.△ABC的内部
3.下列命题中：①平行于同一直线的两个平面平行；②平行于同一个平面的两个平面平行；③垂直于同一直线的两直线平行；④垂直于同一平面的两直线平行，其中正确的个数有( )
A.1 B.2 C.3 D.4
A.若直线a∥平面α，直线b⊥a，b
平面β，则α⊥β
B.若直线a⊥直线b，a⊥平面α，b⊥平面β，则α⊥β
C.过平面外的一条直线有
且只有一个平面与已知平面垂直
D.过平面外一点有且只有一个平面与已知平面垂直
b一定不垂直于α；b可能垂直于平面α；b一定不平行于平面α.
其中正确的结论有
A、0个 B、1个 C、2个 D、3个
6.如图，在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，下面四个结论中不成立的是( )
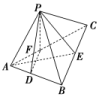
A.BC∥平面PDF B.DF⊥平面PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
7.已知l，m，n为两两垂直的三条异面直线，过l作平面α与直线m垂直，则直线n与平面α的关系是( ).
A.n∥α B.n∥α或n⊂α C.n⊂α或n与α不平行 D.n⊂α
①如果直线l与平面α内的无数条直线垂直，则l⊥α；
②如果直线l不垂直于α，则α内没有与l垂直的直线；
③如果一条直线与平面内的一条直线垂直，则该直线与此平面必相交；
④如果一条直线和平面的一条垂线垂直，该直线必在这个平面内；
⑤如果一条直线和一个平面垂直，该直线垂直于平面内的任一直线.
A.0 B.1 C.2 D.3
9.过平面外一点作该平面的垂线有 条；垂面有 个；平行线有 条；平行平面有 个.
10.如图,在三棱锥D-ABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有 (写出全部正确命题的序号).
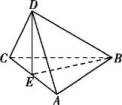
①平面ABC⊥平面ABD;
②平面ABD⊥平面BCD;
③平面ABC⊥平面BDE,且平面ACD⊥平面BDE;
④平面ABC⊥平面ACD,且平面ACD⊥平面BDE.
11.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,且E为CD的中点,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,连接DC,则下列说法正确的是 .(写出所有正确说法的序号)
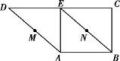
①无论D折至何位置(不在平面ABC内),都有MN∥平面DEC;
②无论D折至何位置(不在平面ABC内),都有MN⊥AE;
③无论D折至何位置(不在平面ABC内),都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
12.边长为a的正三角形ABC的边AB、AC的中点为E、F，将△AEF沿EF折起，此时A点的新位置A′使平面A′EF⊥平面BEFC，则A′B=________.
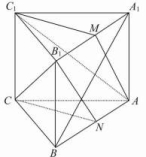
14.如图，在几何体ABCA1B1C1中，点A1，B1，C1在平面ABC内的正投影分别为A，B，C，且AB⊥BC，E为AB1的中点，AB=AA1=BB1=2CC1.
(1)求证：CE∥平面A1B1C1；
(2)求证：平面AB1C1⊥平面A1BC.
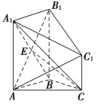
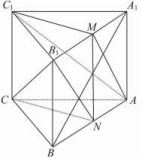
15.三棱柱ABC-A1B1C1中，侧棱A1A垂直于底面ABC，B1C1=A1C1，AC1⊥A1B，M，N分别为A1B1，AB的中点.
求证：（1）平面AMC1∥平面NB1C；（2）A1B⊥AM.
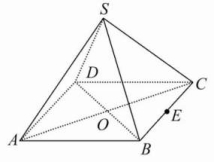
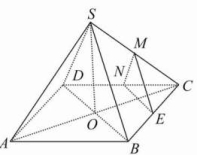
16.如图，在四棱锥S-ABCD中，侧棱SA=SB=SC=SD，底面ABCD是菱形，AC与BD交于O点.
（1）求证：AC⊥平面SBD；
（2）若E为BC的中点，点P在侧面△SCD内及其边界上运动，并保持PE⊥AC，试指出动点P的轨迹，并证明你的结论.
解析：因为α∩β=l，所以l⊂β，又n⊥β，所以n⊥l.故选C.
2.【解析】选B.∵BC1⊥AC，BA⊥AC，BC1∩BA=B,
∴AC⊥平面BC1A，又AC
平面BAC,∴平面BAC⊥平面BC1A.
∵C1H⊥平面ABC，且点H为垂足，平面BAC∩平面BC1A=AB,∴H∈AB.
【解析】①中两个平面可能平行可能相交；②正确；③两直线可能平行、垂直也可能异面；④正确.
6.【答案】 C【解析】 由题意知BC∥DF，且BC⊥PE，BC⊥AE.∵PE∩AE=E，∴BC⊥平面PAE，
∴BC∥平面PDF成立，DF⊥平面PAE成立，平面PAE⊥平面ABC也成立.
7.答案:A;解析:∵l⊂α，且l与n异面，∴n⊄α，又∵m⊥α，n⊥m，∴n∥α
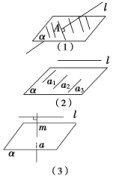
8.【答案】 B【解析】 如图(1)所示，l与α相交(不垂直)，此时也有无数条直线与l垂直.故①②错误；如图(2)所示，l与α平行，此时平面内也存在无数条直线与l垂直，故③④错误；如图(3)所示，直线l与平面α的垂线m垂直，但l不在平面α内；由线面垂直的定义可知，⑤正确.
10.答案：③；解析 因为AB=CB,且E是AC的中点,所以BE⊥AC,同理,DE⊥AC,由于DE∩BE=E,于是AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又AC⊂平面ACD,所以平面ACD⊥平面BDE.
11.
答案 ①②④解析 由已知得,在未折叠的原梯形中,AB?DE,
所以四边形ABED为平行四边形,所以BE=AD.折叠后的图形如图所示.
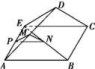
①过点M作MP∥DE,交AE于点P,连接NP.
因为M是AD的中点,所以点P为AE的中点,又N为BE的中点,故NP∥EC.
又MP∩NP=P,DE∩CE=E,所以平面MNP∥平面DEC,故MN∥平面DEC,①正确.
②由已知可得AE⊥ED,AE⊥EC,所以AE⊥MP,AE⊥NP,
又MP∩NP=P,所以AE⊥平面MNP,又MN⊂平面MNP,所以MN⊥AE,②正确.
③假设MN∥AB,则MN与AB确定平面MNBA,
从而BE⊂平面MNBA,AD⊂平面MNBA,与BE和AD是异面直线矛盾,③错误.
④当EC⊥ED时,EC⊥AD.因为EC⊥EA,EC⊥ED,EA∩ED=E,所以EC⊥平面AED,又AD⊂平面AED,
所以EC⊥AD,④正确.
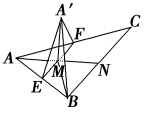
12.【答案】a;【解析】:取BC的中点N，连接AN交EF于点M，连接A′M，则A′M⊥EF.
∵平面A′EF⊥平面BCFE，∴A′M⊥平面BCFE，∴A′M⊥BM，
∵AM=MN=AN=a，∴A′M=a，在Rt△MNB中，MB2=MN2＋NB2=a2，
在Rt△A′MB中，A′B==a.
∵
，
∴
，
∴
平面
，
又∵
平面，
∴
(1)由题意知AA1⊥平面ABC，BB1⊥平面ABC，CC1⊥平面ABC，
∴AA1∥BB1∥CC1.
如图，取A1B1的中点F，连接EF，FC1.
∵E为AB1的中点，∴EF綊A1A，
又AA1=2CC1，∴CC1綊AA1，∴EF綊CC1，
∴四边形EFC1C为平行四边形，
∴CE∥C1F.
又CE⊄平面A1B1C1，C1F⊂平面A1B1C1，
∴CE∥平面A1B1C1.
(2)∵BB1⊥平面ABC，∴BB1⊥BC.
又AB⊥BC，AB∩BB1=B，∴BC⊥平面AA1B1B.
∵AB1⊂平面AA1B1B，∴BC⊥AB1.
∵AA1=BB1=AB，AA1∥BB1，
∴四边形AA1B1B为正方形，∴AB1⊥A1B.
∵A1B∩BC=B，
∴AB1⊥平面A1BC.
∵AB1⊂平面AB1C1，
∴平面AB1C1⊥平面A1BC.
15.解：（1）∵M，N分别为A1B1，AB的中点，∴B1M 
NA，∴B1N∥AM.
又AM平面AMC1，B1N
平面AMC1，∴B1N∥平面AMC1，
连接MN，
在四边形CC1MN中，有MC1∥CN，同理得CN∥平面AMC1.
∵CN平面B1CN，B1N平面B1CN，CN∩B1N=N，∴平面AMC1∥平面NB1C.
（2）∵B1C1=A1C1，M为A1B1中点，∴C1M⊥A1B1，又三棱柱ABC-A1
B1C1侧棱A1A垂直于底面ABC，
∴A1A⊥CN，又CN∥C1M，∴A1A⊥C1M.又A1A∩A1B1=A1，∴C1M⊥平面AA1B1B.
又∵A1B平面AA1B1B，∴C1M⊥A1B，又AC1⊥A1B，AC1∩C1M=C1，∴A1B⊥平面AC1M.
∵AM平面AC1M，∴A1B⊥AM.
16.解：（1）连接SO，∵底面ABCD是菱形，O为AC与BD的交点，∴AC⊥BD.又SA=SC，
∴AC⊥SO.而SO∩BD=O，∴AC⊥平面SBD.
（2）取棱SC的中点M，CD的中点N，连接MN，则动点P的轨迹即是线段MN.证明如下：
连接EM，EN，∵E是BC中点，M是SC中点，∴EM∥SB，
同理EN∥BD.∵AC⊥平面SBD，∴AC⊥SB，∴AC⊥EM，同理AC⊥EN.
又EM∩EN=E，∴AC⊥平面EMN.因此，当P点在线段MN上运动时，总有PE⊥AC.
相关试卷
这是一份（数学理科）高考数学复习28 直线、平面的平行与垂直关系，共5页。
这是一份高考数学一轮复习作业本7.2 直线、平面的平行关系（含答案），共7页。
这是一份高考数学一轮复习检测：第7章第3节 直线、平面的垂直关系 含解析，共13页。
