





北师大版八年级下册3 三角形的中位线优秀精练
展开![]() 第六章 平行四边形
第六章 平行四边形
6.3 三角形的中位线

一、单选题
1.(2023·贵州六盘水·统考二模)如图,在![]() 中,D,E分别是
中,D,E分别是![]() 的中点,若
的中点,若![]() ,则
,则![]() 的长为( )
的长为( )
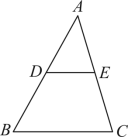
A.1 B.2 C.4 D.6
2.(2022春·八年级单元测试)如图,![]() ,
,![]() 两点被池塘隔开,在
两点被池塘隔开,在![]() 外选一点
外选一点![]() ,连接
,连接![]() ,
,![]() ,并分别找出它们的中点
,并分别找出它们的中点![]() ,
,![]() ,连接
,连接![]() ,现测得
,现测得![]() =
=![]() ,则
,则![]() 长为( )
长为( )
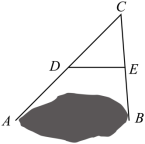
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(2023春·全国·八年级专题练习)如图每个小正方形的边长为![]() ,在
,在![]() 中,点
中,点![]() 分别为
分别为![]() 的中点,则线段
的中点,则线段![]() 的长为( )
的长为( )
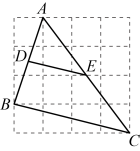
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(2023春·广东珠海·八年级珠海市紫荆中学校考期中)如图,![]() 是
是![]() 的中线,E、F分别是
的中线,E、F分别是![]() 的中点,连接
的中点,连接![]() .若
.若![]() ,则
,则![]() 的长为( )
的长为( )
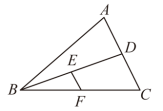
A.4 B.6 C.8 D.2
5.(2023春·北京西城·八年级北京市第一六一中学校考期中)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D,E分别是边
,点D,E分别是边![]() ,
,![]() 的中点,那么
的中点,那么![]() 的长为( )
的长为( )
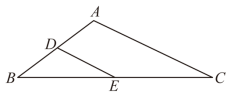
A.![]() B.2 C.3 D.4
B.2 C.3 D.4
6.(2023春·全国·八年级专题练习)如图所示,某居民小区为了美化居住环境,要在一块三角形![]() 空地上围一个四边形花坛
空地上围一个四边形花坛![]() .已知点
.已知点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,量得
的中点,量得![]() 米,则边
米,则边![]() 的长是( )
的长是( )
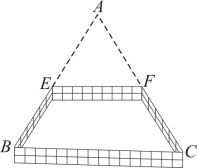
A.6米 B.7米 C.8米 D.9米
二、填空
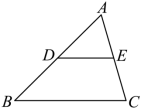
7.(2022秋·八年级单元测试)如图,在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点,若
边的中点,若![]() ,则
,则![]() 的长为______.
的长为______.
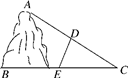
8.(2022春·湖南常德·八年级统考期中)如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,测得DE的长度为380米,则A,B两地之间的距离是________米.
9.(2023春·江苏·八年级期末)如图,在四边形![]() 中,
中,![]() ,
,![]() ,E,F,M分别为边
,E,F,M分别为边![]() ,
,![]() 和对角线
和对角线![]() 的中点.连接
的中点.连接![]() ,
,![]() ,则
,则![]() ____________.
____________.
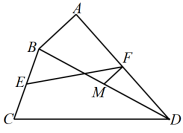
10.(2022春·辽宁本溪·八年级统考期末)如图,![]() ,
,![]() 是四边形
是四边形![]() 的对角线,点
的对角线,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,顺次连接
的中点,顺次连接![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() ,则四边形
,则四边形![]() 的周长是__________.
的周长是__________.
三、解答题(共0分
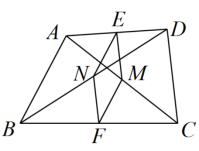
11.(2023春·浙江·八年级专题练习)已知:在![]() 中,D,E,F分别是边
中,D,E,F分别是边![]() 的中点.
的中点.
求证:四边形![]() 的周长等于
的周长等于![]() .
.
12.(2023春·江苏淮安·八年级校考期中)如图,点D、F分别为AC、BC的中点,![]() ,
,![]() ,求证:
,求证:![]()

一、填空题
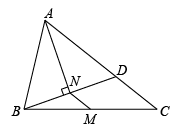
1.(2023春·陕西西安·八年级高新一中校考阶段练习)如图,![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]() 平分
平分![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的周长是__________.
的周长是__________.
2.(2022秋·八年级单元测试)如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,若
,若![]() ,则四边形
,则四边形![]() 的周长为______.
的周长为______.
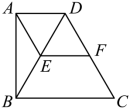
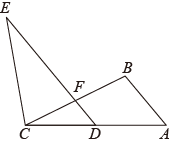
3.(2023·山东烟台·统考二模)如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的延长线上,F为
的延长线上,F为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,则
,则![]() 的长为__________.
的长为__________.
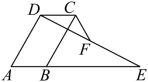
4.(2023春·浙江杭州·八年级校联考期中)如图,已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E、F分别是边
,点E、F分别是边![]() 、
、![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的长是 __.
的长是 __.
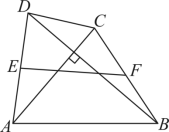
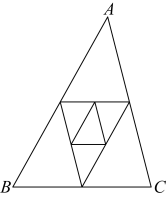
5.(2023秋·山东泰安·八年级校考期中)如图,已知![]() 的周长是1,连接
的周长是1,连接![]() 三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第
三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第![]() 个三角形的周长_______.
个三角形的周长_______.
二、解答题
6.(2022秋·八年级单元测试)如图所示,在四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点O,E,F分别是
交于点O,E,F分别是![]() 、
、![]() 的中点,且
的中点,且![]() .求证:
.求证:![]() .
.
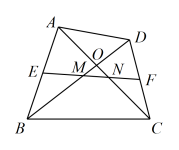
7.(2023春·浙江·八年级专题练习)如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 垂直平分
垂直平分![]() ;
;
(2)若![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,求
,求![]() 的长.
的长.
8.(2023·江苏扬州·统考二模)如图,D为等边三角形![]() 的边
的边![]() 延长线上一点,以
延长线上一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() 交
交![]() 于点F.
于点F.
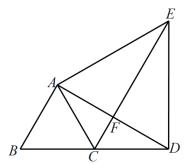
(1)求证:![]() ;
;
(2)若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
北师大版八年级下册第六章 平行四边形3 三角形的中位线同步测试题: 这是一份北师大版八年级下册<a href="/sx/tb_c94894_t7/?tag_id=28" target="_blank">第六章 平行四边形3 三角形的中位线同步测试题</a>,共7页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版八年级下册3 三角形的中位线课时训练: 这是一份初中数学北师大版八年级下册3 三角形的中位线课时训练,共8页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学北师大版八年级下册4 多边形的内角与外角和课时训练: 这是一份初中数学北师大版八年级下册4 多边形的内角与外角和课时训练,文件包含64多边形的内角和与外角和分层练习解析版docx、64多边形的内角和与外角和分层练习原卷版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。













