


所属成套资源:高考数学一轮复习夯基练习 (含答案)
高考数学一轮复习夯基练习:空间点、直线、平面之间的位置关系(含答案)
展开
这是一份高考数学一轮复习夯基练习:空间点、直线、平面之间的位置关系(含答案),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
夯基练习 空间点、直线、平面之间的位置关系一 、选择题1.如图,四面体PABC的六条棱均相等,D,E,F分别是AB,BC,CA的中点,则下列四个结论中不成立的是( )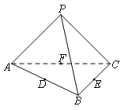 A.平面PDE⊥平面ABC B.DF⊥平面PAE C.BC∥平面PDF D.平面PAE⊥平面ABC
A.平面PDE⊥平面ABC B.DF⊥平面PAE C.BC∥平面PDF D.平面PAE⊥平面ABC
2.如图,在正方体ABCD-A1B1C1D1中,P是CD上的动点,则直线B1P与直线BC1所成的角为( )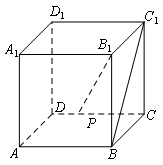
A.30° B.45° C.60° D.90°3.三条直线相交于一点,可能确定的平面有( ) A.1个 B.2个 C.3个 D.1个或3个4.如图,四棱锥P-ABCD的底面是边长为4的正方形,侧棱PA垂直于底面,且PA=3,则直线PC与平面ABCD所成角的正切值为( )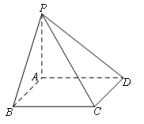 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )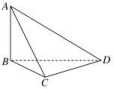 A. B.- C. D.- 6.在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC边的中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足=λ的实数λ的值有( )
A. B.- C. D.- 6.在正方体ABCD-A1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC边的中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足=λ的实数λ的值有( )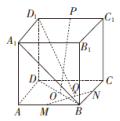 A.0个 B.1个 C.2个 D.3个 7.如图,正方体
A.0个 B.1个 C.2个 D.3个 7.如图,正方体![]() 中,P为线段
中,P为线段![]() 上的动点,则下列判断错误的是( )
上的动点,则下列判断错误的是( )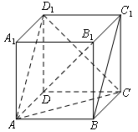 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]() 8.设α//β,A∈α,B∈β,C是AB的中点,当A,B分别在平面α,β内运动时,那么所有的动点C( ).A.不共面B.当且仅当A,B分别在两条直线上移动时才共面C.当且仅当A,B分别在两条给定的异面直线上移动时才共面D.不论A,B如何移动,都共面9.如图,在三棱锥S-ABC中,底面是边长为1的正三角形,O为△ABC的中心,侧棱长均为2,则侧棱与底面所成角的余弦值为( )
8.设α//β,A∈α,B∈β,C是AB的中点,当A,B分别在平面α,β内运动时,那么所有的动点C( ).A.不共面B.当且仅当A,B分别在两条直线上移动时才共面C.当且仅当A,B分别在两条给定的异面直线上移动时才共面D.不论A,B如何移动,都共面9.如图,在三棱锥S-ABC中,底面是边长为1的正三角形,O为△ABC的中心,侧棱长均为2,则侧棱与底面所成角的余弦值为( )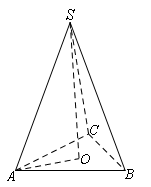
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.下列命题中,不正确的是( )①一条直线和两条平行直线都相交,那么这三条直线共面;②每两条都相交但不共点的四条直线一定共面;③两条相交直线上的三个点确定一个平面;④两条互相垂直的直线共面.A.①与② B.③与④ C.①与③ D.②与④11.如果直线a⊂平面α,直线b⊂平面α,M∈a,N∈b,M∈l,N∈l,则( ).A.l⊂α B.l⊄α C.l∩α=M D.l∩α=N12.如果直线a//平面α,那么直线a与平面α内的( ).A.一条直线不相交 B.两条相交直线不相交C.无数条直线不相交 D.任意一条直线不相交 二 、填空题13.已知直线l、m,平面α、β,则下列命题中是真命题的序号是_____.①若α∥β,l⊂α,则l∥β;②若α∥β,l⊥α,则l⊥β;③若l∥α,m⊂α,则l∥m;④若α⊥β,α∩β=l,m⊂α,m⊥l,则m⊥β. 14.已知α,β,γ是三个不同的平面,m,n是两条不同的直线,有下列三个条件:①m∥γ,n⊂β;②m∥γ,n∥β;③m⊂γ,n∥β.要使命题“若α∩β=m,n⊂γ,且_____,则m∥n”为真命题,则可以在横线处填入的条件是_____(把你认为正确条件的序号填上) 15.已知平面ɑ//β,P是平面ɑ,β外的一点,过点P的直线m与平面ɑ,β分别交于A,C两点,过点P的直线n与平面ɑ,β分别交于B,D两点,若PA=6,AC=9,PD=8,则BD的长为 . 16.如图所示,正方形![]() 所在平面与正方形
所在平面与正方形![]() 所在平面成60°的二面角,则异面直线
所在平面成60°的二面角,则异面直线![]() 与
与![]() 所成角的余弦值是_______.
所成角的余弦值是_______. 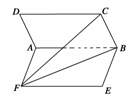 三 、解答题17.在直三棱柱ABCA1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.(1)求a的值;(2)求三棱锥B1A1BC的体积.
三 、解答题17.在直三棱柱ABCA1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.(1)求a的值;(2)求三棱锥B1A1BC的体积.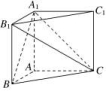 18.如图所示,A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.(1)求证:直线EF与BD是异面直线;(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
18.如图所示,A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.(1)求证:直线EF与BD是异面直线;(2)若AC⊥BD,AC=BD,求EF与BD所成的角.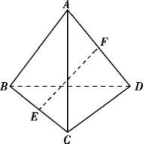 19.如图,已知ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP//GH.
19.如图,已知ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP//GH.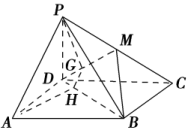 20.如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点.已知∠BAC=
20.如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点.已知∠BAC=![]() ,AB=2,AC=2
,AB=2,AC=2![]() ,PA=2.(1)求三棱锥P-ABC的体积;(2)求异面直线BC与AD所成角的余弦值.
,PA=2.(1)求三棱锥P-ABC的体积;(2)求异面直线BC与AD所成角的余弦值.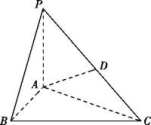
参考答案1.答案:A解题思路: 2.答案:D3.答案:D.4.答案:D解题思路:
2.答案:D3.答案:D.4.答案:D解题思路: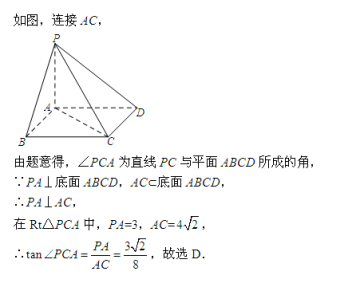 5.答案为:A;解析:如图,分别取AB,AD,BC,BD的中点E,F,G,O,连接EF,EG,OG,FO,FG,则EF∥BD,EG∥AC,所以∠FEG为异面直线AC与BD所成的角.易知FO∥AB,因为AB⊥平面BCD,所以FO⊥OG,设AB=2a,则EG=EF=a,FG==a,所以∠FEG=60°,所以异面直线AC与BD所成角的余弦值为,故选A.
5.答案为:A;解析:如图,分别取AB,AD,BC,BD的中点E,F,G,O,连接EF,EG,OG,FO,FG,则EF∥BD,EG∥AC,所以∠FEG为异面直线AC与BD所成的角.易知FO∥AB,因为AB⊥平面BCD,所以FO⊥OG,设AB=2a,则EG=EF=a,FG==a,所以∠FEG=60°,所以异面直线AC与BD所成角的余弦值为,故选A.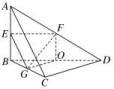 6.答案为:C;解析:本题可以转化为在MN上找点Q使OQ綊PD1,可知只有Q点与M,N重合时满足条件.故选C. 7.答案:D解题思路:
6.答案为:C;解析:本题可以转化为在MN上找点Q使OQ綊PD1,可知只有Q点与M,N重合时满足条件.故选C. 7.答案:D解题思路:
8.答案:D;解析:由面面平行的性质定理,点C应在过AB中点且平行于α(或β)的平面内.故选D.9.答案:D解题思路:
10.答案:B.11.答案:A;解析:据公理1可知:直线l上两点M、N都在平面α内,所以l在平面α内,故选A.12.答案:D;解析:线面平行,则线面无公共点,所以选D,对于C,要注意“无数”并不代表所有. 二 、填空题13.答案为:①②④;14.答案为:③或①;15.答案:24或4.8.16.答案为:![]() ; 三 、解答题17.解:(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,即∠A1BC=60°.又AA1⊥平面ABC,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,由AB=AC=1,∠BAC=90°⇒BC=,∴A1B=⇒=⇒a=1.(2)∵CA⊥A1A,CA⊥AB,A1A∩AB=A,∴CA⊥平面A1B1B,∴VB1A1BC=VCA1B1B=××1=. 18.解析:(1)证明:假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内,这与A是△BCD所在平面外的一点相矛盾.故直线EF与BD是异面直线.(2)取CD的中点G,连接EG,FG,则AC∥FG,EG∥BD,所以相交直线EF与EG所成的角(或其补角)即为异面直线EF与BD所成的角.
; 三 、解答题17.解:(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,即∠A1BC=60°.又AA1⊥平面ABC,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,由AB=AC=1,∠BAC=90°⇒BC=,∴A1B=⇒=⇒a=1.(2)∵CA⊥A1A,CA⊥AB,A1A∩AB=A,∴CA⊥平面A1B1B,∴VB1A1BC=VCA1B1B=××1=. 18.解析:(1)证明:假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内,这与A是△BCD所在平面外的一点相矛盾.故直线EF与BD是异面直线.(2)取CD的中点G,连接EG,FG,则AC∥FG,EG∥BD,所以相交直线EF与EG所成的角(或其补角)即为异面直线EF与BD所成的角.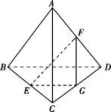 又因为AC⊥BD,AC=BD,则FG⊥EG,FG=EG.所以∠FEG=45°,即异面直线EF与BD所成的角为45°. 19.
又因为AC⊥BD,AC=BD,则FG⊥EG,FG=EG.所以∠FEG=45°,即异面直线EF与BD所成的角为45°. 19.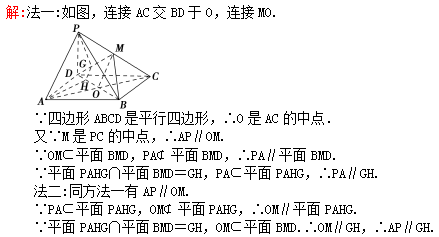 20.解析:(1)因为PA⊥底面ABC,所以PA是三棱锥P-ABC的高.又S△ABC=
20.解析:(1)因为PA⊥底面ABC,所以PA是三棱锥P-ABC的高.又S△ABC=![]() ×2×2
×2×2![]() =2
=2![]() ,所以三棱锥P-ABC的体积为V=
,所以三棱锥P-ABC的体积为V=![]() S△ABC·PA=
S△ABC·PA=![]() ×2
×2![]() ×2=
×2=![]() .(2)如图,取PB的中点E,连接DE,AE,则ED∥BC,所以∠ADE(或其补角)是异面直线BC与AD所成的角.
.(2)如图,取PB的中点E,连接DE,AE,则ED∥BC,所以∠ADE(或其补角)是异面直线BC与AD所成的角.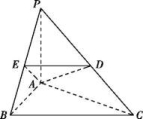 易知PB=2
易知PB=2![]() ,PC=4,BC=4,则在△ADE中,DE=2,AE=
,PC=4,BC=4,则在△ADE中,DE=2,AE=![]() ,AD=2,所以cos∠ADE=
,AD=2,所以cos∠ADE=![]() =
=![]() .故异面直线BC与AD所成角的余弦值为
.故异面直线BC与AD所成角的余弦值为![]() .
.
相关试卷
这是一份高考数学一轮复习夯基练习:直线与圆、圆与圆的位置关系(含答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习夯基练习:直线、平面平行的判定及其性质(含答案),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份高考数学一轮复习夯基练习:直线、平面垂直的判定及其性质(含答案),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









