高考数学一轮复习夯基练习：解三角形应用举例(含答案)

这是一份高考数学一轮复习夯基练习：解三角形应用举例(含答案)，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
夯基练习 解三角形应用举例一 、选择题1.海上有三个小岛A，B，C，测得∠BAC=135°，AB=6，AC=3，若在B，C两岛的连线段之间建一座灯塔D，使得灯塔D到A，B两岛距离相等，则B，D间的距离为(　　)A．3          B．           C．          D．3  2.有一长为1公里的斜坡，它的倾斜角为20°，现要将倾斜角改成10°，则斜坡长为(　　)A．1           B．2sin 10°           C．2cos 10°           D．cos 20°  3.一个大型喷水池的中央有一个强大喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进100 m到达点B，在B点测得水柱顶端的仰角为30°，则水柱的高度是(　　)A．50 m            B．100 m           C．120 m           D．150 m  4.如图，为了测量A，C两点间的距离，选取同一平面上B，D两点，测出四边形ABCD各边的长度(单位：km)．AB=5，BC=8，CD=3，DA=5，且∠B与∠D互补，则AC的长为(　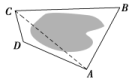　)A．7 km            B．8 km           C．9 km            D．6 km  5.在△ABC中，三边a，b，c与面积S的关系式为a2＋4S=b2＋c2，则角A为(　　)A．45°        B．60°        C．120°        D．150°  6.两灯塔A、B与海洋观察站C的距离都等于2 km，灯塔A在观察站C的北偏东30°，灯塔B在观察站C南偏东60°，则A、B之间的距离为(　　)A．2 km            B．3 km           C．4 km            D．5 km  7.在静水中划船的速度是每分钟40 m，水流的速度是每分钟20 m，如果船从岸边A处出发，沿着与水流垂直的航线到达对岸，那么船前进的方向指向河流的上游并与河岸垂直的方向所成的角为(　　)A.         B.         C.         D.π  8.在△ABC中，已知AB=，AC=，tan∠BAC=－3，则BC边上的高等于(　　)A．1             B.          C.            D．2  9.如图，四边形ABCD中，B=C=120°，AB=4，BC=CD=2，则该四边形的面积等于(　　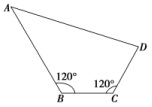)A.         B．5         C．6         D．7  10.在△ABC中，若cos B=，=2，且S△ABC=，则b等于(　　)A．4         B．3        C．2         D．1  11.在某个位置测得某山峰仰角为θ，对着山峰在地面上前进600 m后测得仰角为2θ，继续在地面上前进200 m以后测得山峰的仰角为4θ，则该山峰的高度为(　　)A．200 m          B．300 m          C．400 m          D．100 m  12.在△ABC中，sin2A≤sin2B＋sin2C－sin Bsin C，则A的取值范围是(　　)A.        B.        C.         D.   二 、填空题13.某海岛周围38海里有暗礁，一轮船由西向东航行，初测此岛在北偏东60°方向，航行30海里后测得此岛在东北方向，若不改变航向，则此船________触礁的危险(填“有”或“无”)．解析：由题意在三角形ABC中，AB=30，∠BAC=30°，∠ABC=135°，∴∠ACB=15°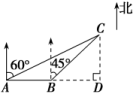，  14.如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°.已知山高BC=100 m，则山高MN=________m. 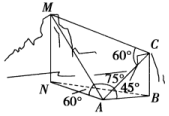 15.已知两座灯塔A和B与海洋观察站C的距离相等，灯塔A在观察站C的北偏东40°，灯塔B在观察站C的南偏东60°，则灯塔A在灯塔B的________．  16.如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD=____________m. 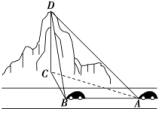  三 、解答题17.要测量对岸两点A、B之间的距离，选取相距 km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°，求A、B之间的距离．                  18.为保障高考的公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1千米处不能收到手机信号，检查员抽查青岛市一考点，在考点正西约1.732千米有一条北偏东60°方向的公路，在此处检查员用手机接通电话，以每小时12千米的速度沿公路行驶，问最长需要多少分钟，检查员开始收不到信号，并至少持续多长时间该考点才算合格？                 19.在某海域A处正东方向相距80海里的B处有一艘客轮遇险，在原地等待救援．信息中心立即把消息告知在其南偏西30°，相距40海里的C处的救援船，救援船立即朝北偏东θ角的方向沿直线CB前往B处救援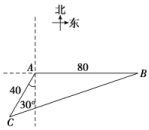．(1)若救援船的航行速度为60海里/小时，求救援船到达客轮遇险位置的时间；(2)求tan θ的值．              20.如图，为了测量河的宽度，在一岸边选定两点A，B，望对岸的标记物C，测得∠CAB=45°，∠CBA=75°，AB=120米，求河的宽度．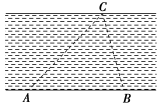            
参考答案1.答案为：B；解析：由题意可知，D为线段AB的垂直平分线与BC的交点，设BD=t．由余弦定理可得BC2=62＋(3)2－2×6×3cos∠BAC=90，解得BC=3．由cos∠ABC==，解得t=．故选B．  2.答案为：C；解析：原来的斜坡、覆盖的地平线及新的斜坡构成等腰三角形，这个等腰三角形的底边长就是所求．  3.答案为：A.解析：作出示意图如图所示，设水柱高度是hm，水柱底端为C，则在△ABC中，A=60°，AC=h，AB=100，在Rt△BCD中，BC=h，根据余弦定理得，(h)2=h2＋1002－2·h·100·cos 60°，即h2＋50h－5 000=0，即(h－50)(h＋100)=0，即h=50，故水柱的高度是50 m.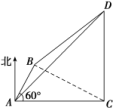  4.答案为：A.解析：在△ACD中，由余弦定理得：cos D==.在△ABC中，由余弦定理得：cos B==.因为∠B＋∠D=180°，所以cos B＋cos D=0，即＋=0，解得AC=7.  5.答案为：A；解析：4S=b2＋c2－a2=2bccos A，所以4·bcsin A=2bccos A，所以tan A=1，又因为A∈(0°，180°)，所以A=45°.  6.答案为：C；解析：如下图所示，∠ACB=90°，又AC=BC=2，在△ABC中由勾股定理得：AB===4. 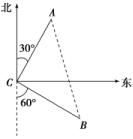 7.答案为：C；解析：设水流速度与船速的合速度为v，方向指向对岸．则由题意知，sin α===，又α∈，所以α=. 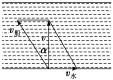 8.答案为：A；解析：因为tan∠BAC=－3，所以sin∠BAC=，cos∠BAC=－.由余弦定理，得BC2=AC2＋AB2－2AC·ABcos∠BAC=5＋2－2×××=9，所以BC=3，所以S△ABC=AB·ACsin∠BAC=×××=，所以BC边上的高h===1，故选A.  9.答案为：B；解析：连接BD(图略)，在△BCD中，由已知条件，知∠DBC==30°，∴∠ABD=90°.在△BCD中，由余弦定理BD2=BC2＋CD2－2BC·CDcos C，知BD2=22＋22－2×2×2cos 120°=12，∴BD=2，∴S四边形ABCD=S△ABD＋S△BCD=×4×2＋×2×2×sin 120°=5.  10.答案为：C；解析：依题意得：c=2a，b2=a2＋c2－2accos B=a2＋(2a)2－2×a×2a×=4a2，所以b=c=2a.因为B∈(0，π)，所以sin B==，又S△ABC=acsin B=××b×=，所以b=2.  11.答案为：B；解析：如下图所示，△BED，△BDC为等腰三角形，BD=ED=600，BC=DC=200.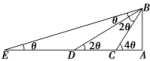在△BCD中，由余弦定理可得cos 2θ==，所以2θ=30°，4θ=60°.在Rt△ABC中，AB=BC·sin 4θ=200×=300(cm)．  12.答案为：C；解析：由正弦定理及sin2A≤sin2B＋sin2C－sin Bsin C可得a2≤b2＋c2－bc，即b2＋c2－a2≥bc，由余弦定理可得cos A=≥=，又0<A<π，所以0<A≤.故A的取值范围是.故选C.   二 、填空题13.答案为：无；由正弦定理：BC=·sin∠BAC=·sin 30°==15(＋)．在Rt△BDC中，CD=BC=15(＋1)＞38.  14.答案为：150；解析：根据图示，AC=100.在△MAC中，∠CMA=180°－75°－60°=45°.由正弦定理得=⇒AM=100.在△AMN中，=sin 60°，所以MN=100×=150 (m)．  15.答案为：北偏西10°；解析：如下图所示，因为AC=BC，所以∠CAB=∠CBA.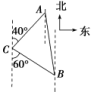又∠ACB=180°－40°－60°=80°，所以∠CAB=∠CBA=50°.故A在B的北偏西10°的方向．  16.答案为：100；解析：依题意，∠BAC=30°，∠ABC=105°，在△ABC中，由∠ABC＋∠BAC＋∠ACB=180°，所以∠ACB=45°，因为AB=600，由正弦定理可得=，即BC=300m，在Rt△BCD中，因为∠CBD=30°，BC=300.所以tan 30°==，所以CD=100m.   三 、解答题17.解：如图所示，在△ACD中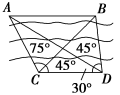，∠ACD=120°，∠CAD=∠ADC=30°，所以AC=CD= (km)．在△BCD中，∠BCD=45°，∠BDC=75°，∠CBD=60°，所以BC==( km)．在△ABC中，由余弦定理得AB2=()2＋－2××cos 75°=3＋2＋－=5，所以AB=(km)．所以A、B之间的距离为 km.  18.解：如图所示，考点为A，检查开始处为B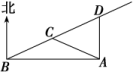，设公路上C、D两点到考点的距离为1千米．在△ABC中，AB=≈1.732，AC=1，∠ABC=30°，由正弦定理sin∠ACB=·AB=，∴∠ACB=120°(∠ACB=60°不合题意)，∴∠BAC=30°，∴BC=AC=1，在△ACD中，AC=AD，∠ACD=60°，∴△ACD为等边三角形，∴CD=1，∴×60=5，∴在BC上需5分钟，CD上需5分钟．答：最长需要5分钟检查员开始收不到信号，并持续至少5分钟才算合格．  19.解：(1)在题图中的△ABC中，AB=80，AC=40，∠BAC=120°，由余弦定理可知：BC2=AB2＋AC2－2AB·AC·cos 120°，即BC2=802＋402－2·80·40·=11 200，故BC=40，故救援船到达客轮遇险位置所需时间为=小时．(2)在△ABC中，由正弦定理可得=⇒sin∠ACB=sin∠BAC=，显然∠ACB为锐角，故cos∠ACB=，tan∠ACB=，而θ=∠ACB＋30°.故tan θ=tan(∠ACB＋30°)==.  20.解：在△ABC中，∵∠CAB=45°，∠CBA=75°，∴∠ACB=60°.由正弦定理，可得AC===20(3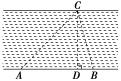＋)，设C到AB的距离为CD，则CD=ACsin∠CAB=AC=20 (＋3)．∴河的宽度为20(＋3)米．