


还剩6页未读,
继续阅读
成套系列资料,整套一键下载
2023七年级数学下册第七章相交线与平行线专项2平行线中的拐点问题上课课件新版冀教版
展开
这是一份2023七年级数学下册第七章相交线与平行线专项2平行线中的拐点问题上课课件新版冀教版,共12页。
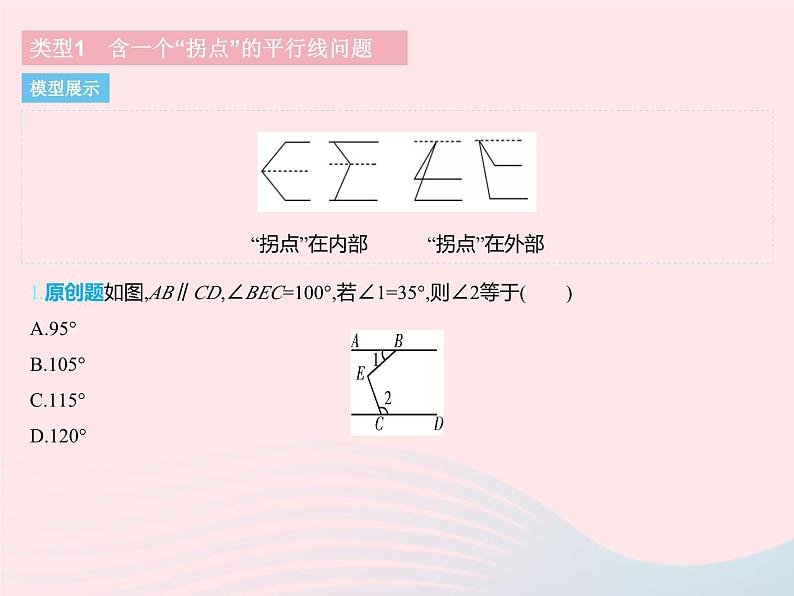
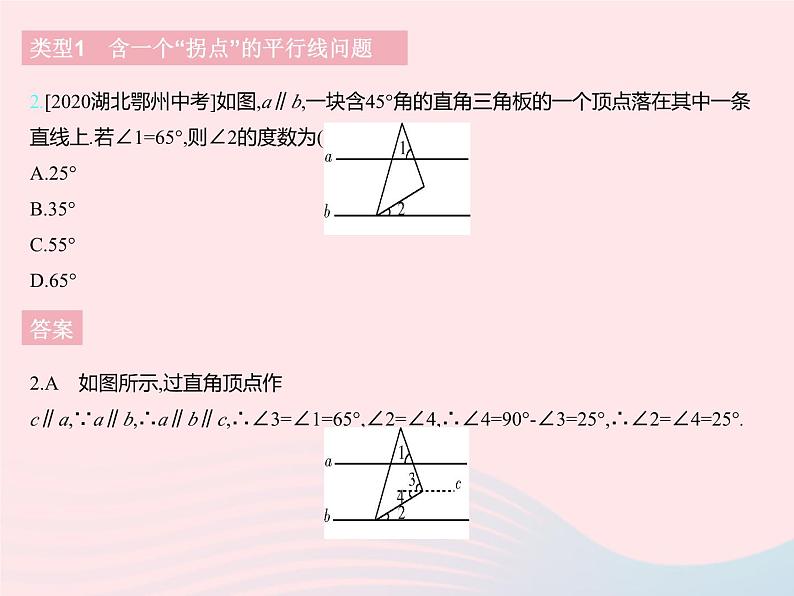
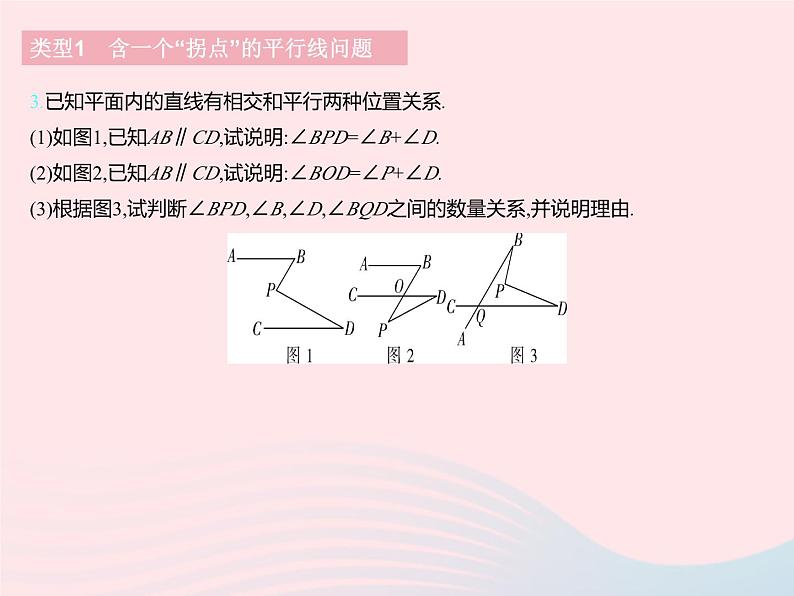
专项2 平行线中的“拐点”问题“拐点”在内部 “拐点”在外部类型1 含一个“拐点”的平行线问题模型展示1.原创题如图,AB∥CD,∠BEC=100°,若∠1=35°,则∠2等于( ) A.95° B.105°C.115° D.120°类型1 含一个“拐点”的平行线问题答案1.C 如图,过点E作EF∥AB.又∵AB∥CD,∴AB∥EF∥CD,∴∠2+∠FEC=180°,∠BEF=∠1=35°.又∵∠BEC=100°,∴∠FEC=∠BEC-∠BEF=100°-35°=65°,∴∠2=180°-∠FEC=180°-65°=115°.2.[2020湖北鄂州中考]如图,a∥b,一块含45°角的直角三角板的一个顶点落在其中一条直线上.若∠1=65°,则∠2的度数为( )A.25° B.35° C.55° D.65°类型1 含一个“拐点”的平行线问题答案2.A 如图所示,过直角顶点作c∥a,∵a∥b,∴a∥b∥c,∴∠3=∠1=65°,∠2=∠4,∴∠4=90°-∠3=25°,∴∠2=∠4=25°.3.已知平面内的直线有相交和平行两种位置关系.(1)如图1,已知AB∥CD,试说明:∠BPD=∠B+∠D.(2)如图2,已知AB∥CD,试说明:∠BOD=∠P+∠D.(3)根据图3,试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.类型1 含一个“拐点”的平行线问题类型1 含一个“拐点”的平行线问题答案3.解:(1)过点P作PE∥AB,如图1所示.因为AB∥PE,(辅助线)AB∥CD,(已知)所以AB∥PE∥CD.(在同一平面内,平行于同一直线的两条直线互相平行)所以∠B=∠BPE,∠D=∠DPE,(两直线平行,内错角相等)所以∠BPD=∠BPE+∠DPE=∠B+∠D.(等量代换)(2)过点P作PE∥CD,如图2所示.因为PE∥CD,(辅助线)所以∠BOD=∠BPE,(两直线平行,同位角相等)∠D=∠DPE,(两直线平行,内错角相等)所以∠BOD=∠BPE=∠BPD+∠DPE=∠BPD+∠D.(等量代换) 类型1 含一个“拐点”的平行线问题答案(3)数量关系:∠BPD=∠BQD+∠B+∠D.理由如下:过点P作PE∥CD,过点B作BF∥PE,如图3所示.则BF∥PE∥CD,所以∠FBA+∠BQD=180°,∠FBP+∠BPE=180°,(两直线平行,同旁内角互补)∠D=∠DPE,(两直线平行,内错角相等)又因为∠FBA=∠FBP+∠PBA,所以∠FBP+∠PBA+∠BQD=180°,180°-∠BPE+∠PBA+∠BQD=180°,所以∠BPE=∠BQD+∠PBA,所以∠BPD=∠BPE+∠DPE=∠BQD+∠PBA+∠D.(等量代换)4.如图,已知AB∥CD,∠1=∠2.试说明:∠BEF=∠EFC.类型2 含多个“拐点”的平行线问题答案4.解:解法一 如图,分别过点E,F作EM∥AB,NF∥CD,易知AB∥EM∥NF∥CD,∴∠1=∠BEM,∠MEF=∠EFN,∠NFC=∠2,∵∠1=∠2,∴∠BEF=∠BEM+∠MEF=∠2+∠EFN=∠NFC+∠EFN=∠EFC,即∠BEF=∠EFC.类型2 含多个“拐点”的平行线问题答案解法二 如图,连接BC,∵AB∥CD,∴∠ABC=∠DCB,又∠1=∠2,∴∠EBC=∠FCB,∴BE∥CF,∴∠BEF=∠EFC. 解法三 如图,延长BE交DC的延长线于点H.∵AB∥CD,∴∠1=∠H.∵∠1=∠2,∴∠H=∠2,∴BH∥FC,∴∠BEF=∠EFC.5.[2021河北邢台期中]如图,点A、B分别在直线CM,DN上,CM∥DN.(1)如图1,连接AB,则∠CAB+∠ABD= °; (2)如图2,点P1是直线CM,DN内部的一个点,连接AP1,BP1.试说明:∠CAP1+∠AP1B+∠P1BD=360°;(3)如图3,点P1,P2是直线CM,DN内部两个不重合的点,连接AP1,P1P2,P2B.试求∠CAP1+∠AP1P2+∠P1P2B+∠P2BD的度数;(4)若按以上规律,猜想并直接写出∠CAP1+∠AP1P2+‧‧‧+∠P5BD的度数(不必写出过程).类型2 含多个“拐点”的平行线问题类型2 含多个“拐点”的平行线问题答案5.解:(1)180.(2)如图1,过点P1作EP1∥CM,易知CM∥EP1∥DN,∴∠AP1E+∠CAP1=180°,∠EP1B+∠P1BD=180°,∴∠CAP1+∠AP1B+∠P1BD=∠CAP1+∠AP1E+∠EP1B+∠P1BD=180°+180°=360°. (3)如图2,过点P1作EP1∥CM,过点P2作FP2∥DN,易知CM∥EP1∥FP2∥DN,∴∠AP1E+∠CAP1=180°,∠EP1P2+∠P1P2F=180°,∠FP2B+∠P2BD=180°,∴∠CAP1+∠AP1P2+∠P1P2B+∠P2BD=∠CAP1+∠AP1E+∠EP1P2+∠P1P2F+∠FP2B+∠P2BD=3×180°=540°.(4)∠CAP1+∠AP1P2+‧‧‧+∠P5BD=6×180°=1 080°.
专项2 平行线中的“拐点”问题“拐点”在内部 “拐点”在外部类型1 含一个“拐点”的平行线问题模型展示1.原创题如图,AB∥CD,∠BEC=100°,若∠1=35°,则∠2等于( ) A.95° B.105°C.115° D.120°类型1 含一个“拐点”的平行线问题答案1.C 如图,过点E作EF∥AB.又∵AB∥CD,∴AB∥EF∥CD,∴∠2+∠FEC=180°,∠BEF=∠1=35°.又∵∠BEC=100°,∴∠FEC=∠BEC-∠BEF=100°-35°=65°,∴∠2=180°-∠FEC=180°-65°=115°.2.[2020湖北鄂州中考]如图,a∥b,一块含45°角的直角三角板的一个顶点落在其中一条直线上.若∠1=65°,则∠2的度数为( )A.25° B.35° C.55° D.65°类型1 含一个“拐点”的平行线问题答案2.A 如图所示,过直角顶点作c∥a,∵a∥b,∴a∥b∥c,∴∠3=∠1=65°,∠2=∠4,∴∠4=90°-∠3=25°,∴∠2=∠4=25°.3.已知平面内的直线有相交和平行两种位置关系.(1)如图1,已知AB∥CD,试说明:∠BPD=∠B+∠D.(2)如图2,已知AB∥CD,试说明:∠BOD=∠P+∠D.(3)根据图3,试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.类型1 含一个“拐点”的平行线问题类型1 含一个“拐点”的平行线问题答案3.解:(1)过点P作PE∥AB,如图1所示.因为AB∥PE,(辅助线)AB∥CD,(已知)所以AB∥PE∥CD.(在同一平面内,平行于同一直线的两条直线互相平行)所以∠B=∠BPE,∠D=∠DPE,(两直线平行,内错角相等)所以∠BPD=∠BPE+∠DPE=∠B+∠D.(等量代换)(2)过点P作PE∥CD,如图2所示.因为PE∥CD,(辅助线)所以∠BOD=∠BPE,(两直线平行,同位角相等)∠D=∠DPE,(两直线平行,内错角相等)所以∠BOD=∠BPE=∠BPD+∠DPE=∠BPD+∠D.(等量代换) 类型1 含一个“拐点”的平行线问题答案(3)数量关系:∠BPD=∠BQD+∠B+∠D.理由如下:过点P作PE∥CD,过点B作BF∥PE,如图3所示.则BF∥PE∥CD,所以∠FBA+∠BQD=180°,∠FBP+∠BPE=180°,(两直线平行,同旁内角互补)∠D=∠DPE,(两直线平行,内错角相等)又因为∠FBA=∠FBP+∠PBA,所以∠FBP+∠PBA+∠BQD=180°,180°-∠BPE+∠PBA+∠BQD=180°,所以∠BPE=∠BQD+∠PBA,所以∠BPD=∠BPE+∠DPE=∠BQD+∠PBA+∠D.(等量代换)4.如图,已知AB∥CD,∠1=∠2.试说明:∠BEF=∠EFC.类型2 含多个“拐点”的平行线问题答案4.解:解法一 如图,分别过点E,F作EM∥AB,NF∥CD,易知AB∥EM∥NF∥CD,∴∠1=∠BEM,∠MEF=∠EFN,∠NFC=∠2,∵∠1=∠2,∴∠BEF=∠BEM+∠MEF=∠2+∠EFN=∠NFC+∠EFN=∠EFC,即∠BEF=∠EFC.类型2 含多个“拐点”的平行线问题答案解法二 如图,连接BC,∵AB∥CD,∴∠ABC=∠DCB,又∠1=∠2,∴∠EBC=∠FCB,∴BE∥CF,∴∠BEF=∠EFC. 解法三 如图,延长BE交DC的延长线于点H.∵AB∥CD,∴∠1=∠H.∵∠1=∠2,∴∠H=∠2,∴BH∥FC,∴∠BEF=∠EFC.5.[2021河北邢台期中]如图,点A、B分别在直线CM,DN上,CM∥DN.(1)如图1,连接AB,则∠CAB+∠ABD= °; (2)如图2,点P1是直线CM,DN内部的一个点,连接AP1,BP1.试说明:∠CAP1+∠AP1B+∠P1BD=360°;(3)如图3,点P1,P2是直线CM,DN内部两个不重合的点,连接AP1,P1P2,P2B.试求∠CAP1+∠AP1P2+∠P1P2B+∠P2BD的度数;(4)若按以上规律,猜想并直接写出∠CAP1+∠AP1P2+‧‧‧+∠P5BD的度数(不必写出过程).类型2 含多个“拐点”的平行线问题类型2 含多个“拐点”的平行线问题答案5.解:(1)180.(2)如图1,过点P1作EP1∥CM,易知CM∥EP1∥DN,∴∠AP1E+∠CAP1=180°,∠EP1B+∠P1BD=180°,∴∠CAP1+∠AP1B+∠P1BD=∠CAP1+∠AP1E+∠EP1B+∠P1BD=180°+180°=360°. (3)如图2,过点P1作EP1∥CM,过点P2作FP2∥DN,易知CM∥EP1∥FP2∥DN,∴∠AP1E+∠CAP1=180°,∠EP1P2+∠P1P2F=180°,∠FP2B+∠P2BD=180°,∴∠CAP1+∠AP1P2+∠P1P2B+∠P2BD=∠CAP1+∠AP1E+∠EP1P2+∠P1P2F+∠FP2B+∠P2BD=3×180°=540°.(4)∠CAP1+∠AP1P2+‧‧‧+∠P5BD=6×180°=1 080°.
相关资料
更多









