北师大版九年级下册1 二次函数导学案

5.2二次函数的图像和性质

一、问题导学：

1、二次函数的图像的特征是________________；由此可以得出二次函数的图象的对称轴是轴（或顶点在轴上）的条件是______。

2、若二次函数的图像经过原点，将（0，0）代入函数解析式得_____；由此可以得出二次函数的图像经过原点的条件是__________。

3、二次函数的图像与_____轴必有一个交点，此交点坐标是_____。c决定抛物线与y轴交点P(0,c)的位置，当c______， P在y轴正半轴上；c______，P在原点；c______，P在y轴负半轴。：

4、二次函数的图像的特征是________________；此时抛物线与轴只有一个公共点，由此可以得出二次函数的图象顶点在轴上的条件是____________。

二、探究，小结归纳：

1、确定a、b、c的符号

(1)二次函数：， a的符号由________决定；

(2) 的符号由________决定，结合a的符号，可确定______的符号；

(3)c的符号由_________________决定，当抛物线与y轴交点在y轴的正半轴时，c_____，当抛物线与y轴交点在y轴的负半轴时，c______。

(4)确定了a、b、c的符号，易确定abc的符号。

2、确定类似代数式a+b+c的符号

当x=1时， y=a+b+c。因此代数式a+b+c的符号由__________________________决定；与之类似的还经常出现判断a-b+c 、4a±2b+c、9a±3b+c等等的符号。

3、、由对称轴x=的确定值判断a与b的关系。

涉及到2a和b的代数式时常考虑对称轴x=的位置情况。如：=1能判断出：a = b，即。

三、例题讲解：

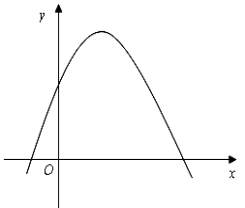
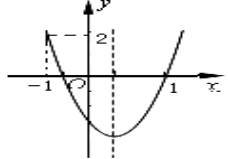
例1、如图，给出八个结论：①a＞0；②b＞0；③c＞0； ④a+b+c=0；⑤abc＜0；⑥2a+ b＞0；(7)a+c=1；⑧a＞1．其中正确的结论的序号是     ____________________ 。

四、练习：

1.二次函数的图像如图，则点M（b ，）在第_______象限。

2．二次函数y=x2+2x-3的图象的对称轴是直线                ．

3．已知二次函数y=x2+bx+3的对称轴为x=2，则b=             ．

4．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

则它的开口方向(  )  ，对称轴为  (  )  ．

5．已知抛物线y=ax2+bx+c经过点A（-2，7）、B（6，7）、C（3，-8），则该抛物线上纵坐标为-8的另一点坐标为           ．

6．已知a＜0，b＞0，那么抛物线y=ax2+bx+2的顶点在（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

7．如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（　　）

A．8 B．14 C．8或14 D．-8或-14

8．过原点的抛物线的解析式是（　　）

A．y=3x2-1 B．y=3x2+1 C．y=3（x+1）2 D．y=3x2+x

9．已知二次函数y=mx2+x+m（m-2）的图象经过原点，则m的值为（　　）

A．0或2 B．0 C．2 D．无法确定

10．二次函数y=x2+2x-5取最小值时，自变量x的值是（　　）

A．2 B．-2 C．1 D．-1

11．二次函数y=x2-2x+2有（　　）

A．最大值1 B．最大值2 C．最小值1 D．最小值2

12．二次函数y=x2-8x+c的最小值是0，那么c的值等于（　　）

A．4 B．8 C．-4 D．16

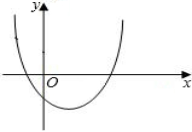
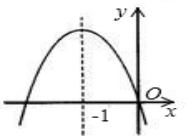
13．二次函数y=ax2+bx+c的图象如图所示，下列结论错误的是（　　）

A．a＞0 B．b＞0 C．c＜0 D．abc＞0

14．二次函数y=ax2+bx+c的图象过原点，且与x轴的正半轴相交，则下列各式正确的（　　）

A．a＞0，b＜0，c＜0 B．c=0，ab＜0

C．a≠0，b＜0，c=0 D．a≠0，b≥0，c=0

15．已知二次函数y=ax2+bx+c的图象如图所示，下列结论：①a+b+c＞0；②a-b+c＞0；③abc＜0；④2a+b=0．其中正确的个数为（　　）

A．1个 B．2个 C．3个 D．4个

16．二次函数y=-x2+bx+c，若b+c=0，则它的图象一定过点（　　）

A．（-1，1） B．（1，-1） C．（-1，-1） D．（1，1）

17．已知：抛物线y=ax2+bx+c（a＜0）经过点（-1，0），且满足4a+2b+c＞0，以下结论：①a+b＞0；②a+c＞0；③-a+b+c＞0；④b2-2ac＞5a2，其中正确的个数有（　　）

A．1个 B．2个 C．3个 D．4个

18．已知a＜-1，点（a-1，y1），（a，y2），（a+1，y3）都在函数y=x2的图象上，则（　　）

A．y1＜y2＜y3 B．y1＜y3＜y2 C．y3＜y2＜y1 D．y2＜y1＜y3

19．抛物线y=-2（x-1）2-3与y轴的交点纵坐标为（　　）

A．-3 B．-4 C．-5 D．-1

20．将函数y=x2+x的图象向右平移a（a＞0）个单位，得到函数y=x2-3x+2的图象，则a的值为（　　）

A．1 B．2 C．3 D．4

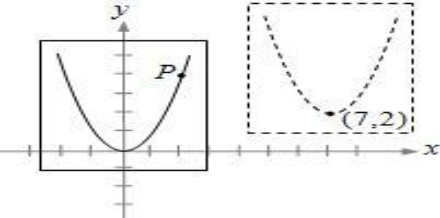
21．如图，坐标平面上有一透明片，透明片上有一拋物线及一点P，且拋物线为二次函数y=x2的图形，P的坐标（2，4）．若将此透明片向右、向上移动后，得拋物线的顶点坐标为（7，2），则此时P的坐标为何（　　）

A．（9，4） B．（9，6） C．（10，4） D．（10，6）

22．把抛物线y=-x2-2平移后得到抛物线y=-x2，平移的方法可以是（　　）

A．沿y轴向上平移2个单位 B．沿y轴向下平移2个单位

C．沿x轴向右平移2个单位 D．沿x轴向左平移2个单位

23．由函数y=- x2的图象平移得到函数y=-（x-4）2+5的图象，则这个平移是（　　）

A．先向左平移4个单位，再向下平移5个单位

 B．先向左平移4个单位，再向上平移5个单位

C．先向右平移4个单位，再向下平移5个单位 

 D．先向右平移4个单位，再向上平移5个单位

24．已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（　　）

A．抛物线开口向上

B．抛物线与y轴交于负半轴

C．当x=4时，y＞0

D．方程ax2+bx+c=0的正根在3与4之间

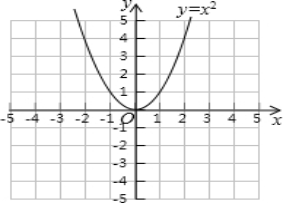
25．二次函数y=x2的图象如图所示，请将此图象向右平移1个单位，再向下平移2个单位．

（1）画出经过两次平移后所得到的图象，并写出函数的解析式；

（2）求经过两次平移后的图象与x轴的交点坐标，指出当x满足什么条件时，函数值大于0？

26．由表格中信息可知，若设y=ax2+bx+c，则下列y与x之间的函数关系式正确的是（　　）

A．y=x2-4x+3 B．y=x2-3x+4 C．y=x2-3x+3 D．y=x2-4x+8

27.求经过点（-1，6）、(2，5)，（1，2）三点的抛物线的解析式。

28.抛物线y=ax2+bx+c过（-1，-22），（0，8），（2，8）三点，求它的开口方向、对称轴和顶点坐标。

29.已知二次函数的顶点坐标为（3，-2）且过（2，－）求函数解析式。　

30.求与x轴两个交点分别为（-5，0）、(1，0)，且经过点（-4，5）的抛物线的解析式。