2023年河北省唐山市丰润区中考数学二模试卷（含解析）

这是一份2023年河北省唐山市丰润区中考数学二模试卷（含解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 如图，将△ABC折叠，使点C落在BC边上，展开后得到折痕AD，则AD是△ABC的( )
A. 高线B. 中线C. 垂线D. 角平分线
2. 如图，a/​/b，则下列结论中，不一定正确的是( )
A. ∠4=∠5
B. ∠1+∠2=180°
C. ∠2+∠3=180°
D. ∠2+∠4=180°
3. 如图，光线由上向下照射正五棱柱时的正投影是( )
A.
B.
C.
D.
4. 位于四川省的三星堆遗址被称为20世纪人类最伟大的考古发现之一，其中出土的文物是宝贵的人类文化遗产，在中国的文物群体中，属最具历史、科学、文化、艺术价值和最富观赏性的文物群体之一.下列四个图案是三星堆遗址出土文物图，其中是中心对称图形的是( )
A. B.
C. D.
5. 如图是小明某一天测得的7次体温情况的折线统计图，下列信息不正确的是( )
A. 测得的最高体温为37.1℃B. 前3次测得的体温在下降
C. 这组数据的众数是36.8D. 这组数据的中位数是36.6
6. 1200000用科学记数法表示为a×10n的形式，则a，n的值是( )
A. a=5，n=5B. a=2，n=−5C. a=5，n=−6D. a=2，n=−6
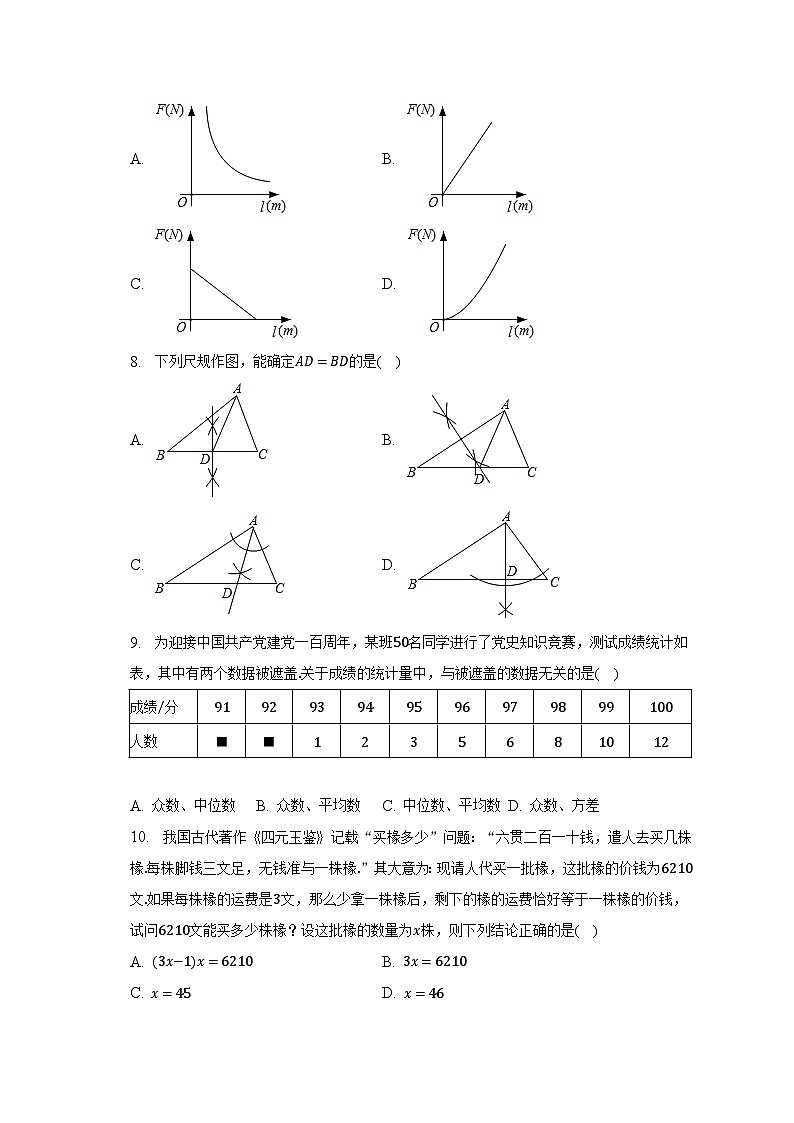
7. 阿基米德说：“给我一个支点，我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识--杠杆原理，即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m，则这一杠杆的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
8. 下列尺规作图，能确定AD=BD的是( )
A. B.
C. D.
9. 为迎接中国共产党建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如表，其中有两个数据被遮盖.关于成绩的统计量中，与被遮盖的数据无关的是( )
A. 众数、中位数B. 众数、平均数C. 中位数、平均数D. 众数、方差
10. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，遣人去买几株椽.每株脚钱三文足，无钱准与一株椽.”其大意为：现请人代买一批椽，这批椽的价钱为6210文.如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为x株，则下列结论正确的是( )
A. (3x−1)x=6210B. 3x=6210
C. x=45D. x=46
11. 如图(1)是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶(拱桥洞的最高点)离水面3m，水面宽6m.如图(2)建立平面直角坐标系，则抛物线的解析式是( )
A. y=−13x2B. y=13x2C. y=−3x2D. y=3x2
12. 如图，将直角三角板ABC放在平面直角坐标系中，点A，B的坐标分别为(2,1)，(6,1).将三角板ABC沿x轴正方向平移，点B的对应点B′刚好落在反比例函数y=10x(x>0)的图象上，则点C平移的距离CC′等于( )
A. 3B. 4C. 7D. 10
13. 如图，将含60°角的直角三角板ABC绕顶点A顺时针旋转45°后得到△AB′C′，点B经过的路径为弧BB′，若∠BAC=60°，AC=3，则图中阴影部分的面积是( )
A. 34πB. 3π2C. 9π2D. 3π
14. 如图，在一张矩形纸片ABCD中，AB=3，BC=9，点E，F分别在AD，BC边
上，将纸片ABCD沿直线EF折叠，点C落在边AD上的一点H处，点D落在点G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时，EF= 10；以上结论中，你认为正确的有个( )
A. 1B. 2C. 3D. 4
二、填空题（本大题共3小题，共10.0分）
15. 有甲、乙、丙三种不同的长方形纸片(边长如图)，现取甲纸片4块，乙纸片1块，丙纸片4块紧密地拼接成一个大正方形(互不重叠)，则大正方形的边长为______ .(用含a的代数式表示)
16. 已知关于x的方程5x−2=3x+16的解与方程4a+1=4(x+a)−5a的解相同，则a=______；若[m]表示不大于m的最大整数，那么[a2−1]=______．
17. 已知二次函数y=(x−2a)2+(a−1)(a为常数)．

(1)若a=1，则二次函数的顶点坐标为______ ；
(2)若抛物线y=(x−2a)2+(a−1)与x轴有一个交点是(2,0)时，则a= ______ ；
(3)当a取不同的值时，其图象构成一个“抛物线系”.如图分别是当a=−1、a=0、a=1、a=2时，二次函数的图象，则它们的顶点坐标满足的函数解析式是______ ．
三、解答题（本大题共7小题，共69.0分。解答应写出文字说明，证明过程或演算步骤）
18. (本小题9.0分)
用直尺画数轴时，数轴上的点A，B，C分别代表数字a，b，c，已知AB=8，BC=3，如图所示，设点p=a+b+c，该轴的原点为O．

(1)若点A所表示的数是−1，则点C所表示的数是______ ；
(2)若点A，B所表示的数互为相反数，则点C所表示的数是______ ，此时p的值为______ ；
(3)若数轴上点C到原点的距离为4，求p的值．
19. (本小题9.0分)
一个三位数，若它的十位数字等于个位数字与百位数字的和，那么称这个三位数为“和谐数”．
(1)最小的三位“和谐数”是______ ，最大的三位“和谐数”是______ ；
(2)若一个“和谐数”的个位数字为a(a≥0)，十位数字为(b≥1,b>a且a、b都是自然数)，请用含a，b的代数式表示该“和谐数”；
(3)判断任意一个三位“和谐数”能否被11整除，若能，请说明理由，若不能，请举出反例．
20. (本小题9.0分)
某校积极落实“双减”政策，将要开设拓展课程，为让学生可以根据自己的兴趣爱好选择最喜欢的课程，进行问卷调查，问卷设置以下四种选项：A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践)，随机抽取了部分学生进行调查，每名学生必须且只能选择其中最喜欢的一种课程，并将调查结果整理绘制成如下不完整的统计图．

根据以上信息，解答下列问题：
(1)此次被调查的学生人数为______ 名，并直接在答题卡中补全条形统计图；
(2)求拓展课程D(劳动实践)所对应的扇形的圆心角的度数；
(3)小明和小兰都从A，B，C，D四种课程中选择一种自己喜欢的课程，请用列表或画树状图的方法求他们选中同一课程的概率．
21. (本小题10.0分)
钓鱼岛及其附属岛屿是中国的固有领土，神圣不可侵犯!自2021年2月1日起，旨在维护国家主权、更好履行海警机构职责的《中华人民共和国海警法》正式实施，中国海警在钓鱼岛海域开展巡航执法活动，是中方依法维护主权的正当举措，如图是钓鱼岛其中一个岛礁，若某测量船在海面上的点D处测得与斜坡AC坡脚点C的距离为150米，测得岛礁顶端A的仰角为30.96°，以及该斜坡AC的坡度i=910，求该岛礁的高(即点A到海平面的铅垂高度).(参考数据：sin30.96°≈0.51，cs30.96°≈0.85，tan30.96°≈0.60)
22. (本小题10.0分)
如图1，点O为矩形ABCD对角线AC的中点，AB=1，AD= 3.沿对角线AC将矩形剪开得到△ADC与△A′BC′，将△A′BC′绕点O逆时针旋转α°(0<α≤120)，记BC′与OC的交点为P，如图2．

(1)①在图2中，连接OB，OD，BD，则△OBD的形状为______ ；
②连接，求证：A′C=BD；
(2)求OP长度的最小值；
(3)当△OPC′的内心在其一边的垂直平分线上时，直接写出α的值．
23. (本小题10.0分)
如图抛物线L1：y=ax2+bx+c经过点A(1,0)和点B(5,0).已知直线L2的解析式为y=kx−5．

(1)如图1，求抛物线L1的解析式；
(2)如图2，若直线L2将线段AB分成1：3两部分，求k的值；
(3)如图3，将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方，将这部分图象与原抛物线剩余的部分组成的新图象记为L3．
①直接写出新图象L3y随x的增大而增大时x的取值范围；
②直接写出直线L2与图象L3有四个交点时k的取值范围．
24. (本小题12.0分)
如图，已知Q是∠BAC的边AC上一点，AQ=10，tan∠BAC=43，点P是射线AB上一点，连接PQ，⊙O经过点A且与QP相切于点P，与边AC相交于另一点D．
(1)PQ的最小值是______ ，当圆心O在射线AB上时，求⊙O的半径：
(2)分别求出AP=4与AP=12时，圆心O到直线AB的距离；
(3)直接写出当⊙O与线段AQ只有一个公共点时，AP的取值范围．
答案和解析
1.【答案】A
【解析】解：∵将△ABC折叠，使点C落在BC边上，
∴AD⊥BC，
∴AD是△ABC的高线，
故选：A．
根据折叠的性质和三角形的高线的定义即可得到结论．
本题考查了翻折变换(折叠问题)，三角形的角平分线、中线和高线，熟练掌握折叠的性质是解题的关键．
2.【答案】D
【解析】解：∵a/​/b，
∴∠4=∠5，
故A正确，不符合题意；
∵a/​/b，
∴∠2+∠3=180°，
故C正确，不符合题意；
∵∠1=∠3，
∴∠1+∠2=180°，
故B正确，不符合题意；
由a/​/b，推不出∠2+∠4=180°，
故D错误，符合题意；
故选：D．
根据平行线的性质定理判断求解即可．
此题考查了平行线的性质，熟记“两直线平行，同位角相等”及“两直线平行，同旁内角互补”是解题的关键．
3.【答案】C
【解析】解：光线由上向下照射正五棱柱时的正投影与俯视图一致．
故选：C．
直接利用正投影的定义得出答案．
此题主要考查了平行投影，正确掌握相关定义是解题关键．
4.【答案】B
【解析】解：A不是中心对称图形，不符合题意；
B是中心对称图形，符合题意；
C不是中心对称图形，不符合题意；
D不是中心对称图形，不符合题意．
故选：B．
根据中心对称图形的定义即可选择．如果一个图形绕某一个点旋转180°后能与它自身重合，我们就把这个图形叫做中心对称图形．
本题考查识别中心对称图形，熟练掌握中心对称图形的定义是解题关键．
5.【答案】D
【解析】解：由折线统计图可以看出这7次的体温数据从第1次到第7次分别为37.1℃、37.0℃、36.5℃、36.6℃、36.8℃、36.8℃、36.7℃．
A、测得的最高体温为37.1℃，故A不符合题意；
B、观察可知，前3次的体温在下降，故B不符合题意；
C、36.8℃出现了2次，次数最高，故众数为36.8℃，故C不符合题意；
D、这七个数据排序为36.5℃，36.6℃，36.7℃，36.8℃，36.8℃，37.0℃，37.1℃.中位数为36.8℃.故D符合题意．
故选：D．
根据统计图和中位数，众数的定义分别进行解答，即可求出答案．
本题考查了折线统计图，主要利用了众数的定义，中位数的定义，根据折线统计图准确获取信息是解题关键．
6.【答案】C
【解析】解：1200000=0.000005=5×10−6．
即a=5，n=−6．
故选：C．
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值<1时，n是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
7.【答案】A
【解析】解：∵阻力×阻力臂=动力×动力臂．小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是1200N和0.5m，
∴动力F(单位：N)关于动力臂l(单位：m)的函数解析式为：1200×0.5=Fl，
则F=600l，是反比例函数，A选项符合，
故选：A．
直接利用阻力×阻力臂=动力×动力臂，进而将已知量据代入得出函数关系式，从而确定其图象即可．
此题主要考查了反比例函数的应用，正确读懂题意得出关系式是解题关键．
8.【答案】B
【解析】解：根据作图方法可得B选项中AD=BD，
故选：B．
要确定AD=BD，首先确定AB的垂直平分线即可．
此题主要考查了作图−基本作图，关键是掌握线段垂直平分线的作法．
9.【答案】A
【解析】解：由表格数据可知，成绩为91分、92分的人数为50−(12+10+8+6+5+3+2+1)=3(人)，
成绩为100分的，出现次数最多，因此成绩的众数是100，
成绩从小到大排列后处在第25、26位的两个数都是98分，因此中位数是98，
因此中位数和众数与被遮盖的数据无关，
故选：A．
通过计算成绩为91、92分的人数，进行判断，不影响成绩出现次数最多的结果，因此不影响众数，同时不影响找第25、26位数据，因此不影响中位数的计算，进而进行选择．
考查中位数、众数、方差、平均数的意义和计算方法，理解各个统计量的实际意义，以及每个统计量所反应数据的特征，是正确判断的前提．
10.【答案】D
【解析】解：根据题意得：3x(x−1)=6210，
整理得：x2−x−2070=0，
解得：x1=46，x2=−45(不符合题意，舍去)．
即这批椽的数量为46株．
故选：D．
根据少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，列出一元二次方程，解方程即可．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
11.【答案】A
【解析】解：设出抛物线方程y=ax2(a≠0)，
由图象可知该图象经过(−3,−3)点，
故−3=9a，
a=−13，
故y=−13x2，
故选：A．
设出抛物线方程y=ax2(a≠0)代入坐标求得a．
本题主要考查二次函数的应用，解题的关键是熟练掌握待定系数法求函数解析式．
12.【答案】B
【解析】解：∵点A，B的坐标分别为(2,1)，(6,1).将三角板ABC沿x轴正方向平移，
∴点B′的纵坐标为1，BB′=CC′，
当y=1时，10x=1，解得x=10，
∴B′(10,1)，
∴BB′=10−6=4，
∴CC′=4．
故选：B．
先根据平移的性质得到点B′的纵坐标为1，BB′=CC′，则利用反比例函数解析式可确定B′(10,1)，则BB′=4，从而得到CC′的长度．
本题考查了反比例函数图象上点的坐标特征：反比例函数y=kx(k为常数，k≠0)的图象是双曲线，图象上的点(x,y)的横纵坐标的积是定值k，即xy=k.也考查了平移的性质．
13.【答案】C
【解析】解：在Rt△ABC中，∠ACB=90°，∠BAC=60°，AC=3，
∴∠ABC=30°．
∴AB=2AC=6．
根据旋转的性质知△ABC≌△AB′C′，则S△ABC=S△AB′C′，AB=AB′．
∴S阴影=S扇形ABB′+S△AB′C′−S△ABC
=45π×62360
=9π2．
故选：C．
图中S阴影=S扇形ABB′+S△AB′C′−S△ABC．
本题考查了扇形面积的计算、旋转的性质．求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．
14.【答案】B
【解析】解：①∵HE//CF，
∴∠HEF=∠EFC，
∵将纸片ABCD沿直线EF折叠，点C落在边AD上的一点H处，
∴∠EFC=∠HFE，FC=HF，EC=HE，
∴∠HEF=∠HFE，
∴HE=HF，
∴FC=HF=HE=EC，
∴四边形CFHE是菱形，故①正确；
②∴∠BCH=∠ECH，
∴只有∠DCE=30°时EC平分∠DCH，故②错误；
③若点H与点A重合时，如图：

设BF=x，则AF=FC=9−x，
在Rt△ABF中，AB2+BF2=AF2，
∴32+x2=(9−x)2，
解得x=4，
若点E与点D重合时，CF=CD=3，
∴BF=6，
∴线段BF的取值范围为4≤BF≤6，故③错误；
④当点H与点A重合时，过点F作FM⊥AD于M，

∵BF=4，
∴CF=BC−BF=5=AE=AF，
∴ME=AE−AM=AE−BF=5−4=1，
由勾股定理得，
EF= ME2+MF2= 12+32= 10，故④正确；
综上所述，结论正确的有①④共2个．
故选：B．
①由矩形性质和翻折的性质，可证明四边形CFHE是菱形，判断出①正确；
②根据菱形的对角线平分一组对角线可得∠BCH=∠ECH，然后求出只有∠DCE=30°时EC平分∠DCH，判断出②错误；
③点H与点A重合时，设BF=x，表示出AF=FC=9−x，利用勾股定理列出方程求解得到BF的最小值，点G与点D重合时，CF=CD，求出BF=6，判断③错误；
④过点F作FM⊥AD于M，求出ME，再利用勾股定理列式求解得到EF，判断出④正确．
此题是四边形综合题，主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用，熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键．
15.【答案】2a+5
【解析】解：∵甲纸片4块，乙纸片1块，丙纸片4块，
∴大正方形的面积=4a2+25+4×5a=(2a+5)2，
∴大正方形的边长为2a+5．
故答案为：2a+5．
先求出大正方形的面积，再求出其边长即可．
本题考查的是完全平方公式，根据题意得出大正方形的面积是解题的关键．
16.【答案】7 2
【解析】解：解方程5x−2=3x+16，得x=9，
将x=9代入4a+1=4(x+a)−5a，
得a=7，
所以[72−1]=2．
故答案为：7；2．
先解方程5x−2=3x+16，得x=9，将x=9代入4a+1=4(x+a)−5a，求出a的值，代入a的值进而可得结果．
本题考查了同解方程，本题的关键是正确解一元一次方程．理解方程的解的定义，就是能够使方程左右两边相等的未知数的值．
17.【答案】(2,0) 1或34 y=12x−1．
【解析】解：(1)∵二次函数y=(x−2a)2+(a−1)的顶点坐标为(2a,a−1)，
∴当a=1时，2a=2，a−1=0，
∴这个二次函数的顶点坐标为(2,0)；
故答案为：(2,0)．
(2)将点(2,0)代入y=(x−2a)2+(a−1)，得：0=(2−2a)2+(a−1)，
解得：a1=1，a2=34，
∴当a=1时，抛物线y=(x−2a)2+(a−1)与x轴只有一个交点(2,0)；
当a=34时，抛物线y=(x−2a)2+(a−1)与x轴有两个个交点，其中一个是(2,0)，
∴抛物线y=(x−2a)2+(a−1)与x轴有一个交点是(2,0)时，则a=1或34；
故答案为：1或34．
(3)对于二次函数y=(x−2a)2+(a−1)，顶点横坐标x=2a，顶点的纵坐标y=a+1，
由y=a+1得：a=y−1，
∴x=2(y−1)，
∴y=12x−1，
∴顶点坐标所满足的函数解析式为：y=12x−1．
故答案为：y=12x−1．
(1)首先求出二次函数y=(x−2a)2+(a−1)的顶点坐标为(2a,a−1)，然后根据a=1可求出这个二次函数的顶点坐标；
(2)将点(2,0)代入y=(x−2a)2+(a−1)之中即可求出a的值；
(3)对于二次函数y=(x−2a)2+(a−1)，顶点横坐标x=2a，纵坐标y=a+1，然后由y=a+1得a=y−1，由此得x=2(y−1)，据此了得出答案．
此题主要考查了二次函数的图象，解答此题的关键是熟练掌握二次函数的顶点坐标，与x轴的交点，难点是解答(3)时，根据顶点的横坐标x=2a，顶点的纵坐标y=a+1，而得出x与y的函数关系式．
18.【答案】10 7 7
【解析】解：(1)∵AB=8，BC=3，
∴AC=AB+BC=8+3=11，
∵点A所表示的数是−1，
∴点C所表示的数是−1+11=10；
故答案为：10．
(2)∵点A，B所表示的数互为相反数，
∴原点O是线段AB的中点，
∵AB=8，
∴OA=OB=4，
∴a=−4，b=4，
∵BC=3，
∴c=3+4=7，
p=a+b+c=−4+4+7=7，
故答案为：7，7．
(3)∵点C表示的数为4，AB=8，BC=3，
∴c=4时，b=4−3=1，a=1−8=−7，
c=−4时，b=−4−3=−7，a=−7−8=−15，
∴p=a+b+c=−7+1+4=−2，或p=−15−7−4=−26．
(1)根据数轴上两点间的距离与两点表示的实数间的关系计算即可；
(2)根据相反数和线段的中点的定义，运用有理数的加、减法则计算即可；
(3)根据数轴上两点间的距离与两点表示的实数间的关系，以及有理数的加、减法则计算即可．
本题考查数轴上两点距离、相反数的概念，涉及线段的中点，线段的和差计算，有理数的加减运算等知识．
19.【答案】110 990
【解析】解：(1)设个位数字为x(x≥0)，百位数字为y(y>0)，则十位数字为x+y，
∴“和谐数”为：100y+10(x+y)+x=110y+11x，
当x=0，y=1时，有最小的三位“和谐数”是110，
当x=0，y=9时，有最大的三位“和谐数”是990，
故答案为：110，990；
(2)100(b−a)+10b+a=100b−100a+10b+a=110b−99a，
∴该“和谐数”为：110b−99a；
(3)能，理由：
由(1)得“和谐数”为：100y+10(x+y)+x=110y+11x，
∵110y+11x=11(10y+x)，
∴任意一个三位“和谐数”能被11整除．
(1)设个位数字为x(x≥0)，百位数字为y(y>0)，则十位数字为x+y，则“和谐数”为：100y+10(x+y)+x=110y+11x，由此可得结论；
(2)按题意列代数式即可；
(3)由110y+11x=11(10y+x)可得结论．
本题属于新定义问题，涉及到列代数式、整式加减等问题，正确理解新定义是解决本题的关键．
20.【答案】120
【解析】解：(1)此次被调查的学生人数为12÷10%=120(名)；
B的人数为：120−12−48−24=36(名)，
补图如下：
；
(2)拓展课程D(劳动实践)所对应的扇形的圆心角的度数为360°×24120=72°；
(3)
共有16种等可能结果，选中同一课程有4种；
他们选中同一课程的概率为：416=14．
(1)利用A的人数除以A的百分比即可；利用总人数乘以B的百分比求出B的人数，然后完成统计图即可；
(2)利用360×D的百分比即可；
(3)列树状图判断即可．
本题考查扇形统计图、条形统计图，明确题意，从统计图中获取解答问题的信息是解答本题的关键．
21.【答案】解：∵斜坡AC的坡度i=910，
∴AB：BC=10：9，
故可设AB=10x米，BC=9x米，
在Rt△ADB中，∠D=30.96°，BD=(150+10x)米，
∴tan30.96°=9x150+10x=0.60，
解得：x=30，
经检验，x=30是方程的解，
∴9x=270(米)，
答：该岛礁的高AB为270米．
【解析】根据斜坡AC的坡度i=56，可设AB=5x米，BC=6x米，继而表示出BD的长度，再由tan30.96°≈0.60，可得关于x的方程，解出即可得出答案．
本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形，利用三角函数的定义，表示相关线段的长度．
22.【答案】等腰三角形
【解析】(1)①解：如图1，∵AB=CD=1，AD=BC= 3，
∴AC= AB2+BC2= 1+3=2，
∴sin∠ACB=ABAC=12，
∴∠ACB=30°，
如图2，

∵将△A′BC′绕点O逆时针旋转α°(0<α≤120)，
∴AC=A′C′，A′B=1，
∵∠ADC=90°，点O是AC的中点，
∴DO=CO=12AC=1，
∵∠A′BC′=90°，点O是A′C′的中点，
∴OB=C′O=A′O=12A′C′=1，
∴OB=OD=1，
∴△BOD是等腰三角形；
故答案为：等腰三角形；
②证明：∵A′O=BO=A′B=1，
∴△A′OB是等边三角形，
∴∠A′OB=60°，
同理可证：∠COD=60°，
∴∠A′OB=∠COD，
∴∠A′OC=∠BOD，
又∵A′O=CO=BO=DO=1，
∴△A′OC≌△BOD(SAS)，
∴A′C=BD；
(2)∵点P在BC′上移动，
∴当OP⊥BC′时，OP有最小值，
∵∠A′C′B=30°，OP⊥BC′，
∴OP=12OC′=12，
∴OP的最小值为12；
(3)∵△OPC′的内心在其一边的垂直平分线上，
∴△OPC′是等腰三角形，
当OP=C′P时，则∠POC′=∠C′=30°，
∴α=30，
当OC′=C′P时，则∠POC′=180°−30°2=75°，
∴α=75，
当OC′=OP时，则∠OPC′=∠OC′P=30°，
∴∠POC′=120°，
∴α=120，
综上所述：α的值为30或75或120．
(1)①由旋转的性质可得AC=A′C′，A′B=2，由直角三角形的性质，可得BO=DO=2，即可求解；
②由“SAS”可证△A′OC≌△BOD，可得A′C=BD；
(2)由垂线段最短可得当OP⊥BC′时，OP有最小值，由直角三角形的性质可求解；
(3)分三种情况讨论，由等腰三角形的性质可求解．
本题是四边形综合题，考查了全等三角形的判定和性质，矩形的性质，等腰三角形的性质，旋转的性质等知识，利用分类讨论思想解决问题是解题的关键．
23.【答案】解：(1)∵直线L2的解析式为y=kx−5，
∴M(0,−5)，
∵y=ax2+bx+c经过点A(1,0)和点B(5,0)，
∴ c=−5a+b+c=025a+5b+c=0，
∴a=−1b=6c=−5，
∴抛物线L1的解析式为y=−x2+6x−5；
(2)设直线L2与x轴的交点为C，
∵点A(1,0)和点B(5,0)，
∴AB=4，
∵直线L2将线段AB分成1：3两部分，
∴AC=1或AC=3，
∴C(2,0)或(4,0)，代入y=kx−5得k=52或54；
(3)①y=−x2+6x−5的对称轴是直线x=3，点A(1,0)和点B(5,0)，
当x≤1或3≤x≤5时新图象L3y随x的增大而增大；
②如图所示，当直线y=kx−5夹在两条虚线之间时直线L2与图象L3有四个交点，把B(5,0)代入y=kx−5得k=1；
∵y=−x2+6x−5的顶点是(3,4)，
∴将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方后，顶点变为(3,−4)，
∴折叠后的抛物线表达式为y=(x−3)2−4=x2−6x+5，
联立y=kx−5和y=x2−6x+5得y=kx−5y=x2−6x+5，
∴x2−6x+5=kx−5，即x2−(6+k)x+10=0，
∴Δ=(6+k)2−40=0，
∴k=2 10−6或k=−2 10−6，
∵k>0，
∴k=2 10−6，
∴2 10−6
【解析】(1)先求M点再利用待定系数法求抛物线L1的解析式；
(2)先确定分点的坐标，代入直线L2的解析式求k的值；
(3)①观察图象上升的部分对应x的范围；
②直线y=kx−5过(0,−5)，利用数形结合观察有四个交点的情形，求出临界值，再写k的范围．
本题考查了一次函数和二次函数的图象与性质，结合了对称变换，渗透了数形结合的思想，对于(3)②，关键是找到并求出k的临界值．
24.【答案】8
【解析】解：(1)如图1，

当PQ⊥AB时，PQ最小，
∴tan∠BAC=PQAP=43，
设PQ=4k，AP=3k，
∴(4k)2+(3k)2=102，
∴k1=2，k2=−2(舍去)，
∴PQ=8，AP=6，
∵点O在AB上，
∴AP是⊙O的直径，
∴⊙O的半径为：3，
故答案为：8；
(2)如图2，

当AP=4时，连接PO，作OT⊥AB于T，作QR⊥AB于R，
∴AT=PT=12AP=2，∠OTP=∠PRQ=90°，
∴∠TOP+∠OPT=90°，
∵PQ是⊙O的切线，
∴OP⊥PQ，
∴∠OPQ=90°，
∴∠OPT+∠RPQ=90°，
∴∠TOP=∠RPQ，
∴△POT∽△QRP，
∴OTPR=PTQR，
∴OT2=28，
∴OT=12，
∴O到直线AB的距离为：12，
如图3，

当AP=12时，作QR⊥AP于R，连接OP，
∵AR=6，
∴QR经过圆心O，
由上知：∠OPQ=90°，
∴∠QPR+∠OPR=90°，∠O+∠OPR=90°，
∴∠QPR=∠O，
∵∠QRP=∠PRO=90°，
∴△QPR∽△POR，
∴PRQR=ORPR，
∴68=OR6，
∴OR=92，
∴圆心O到AB距离为：92；
(3)由(2)知：当AP=12时，⊙O与线段AQ只有一个公共点，
∴AP≥12．
(1)当PQ⊥AB时，PQ最小，由tan∠BAC=PQAP=43设PQ=4k，AP=3k，从而(4k)2+(3k)2=102，求得k=2，进一步得出结果；
(2)当AP=4时，连接PO，作OT⊥AB于T，作QR⊥AB于R，可证得△POT∽△QRP，从而OTPR=PTQR，从而OT2=28，进一步得出结果；当AP=12时，作QR⊥AP于R，连接OP，可证得△QPR∽△POR，从而PRQR=ORPR，从而68=OR6，进一步得出结果；
(3)在(2)的临界情况下，进一步得出结果．
本题考查了圆的切线性质，相似三角形的判定和性质，锐角三角函数的定义等知识，解决问题的关键是熟练运用相似三角形知识．
成绩/分
91
92
93
94
95
96
97
98
99
100
人数
■
■
1
2
3
5
6
8
10
12