2022-2023学年重庆市渝北区六校联考七年级（下）第一次月考数学试卷（含解析）

这是一份2022-2023学年重庆市渝北区六校联考七年级（下）第一次月考数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年重庆市渝北区六校联考七年级（下）第一次月考数学试卷
一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）
1. 3排5号用有序数对(3,5)表示，则4排2号可以表示为(    )
A. (4,2) B. (2,4) C. (4,4) D. (2,2)
2. 在实数−23，0， 6，−π， 4，327中，无理数有(    )
A. 1个 B. 2个 C. 3个 D. 4个
3. 点A(−3,3)与点B(−3,−1)两点之间的距离为(    )
A. 1 B. 2 C. 3 D. 4
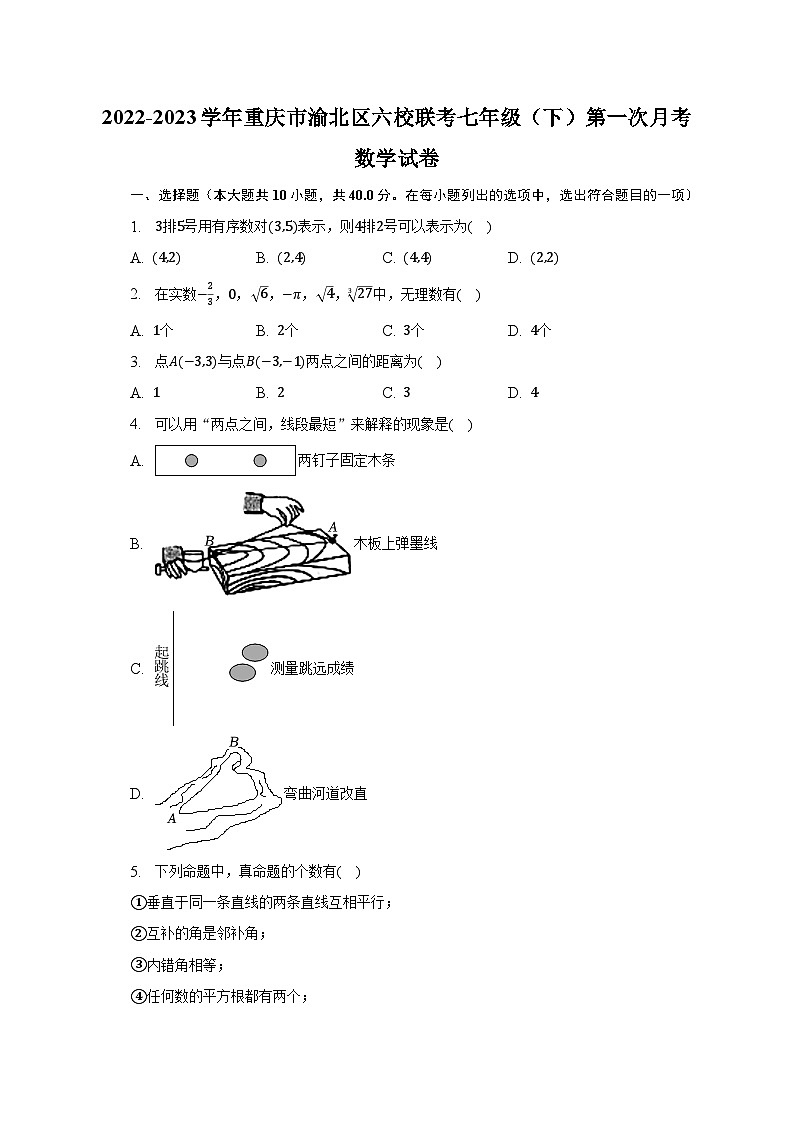
4. 可以用“两点之间，线段最短”来解释的现象是(    )
A. 两钉子固定木条
B. 木板上弹墨线
C. 测量跳远成绩
D. 弯曲河道改直
5. 下列命题中，真命题的个数有(    )
①垂直于同一条直线的两条直线互相平行；
②互补的角是邻补角；
③内错角相等；
④任何数的平方根都有两个；
⑤平移前后图形的形状和大小都没有发生改变；
⑥负数没有立方根．
A. 1个 B. 2个 C. 3个 D. 4个
6. 已知，如图，AB//CD，将一副三角尺如图摆放，让一个顶点和一条边分别放在AB和CD上，则∠AEF=(    )

A. 10° B. 12° C. 15° D. 18°
7. 如图，输入m=2 2，则输出的数为(    )


A. 8 B. 16 C. 32 D. 64
8. a−b−3+|2a−4|=0，则a+b=(    )
A. a+b=−1 B. a+b=1 C. a+b=2 D. a+b=3
9. 若[x]表示不小于x的最小整数，如[−1]=−1，[1.5]=2；{x}表示按四名五入法精确到个位所取的近似数，如{5.67}=6，{2.34}=2；若a=[π]，b={π}，则a，b两个数的大小关系为(    )
A. ab D. 不确定
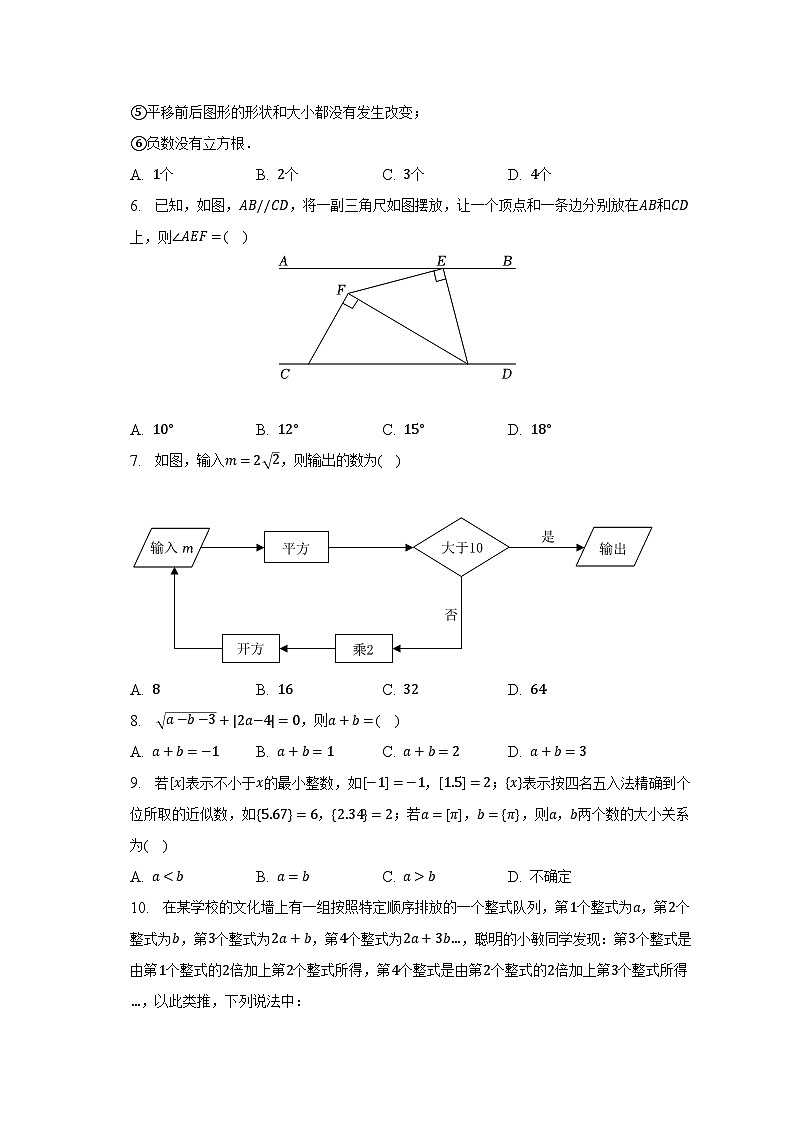
10. 在某学校的文化墙上有一组按照特定顺序排放的一个整式队列，第1个整式为a，第2个整式为b，第3个整式为2a+b，第4个整式为2a+3b…，聪明的小敏同学发现：第3个整式是由第1个整式的2倍加上第2个整式所得，第4个整式是由第2个整式的2倍加上第3个整式所得…，以此类推，下列说法中：
①第8个整式为42a+43b；
②第2025个整式中a的系数比b的系数小1；
③第12个整式和第13个整式中a的所有系数与b的所有系数之和为4098；
④若将第2n个整式与第2n+1个整式相加，所得的多项式中a的系数与b的系数相等(其中n为正整数)；
正确的有个．(    )
A. 1 B. 2 C. 3 D. 4
二、填空题（本大题共8小题，共32.0分）
11. 16的平方根是______ ．
12. 如果x、y分别是4− 3的整数部分和小数部分，则x−y= ______ ．
13. 已知点A(−1,b+2)在x轴上，则b= ______ ．
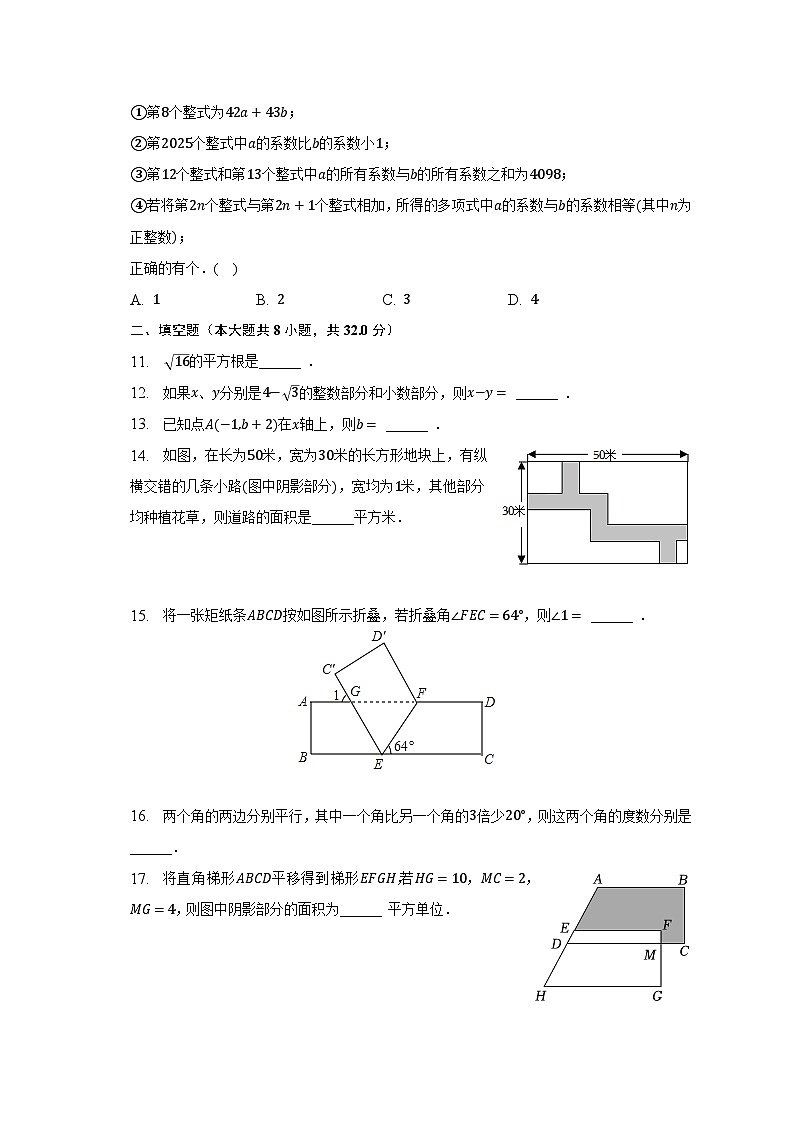
14. 如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路(图中阴影部分)，宽均为1米，其他部分均种植花草，则道路的面积是______平方米．


15. 将一张矩纸条ABCD按如图所示折叠，若折叠角∠FEC=64°，则∠1= ______ ．

16. 两个角的两边分别平行，其中一个角比另一个角的3倍少20°，则这两个角的度数分别是______．
17. 将直角梯形ABCD平移得到梯形EFGH，若HG=10，MC=2，MG=4，则图中阴影部分的面积为______ 平方单位．


18. 如图，数轴上有A、B两点，O是坐标原点，A、B所表示的有理数分别为a、b，且a、b满足(a+24)2=−|b−12|.若动点P从A出发，以每秒3个单位长度的速度沿数轴向右运动；点Q从B出发，以每秒2个单位长度的速度沿数轴向左运动，当点P运动到点B时P、Q两点同时停止运动，设运动时间为t，当t= ______ 秒时，2OP−OQ=8．
三、解答题（本大题共8小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题8.0分)
(1)计算：(−3)2+327；
(2)求3(x−1)2−75=0中x的值．
20. (本小题10.0分)
完成下列推理过程：
已知：如图，∠1+∠2=180°，∠3=∠B，
求证：∠EDG+∠DGC=180°．
证明：∵∠1+∠2=180°(已知)，
又∵∠1+∠DFE=180° (______ )，
∴∠2=∠DFE(______ ).
∴EF//AB (______ ).
∴ ______ = ______ (______ ).
又∵∠3=∠B (______ )，
∴∠B=∠ADE (______ ).
∴DE//BC (______ ).
∴∠EDG+∠DGC=180° (______ ).

21. (本小题10.0分)
如图，平面直角坐标系中，已知点A(−3,3)，B(−5,1)，C(−2,0)，P(a,b)是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1，点P的对应点为P1(a+6,b−2 )．
(1)直接写出点A1，B1，C1的坐标；
(2)在图中画出△A1B1C1；
(3)连接AA1，求△AOA1的面积．





22. (本小题10.0分)
如图，OA⊥OB，射线OC在∠AOB内部，射线OD在∠AOB外部，且∠AOC=2∠BOC，∠COD=60°．
(1)求∠BOC的度数：
(2)求证：OC平分∠AOD．

23. (本小题10.0分)
(1)已知一个正数的两个不同平方根分别是a+3与2a−15，求这个数．
(2)已知x，y为实数，且y= x−9− 9−x+4，求 xy的平方根．
24. (本小题10.0分)
已知在平面直角坐标中，A(−2,3)，B(4,3)，C(−1,−3).(请画出图形)，完成下列问题：
(1)直接写出点C到x轴的距离；
(2)求A、B之间的距离；
(3)点P为y轴上一点，当S△ABP=13S△ABC时，求点P的坐标．
25. (本小题10.0分)
甲、乙两工程队共同承包了一段长4600米的排污管道铺设工程，计划由两工程队分别从两端相向施工.已知甲队平均每天可完成230米，乙队平均每天比甲队多完成115米．
(1)若甲乙两队同时施工，共同完成全部任务需要几天？
(2)若甲乙两队共同施工5天后，甲队被调离去支援其他工程，剩余的部分由乙队单独完成，则乙队需再施工多少天才能完成任务？
26. (本小题10.0分)
如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．
(1)试判断直线AB与直线CD的位置关系，并说明理由；
(2)如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF//GH；
(3)如图3，在(2)的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请直接写出其值．
答案和解析

1.【答案】A 
【解析】解：3排5号用有序数对(3,5)表示，
则4排2号可以表示为(4,2)．
故选：A．
根据有序数对的表示方法即可获得答案．
本题主要考查的是坐标确定位置，理解并掌握有序数对概念是解题关键．

2.【答案】B 
【解析】解：∵ 4=2,327=3，
∴无理数的有 6，−π共2个．
故选：B．
根据无理数的概念及立方根、算术平方根可进行求解．
本题主要考查无理数、算术平方根及立方根，熟练掌握无理数的概念是解题的关键．

3.【答案】D 
【解析】解：∵点A(−3,3)与点B(−3,−1)的横坐标都是−3，
∴只求出纵坐标对应点的距离即可，
∴AB=|3−(−1)|=4，
故选：D．
根据题意得到AB=|3−(−1)|，于是得到结论．
本题考查了坐标系中两点之间的距离，本题比较简单．

4.【答案】D 
【解析】解：AB的数学常识均为两点确定一条直线，
C的数学常识为垂线段最短，
D的数学常识为两点之间，线段最短．
故选：D．
用两根钉子就可以把一根木条固定在墙上是两点确定一条直线；木板上弹墨线，能弹出一条笔直的墨线，而且只能弹出一条墨线，可用两点确定一条直线来解释的现象；测量跳远成绩是垂线段最短求脚后跟到起跳线的距离；把弯曲的河道改直，就能够缩短路程是两点之间，线段最短；据此分别判断即可．
本题考查了数学常识在生活中的应用，熟练掌握数学常识是解题的关键．

5.【答案】A 
【解析】解：①平面内，垂直于同一条直线的两条直线互相平行，故原命题错误，是假命题，不符合题意；
②互补的角不一定是邻补角，故原命题错误，是假命题，不符合题意；
③两直线平行，内错角相等，故原命题错误，是假命题，不符合题意；
④任何正数的平方根都有两个，故原命题错误，是假命题，不符合题意；
⑤平移前后图形的形状和大小都没有发生改变，正确，是真命题，符合题意；
⑥负数有立方根，故原命题错误，是假命题，不符合题意，
真命题有1个，
故选：A．
利用平行线的性质、邻补角的定义、平行线的性质及平移的性质等知识分别判断后即可确定正确的选项．
考查了命题与定理的知识，解题的关键是了解平行线的性质、邻补角的定义、平行线的性质及平移的性质等知识，难度不大．

6.【答案】C 
【解析】解：如图所示，过点F作FG//AB，

∵AB//CD，
∴FG//AB//CD，
∵∠FCD=60°，
∴∠CFG=180°−∠FCD=120°，
∵∠CFD=90°，
∴∠GFD=∠CFG−∠DFC=120°−90°=30°，
∵∠EFD=45°，
∴∠EFG=∠EFD−∠GFD=45°−30°=15°，
∵FG//AB，
∴∠AEF=∠EFG=15°．
故选：C．
过点F作FG//AB，根据平行线的性质得出∠CFG=120°，进而得出∠GFD=30°，∠EFG=15°，根据FG//AG，即可求解．
本题考查三角形内角和定理及平行线的性质与判定，数形结合是解题的关键．

7.【答案】B 
【解析】解：∵m=2 2时，m2=(2 2)2=8<10，
∴ 2×8=4，再输入4，
42=16>10，
∴输出的数是16．
故选：B．
把m=2 2代入程序进行计算即可．
本题考查的是算术平方根，根据题意弄懂输入程序是解题的关键．

8.【答案】B 
【解析】解：∵ a−b−3+|2a−4|=0， a−b−3≥0,|2a−4|≥0，
∴ a−b−3=0,|2a−4|=0，
∴a−b−3=0，2a−4=0，
解得：a=2，b=−1，
∴a+b=1．
故选：B．
根据算术平方根和绝对值的非负性，可得a−b−3=0，2a−4=0，从而得到a=2，b=−1，即可求解．
本题主要考查了算术平方根和绝对值的非负性，熟练掌握算术平方根和绝对值的非负性是解题的关键．

9.【答案】B 
【解析】解：∵[x]表示不小于x的最小整数，{x}表示按四名五入法精确到个位所取的近似数，a=[π]，b={π}，π≈3.14，
∴a=3，b=3，
∴a=b．
故选：B．
先根据题意求出a，b的值，再比较其大小即可．
本题考查的是有理数的大小比较，熟知π≈3.14是解题的关键．

10.【答案】B 
【解析】解：根据题意得：第1个整式为a，
第2个整式为b，
第3个整式为2a+b，
第4为2a+3b，
第5个整式为2a+3b+2(2a+b)=6a+5b，
第6个整式为6a+5b+2(2a+3b)=10a+11b，
第7个整式为10a+11b+2(6a+5b)=22a+21b，
第8个整式为22a+21b+2(10a+11b)=42a+43b，故①正确；
……
由此发现，第奇数个整式中a的系数比b的系数大1，第偶数个整式中a的系数比b的系数小1，
∴将第2n个整式与第2n+1个整式相加，所得的多项式中a的系数与b的系数相等，故④正确；
∴第2025个整式中a的系数比b的系数大1，故②错误；
根据题意得：第2个整式和第3个整式中a的所有系数与b的所有系数之和为4=22；
第4个整式和第5个整式中a的所有系数与b的所有系数之和为16=24；
第6个整式和第7个整式中a的所有系数与b的所有系数之和为64=26；
……
第12个整式和第13个整式中a的所有系数与b的所有系数之和为212=4096，故③错误；
故选：B．
根据写出前8个整式，可得第奇数个整式中a的系数比b的系数大1，第偶数个整式中a的系数比b的系数小1；根据题意得：第2个整式和第3个整式中a的所有系数与b的所有系数之和为4=22；第4个整式和第5个整式中a的所有系数与b的所有系数之和为16=24；第6个整式和第7个整式中a的所有系数与b的所有系数之和为64=26，……由此可得第12个整式和第13个整式中a的所有系数与b的所有系数之和为4098，即可求解．
本题考查数字的变化规律，通过计算，探索出整式各项系数之间的关系，找到系数和的规律是解题的关键．

11.【答案】±2 
【解析】解：∵ 16=4，(±2)2=4，
∴4的平方根是±2，
∴ 16的平方根是±2．
故答案为：±2．
16的值为4，求4的平方根即可．
本题考查数的平方根，正确记忆平方根的定义是解题关键．

12.【答案】 3 
【解析】解：∵1<3<4，
∴1< 3<2，
∴−1>− 3>−2，
∴3>4− 3>2．
∴x=2，y=4− 3−2=2− 3．
∴x−y=2−(2− 3)= 3．
故答案为： 3．
先估算出 3的大小，然后利用不等式的性质得到4− 3的范围，从而得到x、y的值，然后代入计算即可．
本题主要考查的是估算无理数的大小，利用不等式的性质确定出4− 3的范围是解题的关键．

13.【答案】−2 
【解析】解：由点A(−1,b+2)在x轴上，得
b+2=0．
解得b=−2，
故答案为：−2．
根据x轴上的点的纵坐标为零，可得方程，根据解方程，可得答案．
本题考查了点的坐标，利用x轴上点的纵坐标为零得出方程是解题关键．

14.【答案】79 
【解析】解：根据题可知，可以根据平移的性质，把小路相当于一条横向长为50米与一条纵向长为30米的小路，
∴小路的面积为30×1+50×1−1×1=79(平方米)，
故答案为：79．
根据题可知，可以根据平移的性质，把小路相当于一条横向长为50米与一条纵向长为30米的小路，再利用长方形的面积公式计算小路的面积即可．
本题考查了图形的平移的性质，把小路进行平移，求出相当面积的小路的面积是解题的关键．

15.【答案】52° 
【解析】解：∵∠GEF=∠FEC=64°，
∴∠BEG=180°−64°×2=52°，
∵AD//BC，
∴∠1=∠BEG=52°．
故答案为：52°．
根据翻折变换的性质求出∠GEF的度数，从而求出∠GEB的度数，再根据平行线的性质求出∠1的度数．
本题考查的是图形翻折变换的性质及等腰三角形的判定定理，熟知图形翻折不变性的性质是解答此题的关键．

16.【答案】10°，10°或130°，50° 
【解析】解：∵两个角的两边都平行，
∴此两角互补或相等，
设其中一个角为x°，
∵其中一个角的度数是另一个角的3倍少20°，
∴若两角相等，则x=3x−20，解得：x=10，
∴若两角互补，则x=3(180−x)−20，解得：x=130，
两个角的度数分别是10°，10°或130°，50°．
故答案为：10°，10°或130°，50°．
由两个角的两边都平行，可得此两角互补或相等，然后设其中一个角为x°，分别从两角相等或互补去分析，由其中一个角的度数是另一个角的3倍少20°，列方程求解即可求得答案．
此题考查了平行线的性质．此题难度不大，解题的关键是掌握若两个角的两边都平行，则此两角互补或相等，注意方程思想的应用．

17.【答案】36 
【解析】解：根据平移的性质得S梯形ABCD=S梯形EFGH，
∵DC=HG=10，MC=2，MG=4，
∴DM=DC−MC=10−2=8，
∴S阴影=S梯形ABCD−S梯形EFMD
=S梯形EFGH−S梯形EFMD
=S梯形HGMD
=12(DM+HG)⋅MG
=12×(8+10)×4
=36．
故答案为：36．
根据图形可知图中阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积，恰好等于梯形EFGH的面积减去梯形EFMD的面积．
主要考查了梯形的性质和平移的性质，要注意平移前后图形的形状和大小不变，本题的关键是能得到：图中阴影部分的面积等于梯形ABCD的面积减去梯形EFMD的面积，恰好等于梯形EFGH的面积减去梯形EFMD的面积．

18.【答案】6.5或11 
【解析】解：∵(a+24)2=−|b−12|，
∴(a+24)2+|b−12|=0，
∵(a+24)2≥0，|b−12|≥0，
∴a+24=0，b−12=0，
∴a=−24，b=12，
∴A、B所表示的有理数分别为−24、12，
∴OA=24，OB=12，
在点Q运动到原点之前，即0≤t≤6时，
此时OP=24−3t，OQ=12−2t，
由2OP−OQ=8得到，2(24−3t)−(12−2t)=8，
解得t=7(不合题意，舍去)；
在点Q运动经过原点，但点P没到原点，即6 此时OP=24−3t，OQ=2t−12，
由2OP−OQ=8得到，2(24−3t)−(2t−12)=8，
解得t=6.5，符合题意；
在点Q运动经过原点，点P也经过原点后，即8 此时OP=3t−24，OQ=2t−12，
由2OP−OQ=8得到，2(3t−24)−(2t−12)=8，
解得t=11，符合题意；
综上可知，当t=6.5或11秒时，2OP−OQ=8．
故答案为：6.5或11．
根据(a+24)2=−|b−12|求出a=−24，b=12，得到A、B所表示的有理数分别为−24、12，则OA=24，OB=12，分在点Q运动到原点之前；点Q运动经过原点，但点P没到原点；点Q运动经过原点，点P也经过原点后三种情况，分别列方程求解即可．
此题主要考查了一元一次方程的应用，还考查了非负数的性质，读懂题意，分情况讨论是解题的关键．

19.【答案】解：(1)原式=9+3=12，
(2)3(x−1)2−75=0，
(x−1)2=25，
∴x−1=5或x−1=−5，
解得：x1=6，x2=−4． 
【解析】(1)根据实数运算法则运算即可；
(2)用直接开平方法计算即可．
本题考查了一元二次方程的解法，直接开平方法．

20.【答案】邻补角定义  同角的补角相等  内错角相等，两直线平行  ∠3  ∠ADE  两直线平行，内错角相等  已知  等量代换  同位角相等，两直线平行  两直线平行，同旁内角互补 
【解析】证明：∵∠1+∠2=180°(已知)，

又∵∠1+∠DFE=180°(邻补角定义)，
∴∠2=∠DFE(同角的补角相等)，
∴EF//AB(内错角相等，两直线平行)，
∴∠3=∠ADE(两直线平行，内错角相等)，
∵∠3=∠B(已知)，
∴∠B=∠ADE(等量代换)，
∴DE//BC(同位角相等，两直线平行)，
∴∠EDG+∠DGC=180°(两直线平行，同旁内角互补)．
故答案为：邻补角定义；同角的补角相等；内错角相等，两直线平行；∠；∠ADE；两直线平行，内错角相等；已知；等量代换；同位角相等，两直线平行；两直线平行，同旁内角互补．
根据同角的补角相等可证明∠2=∠DFE，进而可证EF//AB，再证明∠B=∠ADE，可证DE//BC，进而可证结论成立．
本题考查了平行线的性质与判定，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．

21.【答案】解：(1)A1(3,1)，B1(1,−1)，C1(4,−2)；
(2)△A1B1C1如图所示；

(3)如图，连接OA，OA1，AA1，
△AOA1的面积=6×3−12×3×3−12×3×1−12×6×2
=18−92−32−6，
=6． 
【解析】
【分析】
(1)根据点P，P1的坐标确定出平移规律为向右平移6个单位，再向下平移2个单位，再求出点A1，B1，C1的坐标即可；
(2)根据网格结构找出点A，B，C平移后的对应点A1，B1，C1的位置，然后顺次连接即可；
(3)利用△AOA1所在的长方形的面积减去四周三个小直角三角形的面积，列式计算即可得解．
【解答】
解：(1)由P(a,b)及其对应点P1(a+6,b−2 )可知平移规律为向右平移6个单位，再向下平移2个单位，
∵A(−3,3)，B(−5,1)，C(−2,0)，
∴A1(3,1)，B1(1,−1)，C1(4,−2)，
故答案为：A1(3,1)，B1(1,−1)，C1(4,−2)；
(2)△A1B1C1如图所示；

(3)如图，连接OA，OA1，AA1，
△AOA1的面积=6×3−12×3×3−12×3×1−12×6×2
=18−92−32−6，
=6．
【点评】
本题考查了利用平移变换作图，三角形的面积等知识，熟练掌握网格结构，准确找出对应点的位置是解本题的关键．  
22.【答案】解：(1)∵OA⊥OB，
∴∠AOB=90°，
∵∠AOC=2∠BOC，∠AOC+∠BOC=90°，
∴2∠BOC+∠BOC=90°
∴∠BOC=30°；
(2)证明：∵∠AOB=90°，∠BOC=30°；
∴∠AOC=60°
又∵∠COD=60°．
∴∠AOC=∠COD，
∴OC平分∠AOD． 
【解析】(1)根据垂直的定义得出∠AOB=90°，根据∠AOC=2∠BOC，∠AOC+∠BOC=90°，得出∠BOC；
(2)由(1)的结论得出∠AOC=60°，进而得出∠AOC=∠COD，即可得出OC平分∠AOD．
本题考查了垂直的定义，角平分线的定义，数形结合是解题的关键．

23.【答案】解：(1)∵一个正数的两个不同平方根分别是a+3与2a−15，
∴a+3+2a−15=0，
解得a=4，
∴这个数一个平方根为4+3=7，
∴这个数为72=49；
(2)∵x，y为实数，y= x−9− 9−x+4，
∴x−9≥09−x≥0，
∴x≥9x≤9，
∴x=9，
∴y=4，
∴ xy
= 9×4
=6，
∴ xy的平方根为± 6． 
【解析】(1)先根据正数的两个平方根互为相反数，得出a+3+2a−15=0，求出a的值，得出这个数的一个平方根，即可得出这个正数；
(2)先根据二次根式有意义的条件得出x=9，从而求出y=4，代入求出 xy= 9×4=6，即可得出答案．
本题主要考查了平方根的定义，二次根式有意义的条件，解题的关键是熟练掌握正数的两个平方根互为相反数，二次根式中的被开方数为非负数．

24.【答案】解：(1)如图：过点C作CD⊥x轴，垂足为D，

∵C(−1,−3)，
∴CD=3，
∴点C到x轴的距离为3；
(2)连接AB，

∵A(−2,3)，B(4,3)，
∴AB//x轴，
∴AB=4−(−2)=4+2=6，
∴A、B之间的距离为6；
(3)过点C作CE⊥AB，垂足为E，设AB与y轴相交于点F，

∵点P在y轴上，
∴设点P的坐标为(0,m)，
∵A(−2,3)，B(4,3)，C(−1,−3)，
∴CE=3−(−3)=3+3=6，F(0,3)，
∴PF=|x−3|，
∵S△ABP=13S△ABC，
∴12AB⋅PF=13×12AB⋅CE，
∴PF=13CE，
∴PF=2，
∴|x−3|=2，
解得：x=5或x=1，
∴点P的坐标为(0,5)或(0,1)． 
【解析】(1)过点C作CD⊥x轴，垂足为D，根据点C的坐标即可解答；
(2)连接AB，根据已知可得AB//x轴，然后根据点A，B的坐标，进行计算即可解答；
(3)过点C作CE⊥AB，垂足为E，设AB与y轴相交于点F，根据已知可设点P的坐标为(0,m)，再根据已知易得CE=6，F(0,3)，从而可得PF=|x−3|，然后根据三角形的面积公式，进行计算即可解答．
本题考查了三角形的面积，坐标与图形的性质，熟练掌握三角形的面积公式是解题的关键．

25.【答案】解：(1)设甲乙两队同时施工，共同完成全部任务需要x天
根据题意得(230+230+115)x=4600，
解得x=8，
答：甲乙两队同时施工，共同完成全部任务需要8天；
(2)设乙队需再施工y天才能完成任务
根据题意得5(230+230+115)+(230+115)y=4600，
解得y=5，
答：乙队需再施工5天才能完成任务． 
【解析】(1)设甲乙两队同时施工，共同完成全部任务需要x天，根据题意列出方程求解即可；
(2)设乙队需再施工y天才能完成任务，根据甲乙两队共同施工5天，剩余的部分由乙队单独完成列方程求解即可．
本题主要考查了一元一次方程的应用，认真审题、找出题中的等量关系是解答本题的关键．

26.【答案】(1)解：AB//CD，理由如下：
∵∠1与∠2互补，
∴∠1+∠2=180°，
又∵∠1=∠AEF，∠2=∠CFE，
∴∠AEF+∠CFE=180°，
∴AB//CD；
(2)证明：由(1)知，AB//CD，
∴∠BEF+∠EFD=180°．
又∵∠BEF与∠EFD的角平分线交于点P，
∴∠FEP+∠EFP=12(∠BEF+∠EFD)=90°，
∴∠EPF=90°，即EG⊥PF．
∵GH⊥EG，
∴PF//GH；
(3)解：没发生变化，理由：
∵∠PHK=∠HPK，
∴∠PKG=2∠HPK．
又∵GH⊥EG，
∴∠KPG=90°−∠PKG=90°−2∠HPK．
∴∠EPK=180°−∠KPG=90°+2∠HPK．
∵PQ平分∠EPK，
∴∠QPK=12∠EPK=45°+∠HPK．
∴∠HPQ=∠QPK−∠HPK=45°．
答：∠HPQ的度数为45°． 
【解析】(1)根据同旁内角互补，两条直线平行即可判断直线AB与直线CD平行；
(2)先根据两条直线平行，同旁内角互补，再根据∠BEF与∠EFD的角平分线交于点P，可得∠EPF=90°，进而证明PF//GH；
(3)根据角平分线定义，及角的和差计算即可求得∠HPQ的度数．
本题考查了平行线的判定和性质、余角和补角，解决本题的关键是综合运用角平分线的定义、平行线的性质、余角和补角．