初中数学湘教版七年级下册6.1.2中位数一等奖教学设计

6.1.2中位数

【知识与技能】

1.在现实情景中认识中位数的统计意义及优、缺点.

2.能在具体情景中运用中位数处理一些实际问题.

【过程与方法】

在探索知识的过程中，培养学生分析数据的能力，在数学的学习中发现规律，培养学生用数据说话的习惯.

【情感态度】

关注学生的情感体验，让学生感受到数学的魅力，从而认识到数学的价值.

【教学重点】

理解中位数的意义并会求一组数据的中位数.

【教学难点】

理解一组数据的平均数、中位数的区别.

一、情景导入，初步认知

1.什么是平均数？什么是加权平均数？

2.它们分别如何来求？

【教学说明】对前面的知识进行复习，为本节课的教学作准备.

二、思考探究，获取新知

1.张某管理一家餐厅，下面是该餐馆所有工作人员的月工资情况：

张某：15000元；会计：1800元；

厨师甲：2500元；厨师乙：2000元；杂工甲：1000元；杂工乙：1000元；

服务员甲：1500元；服务员乙：1200元；服务员丙：1000元.

计算他们的平均工资，这个平均工资能反映该餐馆员工在这个月收入的一般水平吗？

该餐馆全体员工的平均工资为：

=(15000+1800+2500+2000+1000+1000+1500+1200+1000)÷9=3000(元).

实际上，3000元不能代表该餐馆员工在这个月的收入一般水平，因为除了张某外员工中工资最高的厨师甲的月收入2500元都小于这个平均数.

若不计张某的工资，剩下员工的工资平均数为：

=(1800+2500+2000+1000+1000+1500+1200+1000)÷8=1500(元)

不计张某的工资，1500元能代表餐馆工作人员在这个月收入的一般水平.

2.还有没有别的方法呢？

【教学说明】引导学生分析：我们可以把餐馆中人员的月收入按从小到大(或从大到小)排列，位于中间的数据，也能比较合理地反映该餐馆员工的月收入水平.

3.我们可以把餐馆工作人员的月收入按从小到大的顺序排列：

1000、1000、1000、1200、1500、1800、2000、2500、15000

位于中间的数据即第5个数据1500就比较合理地反映了该餐馆员工的月收入水平.

像上述例子那样，将一组数据按大小依次排列，把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.中位数代表了一组数据的数值大小的“中点”，当一组数据的个数较小时，中位数容易求出，这是中位数的优点，但中位数没有利用数据中的所有信息，因此，有时它可能不是很有效的.

4.求下列两组数据的中位数：

(1)14、11、13、10、17、16、28；

(2)453、442、450、445、446、457、448、449、451、450；

解：(1)把组数据从小到大排列：

10、11、13、14、16、17、28

位于中间的数是14，因此这组数据的中位数是14.

(2)把组数据从小到大排列：

442、445、446、448、449、450、450、451、453、457

位于中间的两个数是449和450，这两个数的平均数是449.5，因此这组数据的中位数是449.5.

根据上面的例题，你能总结求一组数据的中位数的方法吗？

【归纳结论】将这组数据按从小到大的顺序排列，如果这组数据有奇数个，则中间的这个数就是这组数据的中位数；如果这组数据有偶数个，则中间的两个数的平均数就是这组数据的中位数.

中位数有什么作用呢？

【归纳结论】中位数把一组数据分成相同数目的两部分，其中一部分都小于或等于中位数，而另一部分都大于或等于中位数.因此中位数常常用来描述“中间位置”或“中等水平”，但中位数没有利用数据组中的所有信息.

【教学说明】在自主解决问题的过程中，要充分体现以学生为主体，教师为主导的教学意识.当学生迷惑时教师适时地提出问题，充分体现教师的主导作用，使学生在比较中自己发现什么数是中位数，以及找中位数应先排列大小.

三、运用新知，深化理解

1.某班8名学生完成作业所需时间分别为：75，70，90，70，70，58，80，55(单位：分)，则这组数据的中位数为____，平均数为____.

答案：70分，71分.

2.已知一组数据1,0,-3,2,-6,5，这组数据的中位数为____.

答案：0.5.

3.数据10，10，x，8的中位数与平均数相等，这组数据的中位数是___.

答案：9或10.

4.把9个数按从小到大的顺序排列,其平均数是9,如果这组数中前5个数的平均数是8,后5个数的平均数是10,则这9个数的中位数是___.

答案：9.

5.一组数据是23，27，20，18，12，x，它的中位数是21，则数据x是(D)

A.23    B.21

C.不小于23数  D.以上都不是

6.我市部分学生参加了2014年全国初中数学竞赛决赛，并取得优异成绩.已知竞赛成绩分数都是整数，试题满分为140分，参赛学生的成绩分数分布情况如下：

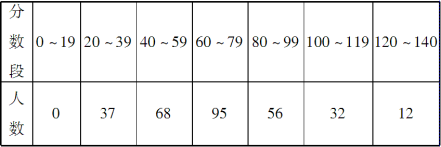
请根据以上信息解答下列问题：

(1)全市共有多少人参加本次数学竞赛决赛？最低分和最高分在什么分数范围？

(2)经竞赛组委会评定，竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励，求我市参加本次竞赛决赛考生的获奖比例；

(3)决赛成绩分数的中位数落在哪个分数段内？

(4)上表还提供了其他信息，例如：“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.

解：(1)全市共有300名学生参加本次竞赛决赛，最低分在20~39之间，最高分在120~140之间；

(2)本次决赛共有195人获奖，获奖率为65%；

(3)决赛成绩的中位数落在60~79分数段内;

(4)如“120分以上有12人；60至79分数段的人数最多”等.

7.某中学开展“八荣八耻”演讲比赛活动，九(1)，九(2)班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据图填写下表：

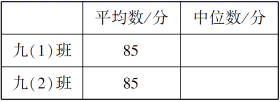
(2)结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好？

(3)如果在每班参加复赛的选手中分别选出2人参加决赛，你认为哪个班的实力更强?

解：(1)85，80.

(2)两个班平均数相同，九(1)班中位数高，所以九(1)班成绩好些.

(3)九(2)班实力更强一些.

【教学说明】通过练习巩固本节课数学内容.四、师生互动,课堂小结

先小组内交流收获和感想，而后以小组为单位派代表进行总结.教师作以补充.

1.布置作业:教材第147页“习题6.1”中第4题.

2.完成同步练习册中本课时的练习.

教师应该把学生放在中心地位，努力创设适合学生学习的情境，让学生投入到自主学习中去，在自主活动中投入智力参与，获得对新知识的个人体验，达到把课本知识转化为学生自己知识的目的，做一个学生学习的帮助者.