专题01 两个计数原理-2024年新高考数学题型全归纳之排列组合

这是一份专题01 两个计数原理-2024年新高考数学题型全归纳之排列组合，文件包含专题01两个计数原理解析版docx、专题01两个计数原理原卷版docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。
专题01 两个计数原理
类型一、加法原理
例1．（2023·全国·高三专题练习）某奥运村有，，三个运动员生活区，其中区住有人，区住有人，区住有人已知三个区在一条直线上，位置如图所示奥运村公交车拟在此间设一个停靠点，为使所有运动员步行到停靠点路程总和最小，那么停靠点位置应在（    ）

A．区 B．区 C．区 D．，两区之间
【答案】A
【解析】若停靠点为区时，所有运动员步行到停靠点的路程和为：米；
若停靠点为区时，所有运动员步行到停靠点的路程和为：米；
若停靠点为区时，所有运动员步行到停靠点的路程和为：米；
若停靠点为区和区之间时，设距离区为米，所有运动员步行到停靠点的路程和为：
，
当取最小值，故停靠点为区．
故选：A
例2．（2023·全国·高三专题练习）现有5幅不同的油画，2幅不同的国画，7幅不同的水彩画，从这些画中选一幅布置房间，则不同的选法共有（    ）
A．7种 B．9种 C．14种 D．70种
【答案】C
【解析】分为三类:
从国画中选，有2种不同的选法;从油画中选，有5种不同的选法;从水彩画中选，有7种不同的选法，
根据分类加法计数原理，共有5+2+7= 14(种)不同的选法;
故选：C
例3．（2023·全国·高三专题练习）2010年世界杯足球赛预计共有24个球队参加比赛，第一轮分成6个组进行单循环赛（在同一组的每两个队都要比赛），决出每个组的一、二名，然后又在剩下的12个队中按积分取4个队（不比赛），共计16个队进行淘汰赛来确定冠亚军，则一共需比赛（    ）场次．
A．53 B．52 C．51 D．50
【答案】C
【解析】第一轮分成6个组进行单循环赛共需要场比赛，淘汰赛有如下情况：16进8需要8场比赛，8进4需要4场比赛，4进2需要2场比赛，确定冠亚军需要1场比赛，共需要场比赛
故选：C．
例4．（2023·全国·高三专题练习）在北京冬奥会短道速滑混合团体2000米接力决赛中，中国队成功夺冠，为中国体育代表团夺得本届冬奥会首金.短道速滑男女接力赛要求每队四名运动员，两男两女，假设男女队员间隔接力，且每位队员只上场一次，则不同的上场次序的种数为（    ）
A．8 B．16 C．18 D．24
【答案】A
【解析】把问题分类：（1）以男运动员排第一位，上场次序的种数为：；（2）以女运动员排第一位，上场次序的种数为：；总的上场次序种数合计为：
故选：A
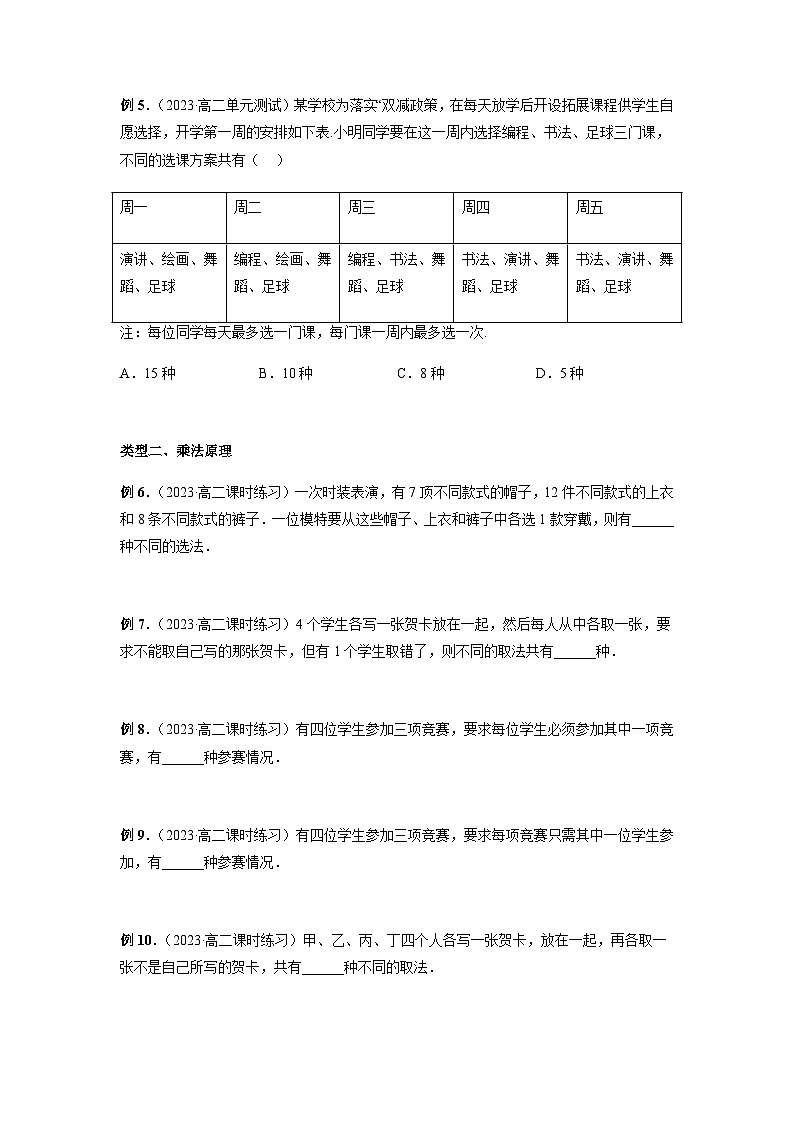
例5．（2023·高二单元测试）某学校为落实“双减政策，在每天放学后开设拓展课程供学生自愿选择，开学第一周的安排如下表.小明同学要在这一周内选择编程、书法、足球三门课，不同的选课方案共有（    ）
周一
周二
周三
周四
周五
演讲、绘画、舞蹈、足球
编程、绘画、舞蹈、足球
编程、书法、舞蹈、足球
书法、演讲、舞蹈、足球
书法、演讲、舞蹈、足球
注：每位同学每天最多选一门课，每门课一周内最多选一次.
A．15种 B．10种 C．8种 D．5种
【答案】A
【解析】若周二选编程，则选课方案有（种）；若周三选编程，则选课方案有（种）.综上，不同的选课方案共有（种）.
故选:A.
类型二、乘法原理
例6．（2023·高二课时练习）一次时装表演，有7顶不同款式的帽子，12件不同款式的上衣和8条不同款式的裤子．一位模特要从这些帽子、上衣和裤子中各选1款穿戴，则有______种不同的选法．
【答案】672
【解析】模特完成穿戴需要分三步：第一步，选择帽子，共有7种选择；第二步，选择上衣，共有12种选择；第三步，选择裤子，共有8种选择；根据乘法原理，共有种.
故答案为：
例7．（2023·高二课时练习）4个学生各写一张贺卡放在一起，然后每人从中各取一张，要求不能取自己写的那张贺卡，但有1个学生取错了，则不同的取法共有______种．
【答案】8
【解析】有1个学生取错了，有种可能，另外三人假设为甲、乙、丙，按要求取贺卡，甲先去拿一个贺卡，有2种取法，假设甲拿的是乙写的贺卡，接下来让乙去拿，乙此时只能拿丙的贺卡，而丙最后拿甲的贺卡，则不同的取法共种.
故答案为：8．
例8．（2023·高二课时练习）有四位学生参加三项竞赛，要求每位学生必须参加其中一项竞赛，有______种参赛情况．
【答案】81
【解析】根据乘法分步原理，每位学生都有三种选择方案，故有种.
故答案为：
例9．（2023·高二课时练习）有四位学生参加三项竞赛，要求每项竞赛只需其中一位学生参加，有______种参赛情况．
【答案】64
【解析】根据题意，每一项竞赛都有4位同学可以选择，故有种参赛情况.
故答案为：
例10．（2023·高二课时练习）甲、乙、丙、丁四个人各写一张贺卡，放在一起，再各取一张不是自己所写的贺卡，共有______种不同的取法．
【答案】9
【解析】第一步甲取1张不是自己所写的那张贺卡，有3种取法；
第二步由甲取出的那张贺卡的供卡人取，也有3种不同取法；
第三步由剩余两人中任1个人取，此时只有1种取法；
第四步最后1个人取，只有1种取法.根据分步计数原理可得种.
故答案为：9
例11．（2023·高二课时练习）某酒店的大楼有18层，每层12个房间，如果每个房间都安装一个电话分机，那么用1、2、3、4、5、6这六个数字所组成的三位数作为各分机的号码，是否够用？
【解析】由题知，房间数为，
这六个数字组成的号码个数为，
所以号码刚好够用．

例12．按序给出，两类元素，类中的元素排序为甲、乙、丙、丁、戊、己、庚、辛、壬、癸，类中的元素排序为子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥．在，两类中各取1个元素组成1个排列，求类中选取的元素排在首位，类中选取的元素排在末位的排列的个数．类的10个元素叫作天干，类的12个元素叫作地支．两者按固定顺序相配，形成古代纪年历法，求天干各地支相配可形成的纪年历法可以表示多少年.
【解析】从类中选取一个元素排在首位的选法有10种，从类中选取一个元素排在末位的选法有12种，由分步乘法计数原理可得所有排列的个数为120种.
例13．某班有男生30名、女生24名，从中任选男生和女生各1名代表班级参加比赛，共有多少种不同的选法？
【答案】720.
【解析】
第一步，从30名男生中选出1人，有30种不同选法；
第二步，从24名女生中选出1人，有24种不同选法.
根据分步乘法计数原理，共有不同选法的种数有.
所以共有720种不同的选法.

类型三、基本计数原理的综合应用
例14．（2023秋·河北·高二河北省文安县第一中学校考期末）如图，要让电路从A处到B处接通，不同的路径条数为（    ）

A．5 B．7 C．8 D．12
【答案】C
【解析】要让电路从A处到B处接通，不同的路径条数为．
故选：C．
例15．（2023·高二单元测试）一杂技团有8名会表演魔术或口技的演员，其中有6人会表演口技，有5人会表演魔术，现从这8人中选出2人上台表演，1人表演口技，1人表演魔术，则不同的安排方法有______种．
【答案】27
【解析】由题可知有2人只会表演魔术，3人只会表演口技，3人既会表演魔术又会表演口技，
针对只会表演魔术的人讨论，先从只会表演魔术的人表演魔术有2种选择，再从其他的6人选1人表演口技有6种选择，故共有种选择；
不选只会表演魔术的人，从既会表演魔术又会表演口技的3人中选1人表演魔术，有3种选择，
再从只会表演口技的3人和既会表演魔术又会表演口技的剩余2人选1人表演口技，有5种选择，
故共有种选择；
所以不同的安排方法有种.
故答案为：27.
例16．（2023·全国·高三专题练习）如图，一条电路从A处到B处接通时，可以有_____________条不同的线路（每条线路仅含一条通路）．

【答案】
【解析】依题意按上、中、下三条线路可分为三类，
上线路中有种，
中线路中只有种，
下线路中有（种．
根据分类计数原理，共有（种．
故答案为：．
例17．（2023春·四川绵阳·高三绵阳中学校考阶段练习）小小的火柴棒可以拼成几何图形，也可以拼成数字．如下图所示，我们可以用火柴棒拼出1至9这9个数字比如：“1”需要2根火柴棒，“7”需要3根火柴棒．若用8根火柴棒以适当的方式全部放入右面的表格中

（没有放入火柴棒的空位表示数字“0”），那么最多可以表示无重复数字的三位数有______个

【答案】20
【解析】由题意可得，用2根火柴棒表示数字1，3根火柴棒表示数字7，4根火柴棒表示数字4，5根火柴棒表示数字2，3或5，6根火柴棒表示数字6或9，7根火柴棒表示数字8，
数字不重复，因此8根火柴棒只能分成两类：2和6，3和5，组成两个数字，还有数字只能为0，
这样组成的无重复数字的三位数个数为：．
故答案为：20
例18．（2023·全国·高三专题练习）某学校每天安排4项课后服务供学生自愿选择参加．学校规定：
（1）每位学生每天最多选择1项；
（2）每位学生每项一周最多选择1次．学校提供的安排表如下：
时间
周一
周二
周三
周四
周五
课后服务
音乐、阅读、
体育、编程
口语、阅读、
编程、美术
手工、阅读、
科技、体育
口语、阅读、
体育、编程
音乐、口语、
美术、科技
若某学生在一周内共选择了阅读、体育、编程3项，则不同的选择方案共有______种．（用数值表示）
【答案】14
【解析】由题知：周一、二、三、四均可选阅读，体育在周一、三、四，
编程在周一、二、四.
①若周一选编程，则体育在周三或周四，故为种，
阅读在剩下的两天中选为种，共有种方案.
②若周二选编程，则体育在周一，周三或周四，故为种，
阅读在剩下的两天中选为种，共有种方案.
③若周四选编程，则体育在周一或周三，故为种，
阅读在剩下的两天中选为种，共有种方案.
综上，共有种方案.
故答案为：
例19．（2023·高二课时练习）书架上放有3本不同的数学书，5本不同的语文书，6本不同的英语书．
(1)从这些书中任取一本，有多少种不同的取法？
(2)从这些书中取数学书、语文书、英语书各一本，有多少种不同的取法？
(3)从这些书中取不同科目的书共两本，有多少种不同的取法？
【解析】（1）由于书架上有本书，
则从中任取一本，共有14种不同的取法.
（2）由题意分步完成，
第一步：取任取一本数学书，有3种取法；
第二步：取任取一本语文书，有5种取法；
第三步：取任取一本英语书，有6种取法；
由分步乘法计数原理得共有种不同的取法.
（3）取两本不同科目的数，可以分三种情况：
①一本数学书和一本语文书，有种情况；
②一本数学书和一本英语书，有种情况；
③一本语文书和一本英语书，有种情况；
根据分类加法计数原理，共有种情况.
例20．（2023·高二单元测试）在某次国际高峰论坛上，组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问，要求这3个媒体团中既有国内媒体团又有国外媒体团，且国内媒体团不能连续提问，则不同的提问方式的种数是多少？
【解析】由题，根据选取方式可分为2种情况：
2个国内媒体团和1个国外媒体团，选取方式有种，提问方式有种，共种；
1个国内媒体团和2个国外媒体团，选取方式有种，提问方式有种，共种.
综上，共种