2023年高考真题和模拟题数学分项汇编（全国通用）专题02+平面向量

专题02  平面向量

（新课标全国Ⅰ卷）1．已知向量，若，则（    ）

A． B．

C． D．

（新课标全国Ⅱ卷）2．已知向量，满足，，则______．

（全国乙卷数学（文））3．正方形的边长是2，是的中点，则（    ）

A． B．3 C． D．5

（全国乙卷数学（理））4．已知的半径为1，直线PA与相切于点A，直线PB与交于B，C两点，D为BC的中点，若，则的最大值为（    ）

A． B．

C． D．

（全国甲卷数学（文））5．已知向量，则（    ）

A． B． C． D．

（全国甲卷数学（理））6．向量，且，则（    ）

A． B． C． D．

（新高考天津卷）7．在中，，，点为的中点，点为的中点，若设，则可用表示为_________；若，则的最大值为_________．

1．（2023·湖南长沙·雅礼中学校考模拟预测）已知向量，满足，且，，则（    ）

A．5 B．3 C．2 D．1

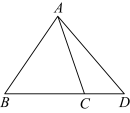
2．（2023·湖北武汉·华中师大一附中校考模拟预测）如图，在中，点在的延长线上，，如果，那么（    ）

A． B．

C． D．

3．（2023·山东潍坊·三模）已知平面向量与的夹角是，且，则（    ）

A． B． C． D．

4．（2023·陕西安康·陕西省安康中学校考模拟预测）已知向量，满足，，则与的夹角为（    ）

A． B． C． D．

5．（2023·重庆万州·重庆市万州第三中学校考模拟预测）已知向量，，若，则向量在上的投影向量的模长为___________.

6．（2023·重庆·校联考三模）已知点，，若圆上存在点P满足，则实数a的取值的范围是____________．  

7．（2023·全国·模拟预测）已知平面向量，满足，，，则，夹角的余弦值为（    ）

A． B． C． D．

8．（2023·云南保山·统考二模）已知向量，满足，则在方向上的投影向量为（    ）

A． B． C． D．

9．（2023·广东佛山·校考模拟预测）梯形中，，已知，则（    ）

A． B． C． D．

10．（2023·广东·校联考模拟预测）将向量绕坐标原点顺时针旋转得到，则（    ）

A． B．

C． D．

11．（2023·广西·校联考模拟预测）已知和是两个正交单位向量，，且，则（    ）

A．2或3 B．2或4 C．3或5 D．3或4

12．（2023·四川成都·石室中学校考模拟预测）已知平面向量，，的夹角为，，则实数（    ）

A． B．1 C． D．

13．（2023·北京·统考模拟预测）若向量，，则与的夹角等于（    ）

A． B． C． D．

14．（2023·山西阳泉·阳泉市第一中学校校考模拟预测）已知向量，，，且，则实数（    ）

A．-1 B．0 C．1 D．任意实数

15．（2023·浙江·统考模拟预测）已知，若，则（    ）

A． B．

C． D．

（多选）16．（2023·山东聊城·统考三模）已知向量，满足，，则与的夹角可以为（    ）

A． B． C． D．

17．（2023·河南开封·统考三模）已知向量，，若，则______.

18．（2022·陕西西安·统考模拟预测）若向量，不共线，且，则________.

19．（2023·河南驻马店·统考三模）已知平面向量满足,且，则=_________________ ．

20．（2023·河南·校联考模拟预测）向量的夹角为，定义运算“”：，若，则的值为___________.