江苏省镇江市2022-2023学年八年级上学期期末数学试卷

这是一份江苏省镇江市2022-2023学年八年级上学期期末数学试卷，共9页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。

2022-2023学年江苏省镇江市八年级（上）期末数学试卷
一、填空题（本大题共12小题，每小题2分，共24分）
1.4的平方根是______．
2.在平面直角坐标系中，点A(−3,5)在第______ 象限．
3.已知点P(a,4)在一次函数y=2x的图像上，则a= ______ ．
4.等腰三角形的一个内角为100°，这个等腰三角形底角的度数为______．
5.点M(2,−3)到x轴的距离是______．
6.已知点A(−5,y1)、B(3,y2)都在一次函数y=−8x+7的图像上，比较大小：y1 ______ y2．
7.在学习了《探索三角形全等的条件》后，小龙编了这样一个题目：“如图，已知AB=CD，∠A=∠D，AO=DO，求证：△ABO≌△DCO.”老师说他的已知条件给多了，你帮他去掉一个已知条件：______ .(写出一个即可)

8.如图，△AOD≌△BOC，∠A=30°，∠C=50°，∠AOC=150°，则∠COD= ______ °.

9.2022年11月30日，神舟十五号载人飞船上的3名航天员顺利进驻中国空间站，与神舟十四号航天员乘组首次实现“太空会师”.神舟十五号载人飞船飞行时速是28182.4公里/小时，由四舍五入法得到近似数为2.8×104公里/小时，该近似数精确到______ 位.
10.在平面直角坐标系中，一次函数y1=ax+b(a≠0)与y2=mx+n(m≠0)的图像如图所示，则关于x的不等式ax+b>mx+n的解集为______ ．

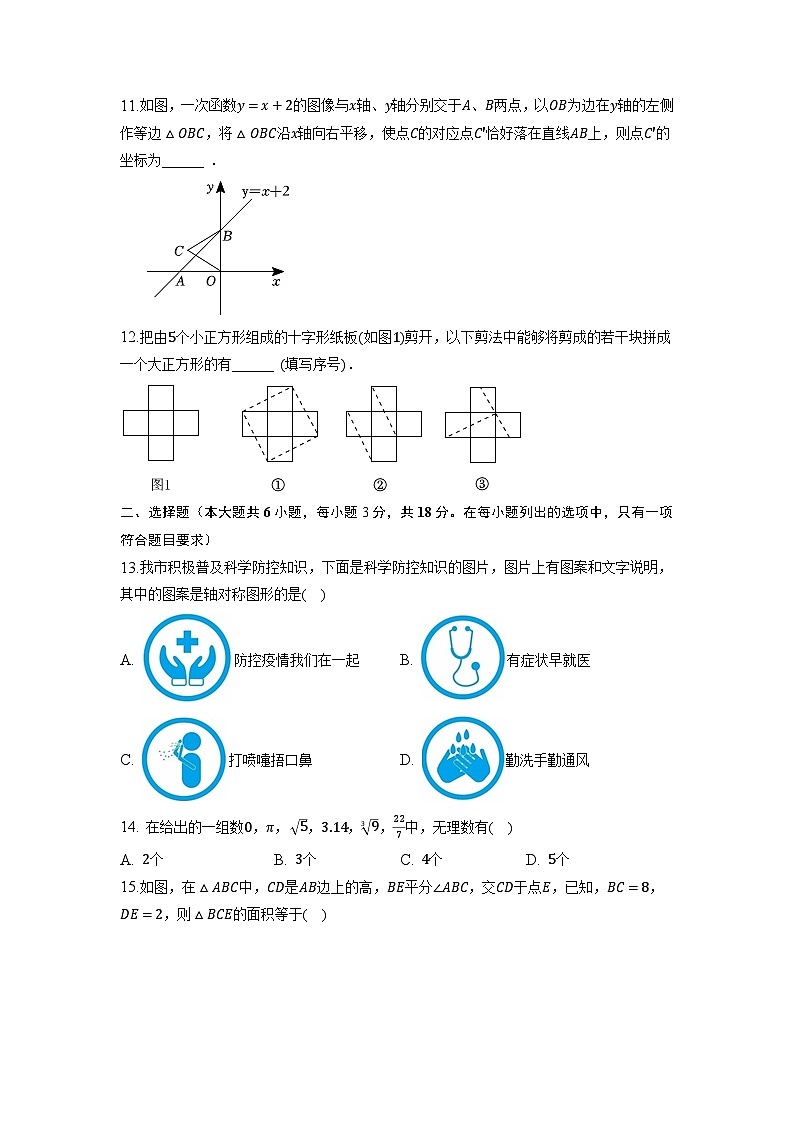
11.如图，一次函数y=x+2的图像与x轴、y轴分别交于A、B两点，以OB为边在y轴的左侧作等边△OBC，将△OBC沿x轴向右平移，使点C的对应点C′恰好落在直线AB上，则点C′的坐标为______ ．

12.把由5个小正方形组成的十字形纸板(如图1)剪开，以下剪法中能够将剪成的若干块拼成一个大正方形的有______ (填写序号)．

二、选择题（本大题共6小题，每小题3分，共18分。在每小题列出的选项中，只有一项符合题目要求）
13.我市积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是(    )
A. 防控疫情我们在一起 B. 有症状早就医
C. 打喷嚏捂口鼻 D. 勤洗手勤通风
14. 在给出的一组数0，π， 5，3.14，39，227中，无理数有(    )
A. 2个 B. 3个 C. 4个 D. 5个
15.如图，在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，已知，BC=8，DE=2，则△BCE的面积等于(    )

A. 4 B. 6 C. 8 D. 10
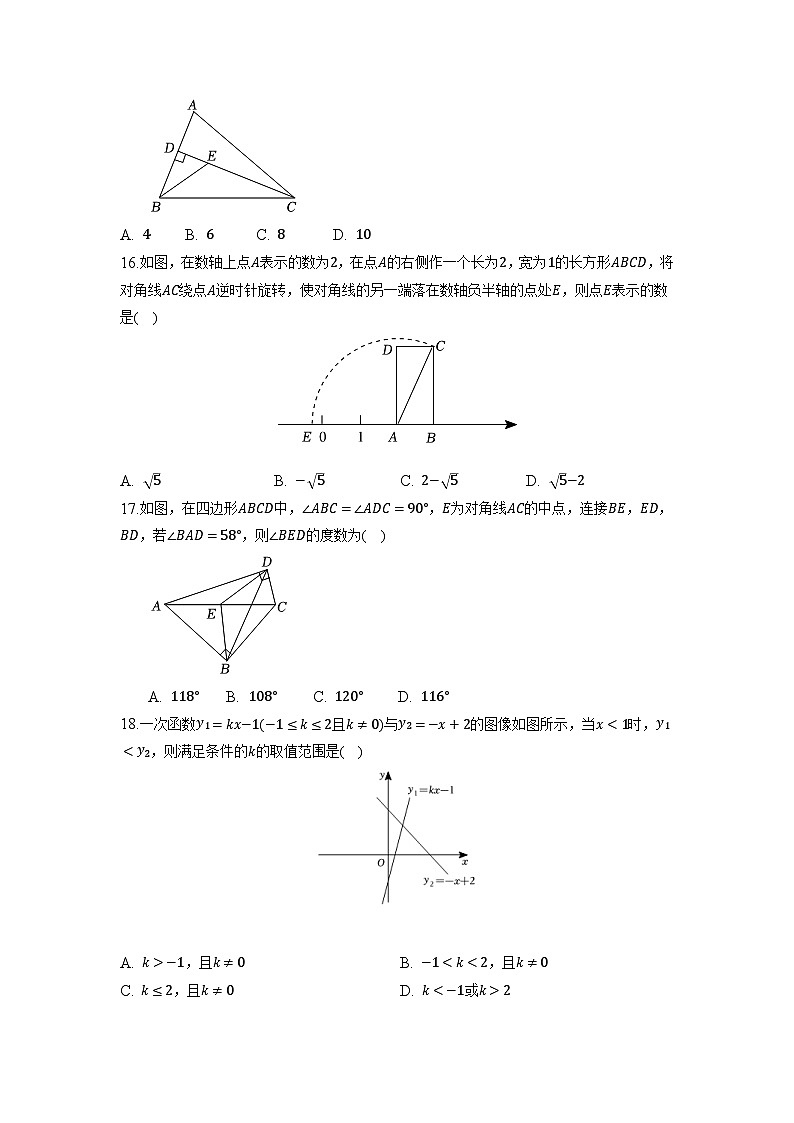
16.如图，在数轴上点A表示的数为2，在点A的右侧作一个长为2，宽为1的长方形ABCD，将对角线AC绕点A逆时针旋转，使对角线的另一端落在数轴负半轴的点处E，则点E表示的数是(    )

A. 5 B. − 5 C. 2− 5 D. 5−2
17.如图，在四边形ABCD中，∠ABC=∠ADC=90°，E为对角线AC的中点，连接BE，ED，BD，若∠BAD=58°，则∠BED的度数为(    )

A. 118° B. 108° C. 120° D. 116°
18.一次函数y1=kx−1(−1≤k≤2且k≠0)与y2=−x+2的图像如图所示，当x<1时，y1
A. k>−1，且k≠0 B. −1 C. k≤2，且k≠0 D. k<−1或k>2

三、解答题（本大题共8小题，共78分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题12分)(1)计算： 16+|2− 3|−327；
(2)求下列各式中的x：
①3x2=27；
②(x−3)3+125=0．
20. (本小题8分)已知：如图，ED⊥AB，FC⊥AB，垂足分别为D、C，AC=BD，且AE=BF．
求证：(1)△ADE≌△BCF；
(2)AE//BF．

21. (本小题9分)如图，在平面直角坐标系中，点A(1,−2)、B(4,−2)关于直线l对称，点C的坐标是(−2,1)，点C关于直线l的对称点为点C′．
(1)△ABC的面积等于______ ；点C′的坐标为______ ；
(2)在直线l上找一点P，使得PB+PC′最短，则PB+PC′的最小值等于______ ．

22. (本小题9分)将正比例函数y=3x的图像平移后经过点(1,4)．
(1)求平移后的函数表达式；
(2)求平移后函数的图像与坐标轴围成的三角形的面积．
23. (本小题8分)如图，已知Rt△ABC，∠C=90°，BC=3，点P为边AC上一点且CP=1．
(1)请用直尺和圆规在边BC上求作一点E，使CE+EP=BC；(要求：保留作图痕迹，不写作法)
(2)求CE的长．

24. (本小题12分)为了帮助经济相对薄弱村发展经济，将真正的实惠带给消费者，某市在各菜市场开设了“爱心助农销售专区”.现从某村购进苹果和橙子进行销售，进价分别为每箱40元和60元，该专区决定苹果以每箱60元出售，橙子以每箱88元出售．
(1)若购进苹果120箱，橙子200箱，可获利______ 元；
(2)为满足市场需求，需购进这两种水果共1000箱，设购进苹果m箱，获得的利润为W元．
①请求出获利W(元)与购进苹果箱数m(箱)之间的函数表达式；
②若此次活动该村获润不低于25000元，则最多销售多少箱苹果？
25. (本小题12分)如图1，在四边形ABCD中，∠B=90°，AD//BC，AB=4，AD=6.若动点P从点B出发，以每秒2个单位长度的速度沿着BC→CD→DA的路线向终点A运动.设点P的运动时间为t秒，图2是点P出发t秒后，△ABP的面积S与t的函数图像．
(1)a= ______ ，b= ______ ；
(2)求MN所在直线对应的函数表达式；
(3)运动几秒后，△ABP的面积为14？

26. (本小题8分)某学校社团设计了一个寻宝游戏，给出了一份寻宝启示：如图，已知点A(2,1)，将OA绕着点A顺时针旋转90°，点O的对应点为点A1，再将OA1绕着点A1顺时针旋转90°，点O的对应点为点A2，依次下去…，宝藏恰好藏在点A5的位置，并且一次函数y=2x−4的图像经过点A5．
(1)直接写出点A1的坐标______ ；
(2)求宝藏点A5的坐标．


参考答案与解析
选择、填空题答案
1.±2 2.二 3.2 4.40° 5.3 6.> 7.AO=DO或AB=CD
8.50 9.千 10.x>3 11.（-1，1） 12.①③
13
14
15
6
17
18
A
B
C
C
D
B
19.解：(1) 16+|2− 3|−327
=4+2− 3−3
=3− 3.
(2)①3x2=27，
∴x2=9，∴x=±3.
②(x−3)3+125=0，
∴(x−3)3=−125，
∴x−3=−5，∴x=−2． 
20.证明：(1)∵ED⊥AB，FC⊥AB，
∴∠ADE=∠BCF=90°.
∵AC=BD，∴AC+CD=BD+CD，∴AD=BC.
在Rt△ADE和Rt△BCF中，
∴Rt△ADE≌Rt△BCF(HL).
(2)由(1)，得△AED≌△BFC，
∴∠A=∠B，∴AE//BF． 
21.解：（1）92  (7,1) ；（2）3 5 
22.解：(1)设平移后的函数表达式为y=3x+b，
由题意，得4=3×1+b，解得b=1．
∴函数表达式为y=3x+1．
(2)令x=0，则y=1；
令y=0，则3x+1=0，解得x=−13，
∴直线y=3x+1与坐标轴的交点坐标为(−13,0)，(0,1).
∴平移后的函数图像与两坐标轴所围成的三角形的面积为12×13×1=16． 
23.解：(1)如图所示，点E即所求.

(2)设CE=x，则PE=3−x.
∵∠C=90°，∴CP2+EC2=PE2，
∴1+x2=(3−x)2，解得x=43，
∴EC的长为43． 
24.解：（1）8000 
(2)①根据题意，得W=(60−40)m+(88−60)(1000−m)=20m+28(1000−m)=−8m+28000，
∴获利W(元)与购进苹果箱数m(箱)之间的函数表达式为W=−8m+28000.
②由题意，得−8m+28000≥25000，解得m≤375.
答：此次活动该村获润不低于25000元，最多销售375箱苹果．
25.解：（1）92  7 
(2)当点P到达D点时，△ABP的面积S=12AB⋅AD=12×4×6=12，∴N(7,12).
由(1)，知M(92,18).
设MN所在直线对应的函数表达式为S=kt+b，
解得
∴MN所在直线对应的函数表达式为S=−125t+1445(92≤t≤7).
(3)根据题意分3种情况讨论：
①当点P在BC上运动时，
S△ABP=12×BP×AB=12×2t×4=4t(0 ∵△ABP的面积为14，∴4t=14，∴t=72；
②当点P在CD上运动时，
由(2)知S=−125t+1445(92≤t≤7)，
∴−125t+1445=14，∴t=376；
③当点P在AD上运动时，
S△ABP=12×AB×AP=12×4×(10×2−2t)=−4t+40(7 ∴−4t+40=14，解得t=（不符合题意，舍去）.
综上所述，t=72或t=376时，△ABP的面积为14．
26.解：（1）(1,3) 
过A点作BC⊥x轴于B点，过A1点作A1C⊥AB于C点，如图，则∠A1CA=∠ABO=90°，∴∠A1AC+∠AA1C=90°.∵将OA绕着点A顺时针旋转90°，点O的对应点为点A1，∴OA=A1A，∠A1AO=90°，
∴∠A1AC+∠OAB=90°，∴∠AA1C=∠OAB.在△AA1C和△OAB中，
∴△AA1C≌△OAB(AAS)，∴AC=OB=2，A1C=AB=1，∴OB−A1C=2−1，AB+AC=1+2=3，∴A1的坐标为(1,3).

(2) 如图，由题意，得△AOA1，△A1OA2，△A2OA3，△A3OA4，△A4OA5均为等腰直角三角形，
∴∠AOA1=∠A1OA2=∠A2OA3=∠A3OA4=∠A4OA5=45°，
∴∠A5OA1=180°，∴点A5与点A1在同一条直线上.
设直线OA1的表达式为y=kx，
将A1(1,3)代入，得k=3，∴直线OA1的表达式为y=3x.
∵一次函数y=2x−4的图像经过点A5，
∴点A5是直线y=3x和直线y=2x−4的交点，
解得
∴宝藏点A5的坐标为(−4,12)．