


选择性必修 第一册3.2 双曲线优秀课时作业
展开3.2.1双曲线及其标准方程
课程标准
核心素养
1.了解双曲线的实际背景,感受双曲线在刻画现实世界和解决实际问题中的作用.
2.了解双曲线的定义、几何图形和标准方程.
数学抽象
直观想象
知识点1 双曲线的定义
把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
注:1、集合语言表达式
双曲线就是下列点的集合:.常数要小于两个定点的距离.
2、对双曲线定义中限制条件的理解
(1)当||MF1|-|MF2||=2a>|F1F2|时,M的轨迹不存在.
(2)当||MF1|-|MF2||=2a=|F1F2|时,M的轨迹是分别以F1,F2为端点的两条射线.
(3)当||MF1|-|MF2||=0,即|MF1|=|MF2|时,M的轨迹是线段F1F2的垂直平分线.
(4)若将定义中的绝对值去掉,其余条件不变,则动点的轨迹为双曲线的一支.具体是哪一支,取决于与的大小.
①若,则,点的轨迹是靠近定点的那一支;
②若,则,点的轨迹是靠近定点的那一支.
【即学即练1】已知A(0,-5),B(0,5),|PA|-|PB|=2a,当a=3或5时,P点的轨迹为( )
A.双曲线或一条直线
B.双曲线或两条直线
C.双曲线一支或一条直线
D.双曲线一支或一条射线
【即学即练2】已知M(-2,0),N(2,0),|PM|-|PN|=4,则动点P的轨迹是( )
A.双曲线 B.双曲线左支
C.一条射线 D.双曲线右支
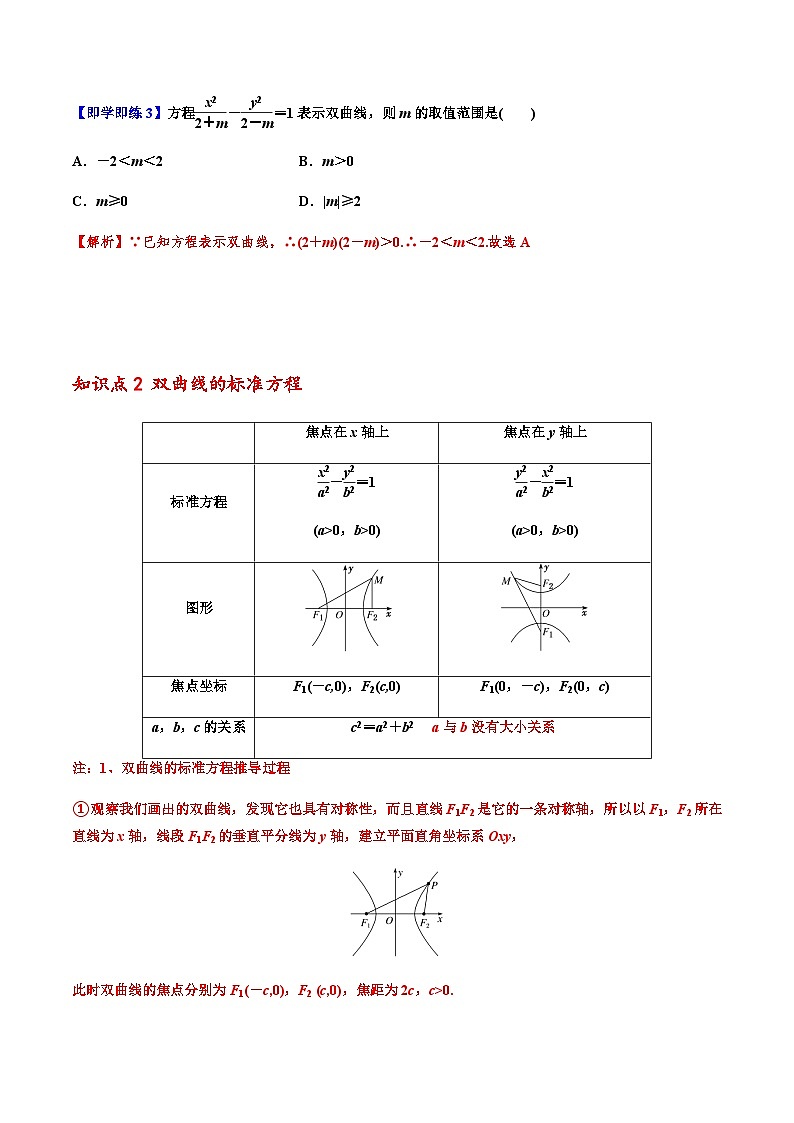
【即学即练3】方程-=1表示双曲线,则m的取值范围是( )
A.-2<m<2 B.m>0
C.m≥0 D.|m|≥2
知识点2 双曲线的标准方程
焦点在x轴上
焦点在y轴上
标准方程
-=1
(a>0,b>0)
-=1
(a>0,b>0)
图形
焦点坐标
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a,b,c的关系
c2=a2+b2 a与b没有大小关系
注:1、双曲线的标准方程推导过程
①观察我们画出的双曲线,发现它也具有对称性,而且直线F1F2是它的一条对称轴,所以以F1,F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系Oxy,
此时双曲线的焦点分别为F1(-c,0),F2 (c,0),焦距为2c,c>0.
设P(x,y)是双曲线上一点,则
||PF1|-|PF2||=2a(a为大于0的常数),
因为|PF1|=,|PF2|=,
所以-=±2a,①
类比椭圆标准方程的化简过程,化简①,得(c2-a2)x2-a2y2=a2(c2-a2),两边同除以a2(c2-a2),得-=1.
由双曲线的定义知,2c>2a,即c>a,所以c2-a2>0,类比椭圆标准方程的建立过程,令b2=c2-a2,其中b>0,代入上式,得-=1(a>0,b>0).
②设双曲线的焦点为 F1和F2,焦距为2c,而且双曲线上的动点P满足||PF1|-|PF2||=2a,其中c>a>0 ,以F1,F2所在直线为y轴,线段F1F2的垂直平分线为x轴,建立平面直角坐标系,如图所示,此时,双曲线的标准方程是什么?
【答案】-=1(a>0,b>0).
2、巧记双曲线焦点位置与方程的关系
两种双曲线 , ()的相同点是:它们的形状、大小都相同,都有,;不同点是:两种双曲线的位置不同,它们的焦点坐标也不同.
焦点跟着正项走,即若x2项的系数为正,则焦点在x轴上;若y2项的系数为正,则焦点在y轴上.
3、共焦点双曲线的设法
与双曲线-=1(a>0,b>0)有公共焦点的双曲线方程为-=1(-a2<λ
【即学即练4】以椭圆+=1长轴的端点为焦点,且经过点(3,)的双曲线的标准方程为________.
【即学即练5】求过点P,Q且焦点在坐标轴上的双曲线的标准方程.
【即学即练6】求以椭圆+=1的短轴的两个端点为焦点,且过点A(4,-5)的双曲线的标准方程.
【即学即练7】椭圆+=1与双曲线-=1有相同的焦点,则a的值是( )
A. B.1或-2
C.1或 D.1
知识点3 双曲线的焦点三角形
双曲线上的一点与两焦点所构成的三角形称为焦点三角形.解决焦点三角形问题常利用双曲线的定义和正弦定理、余弦定理.
以双曲线上一点P(x0,y0)(y0≠0)和焦点F1(-c,0),F2(c,0)为顶点的△PF1F2中,若∠F1PF2=θ,则
(1)双曲线的定义:
(2)余弦定理:=|PF1|2+|PF2|2-2|PF1||PF2|·cos θ.
(3)面积公式:S△PF1F2=|PF1||PF2|·sin θ,
重要结论:S△PF1F2=
推导过程:由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|·cos θ得
由三角形的面积公式可得
S△PF1F2=
=
【即学即练8】设F1,F2分别是双曲线x2-=1的左、右焦点,若点P在双曲线上,且|PF1|=5,则|PF2|=( )
A.5 B.3
C.7 D.3或7
【即学即练9】已知双曲线-=1的左、右焦点分别是F1,F2.若双曲线上一点P使得∠F1PF2=60°,求△F1PF2的面积.
【即学即练10】设F1,F2分别是双曲线x2-=1的左、右焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于( )
A.4 B.8 C.24 D.48
考点一 双曲线标准方程的认识
解题方略:
双曲线方程的辨识方法
将双曲线的方程化为标准方程的形式,假如双曲线的方程为+=1,则当mn<0时,方程表示双曲线.若则方程表示焦点在x轴上的双曲线;若则方程表示焦点在y轴上的双曲线.
【例1-1】“k<2”是“方程表示双曲线”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
变式1:已知方程+=1表示双曲线,则m的取值范围是( )
A.(-1,+∞) B.(2,+∞)
C.(-∞,-1)∪(2,+∞) D.(-1,2)
变式2:已知方程-=1表示双曲线,且该双曲线两焦点的距离为4,则n的取值范围是( )
A.(-1,3) B.(-1,)
C.(0,3) D.(0,)
变式3:在方程mx2-my2=n中,若mn<0,则方程所表示的曲线是( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的双曲线 D.焦点在y轴上的椭圆
【例1-2】已知双曲线+=1,焦点在y轴上,若焦距为4,则a等于( )
A. B.5
C.7 D.
考点二 求双曲线的标准方程
解题方略:
1.求双曲线标准方程的步骤
(1)定位:是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
(2)定量:是指确定a2,b2的数值,常由条件列方程组求解.
2.双曲线标准方程的两种求法
(1)定义法:根据双曲线的定义得到相应的a,b,c,再写出双曲线的标准方程.
(2)待定系数法:先设出双曲线的标准方程-=1或-=1(a,b均为正数),然后根据条件求出待定的系数代入方程即可.
注:若焦点的位置不明确,应注意分类讨论,也可以设双曲线方程为mx2+ny2=1的形式,注意标明条件mn<0.
【例2-1】求适合下列条件的双曲线的标准方程.
(1)a=3,c=4;
(2)焦点为(0,-6),(0,6),经过点A(-5,6).
变式1:根据下列条件,求双曲线的标准方程.
(1)与双曲线-=1有公共焦点,且过点(3,2);
(2)双曲线过两点P,Q.
变式2:已知双曲线的中心在坐标原点,且一个焦点为F1(-,0),点P在该双曲线上,线段PF1的中点坐标为(0,2),则该双曲线的标准方程为( )
A.-y2=1 B.x2-=1
C.-=1 D.-=1
变式3:设F1,F2是双曲线-y2=1的两个焦点,点P在双曲线上,当△F1PF2的面积为2时,·的值为( )
A.2 B.3
C.4 D.6
考点三 双曲线的焦点三角形
解题方略:
在解决双曲线中与焦点有关的问题时,要注意定义中的条件||PF1|-|PF2||=2a的应用;与三角形有关的问题要考虑正、余弦定理、勾股定理等.另外在运算中要注意一些变形技巧和整体代换思想的应用.
【例3-1】如图,若F1,F2是双曲线-=1的两个焦点.
(1)若双曲线上一点P到它的一个焦点的距离等于16,求点P到另一个焦点的距离;
(2)若P是双曲线左支上的点,且|PF1|·|PF2|=32,试求△F1PF2的面积.
变式1:已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=( )
A.2 B.4
C.6 D.8
变式2:设点P在双曲线-=1上,F1,F2为双曲线的两个焦点,且|PF1|∶|PF2|=1∶3,则△F1PF2的周长等于________.cos∠F1PF2=________.
变式3:已知双曲线-=1(a>0,b>0),F1,F2为其两个焦点,若过焦点F1的直线与双曲线的同一支相交,且所得弦长|AB|=m,则△ABF2的周长为( )
A.4a B.4a-m
C.4a+2m D.4a-2m
变式4:如图所示,已知双曲线-=1(a>0,b>0)中,c=2a,F1,F2为左、右焦点,P为双曲线上的点,∠F1PF2=60°,=12,求双曲线的标准方程.
变式5:已知点为双曲线的左焦点,过原点的直线l与双曲线C相交于P,Q两点.若,则______.
考点四 双曲线定义的应用
解题方略:
求解与双曲线有关的长度和最值问题,都可以通过相应的双曲线的定义去解决
【例4-1】已知A(-4,0),B是圆(x-1)2+(y-4)2=1上的点,点P在双曲线-=1的右支上,则|PA|+|PB|的最小值为( )
A.9 B.2+6
C.10 D.12
变式1:已知定点A(3,1),F是双曲线-=1的右焦点,P是双曲线右支上的动点,则|PA|+|PF|的最小值为( )
A. B.5+4 C.5-4 D.+4
变式2:如图,双曲线C:-=1的左焦点为F1,双曲线上的点P1与P2关于y轴对称,则|P2F1|-|P1F1|的值是( )
A.3 B.4 C.6 D.8
变式3:已知点P在曲线C1:-=1的右支上,点Q在曲线C2:(x+5)2+y2=1上,点R在曲线C3:(x-5)2+y2=1上,则|PQ|-|PR|的最大值是( )
A.6 B.8 C.10 D.12
考点五 双曲线的轨迹方程
【例5-1】设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )
A.-=1 B.-=1
C.-=1(x≤-3) D.-=1(x≥3)
变式1:已知点P(x,y)的坐标满足-=±,则动点P的轨迹是( )
A.椭圆 B.双曲线
C.两条射线 D.双曲线的一支
【例5-2】已知定点A(0,7),B(0,-7),C(12,2),以C为一个焦点作过A,B的椭圆,则另一个焦点F的轨迹是________________________.
【例5-3】动圆与圆x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹是( )
A.双曲线的一支 B.圆
C.椭圆 D.双曲线
变式1:已知动圆过定点,且与圆相外切,求动圆圆心的轨迹方程.
【例5-4】在中,,,直线,的斜率之积为求顶点的轨迹方程.
考点六 双曲线的实际应用
解题方略:
1、双曲线在实际生活中有着广泛的应用,解答该类问题的关键是从实际问题中挖掘出所有相关条件,将实际问题转化为求双曲线的标准方程的问题.
2、利用双曲线解决实际问题的基本步骤如下:
(1)建立适当的坐标系.
(2)求出双曲线的标准方程.
(3)根据双曲线的方程及定义解决实际应用问题(注意实际意义).
【例6-1】A,B,C是我方三个炮兵阵地,A在B正东6千米,C在B北偏西30°,相距4千米,P为敌炮阵地,某时刻A处发现敌炮阵地的某种信号,由于B,C两地比A距P地远.因此4 s后,B,C才同时发现这一信号,此信号的传播速度为1 km/s,A若炮击P地,求炮击的方向角.
变式1:某工程需要开挖一个横截面为半圆的柱形隧道,挖出的土只能沿道路AP,BP运到P处(如图),|AP|=100 m,|BP|=150 m,∠APB=60°,试说明怎样运土才能最省工.
题组A 基础过关练
1、已知F1(-8,3),F2(2,3),动点P满足|PF1|-|PF2|=10,则P点的轨迹是( )
A.双曲线 B.双曲线的一支
C.直线 D.一条射线
2、求适合下列条件的双曲线的标准方程:
(1)a=2,经过点A(2,-5),焦点在y轴上;
(2)与椭圆+=1有共同的焦点,它们的一个交点的纵坐标为4.
3、焦点在x轴上的双曲线经过点P(4,-3),且Q(0,5)与两焦点的连线互相垂直,则此双曲线的标准方程为________.
4、下列选项中的曲线与-=1共焦点的双曲线是( )
A.-=2 B.-=1
C.-=1 D.-=1
5、设m是常数,若点F(0,5)是双曲线-=1的一个焦点,则m=________.
6、动圆与圆x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹是( )
A.双曲线的一支 B.圆
C.椭圆 D.双曲线
7、【多选】已知方程+=1表示的曲线为C.给出以下四个判断正确的是( )
A.当1
C.若曲线C表示焦点在x轴上的椭圆,则1
8、如图所示,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且双曲线过C,D两顶点.若AB=4,BC=3,则此双曲线的标准方程为____________.
9、已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2.若双曲线上存在点A使得∠F1AF2=90°,且|AF1|=2|AF2|=4,则双曲线的方程为( )
A.x2-=1 B.-y2=1
C.-=1 D.-=1
题组B 能力提升练
10、已知方程-=1对应的图形是双曲线,那么k的取值范围是( )
A.k>5 B.k>5或-2
11、【多选】已知点P在双曲线C:-=1上,F1,F2是双曲线C的左、右焦点,若△PF1F2的面积为20,则下列说法正确的有( )
A.点P到x轴的距离为
B.|PF1|+|PF2|=
C.△PF1F2为钝角三角形
D.∠F1PF2=
12、设F1,F2分别是双曲线x2-=1的左、右焦点.若P在双曲线上,且·=0,则|+|的值为________.
13、已知P为双曲线-=1右支上一点,F1,F2分别为双曲线的左、右焦点,M为△PF1F2的内心.若,则△MF1F2的面积为( )
A.2 B.10 C.8 D.6
14、在周长为48的Rt△MPN中,∠MPN=90°,tan∠PMN=,求以M,N为焦点,且过点P的双曲线方程.
15、如图,B地在A地的正东方向4 km处,C地在B地的北偏东30°方向2 km处,河流的沿岸PQ(曲线)上任意一点D到A的距离比到B的距离远2 km,则曲线PQ的轨迹方程是________;现要在曲线PQ上选一处M建一座码头,向B,C两地转运货物,那么这两条公路MB,MC的路程之和最短是______km.
16、已知双曲线C:-=1(a>0,b>0)的焦点分别为F1(-5,0),F2(5,0),P为C上一点,PF1⊥PF2,tan∠PF1F2=,则C的方程为( )
A.x2-=1 B.-y2=1
C.-=1 D.-=1
17、已知双曲线的两个焦点为F1(-,0),F2(,0),M是此双曲线上的一点,且满足1·
2=0,|1|·|2|=2,则该双曲线的方程是( )
A.-y2=1 B.x2-=1
C.-=1 D.-=1
18、在△ABC中,已知|AB|=4,内角A,B,C满足2sin A+sin C=2sin B,建立适当的平面直角坐标系,求顶点C的轨迹方程.
题组C 培优拔尖练
19、如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.建立适当的平面直角坐标系,求曲线C的方程.
20、已知双曲线-=1的左、右焦点分别为F1,F2.
(1)若点M在双曲线上,且·=0,求M点到x轴的距离;
(2)若双曲线C与已知双曲线有相同焦点,且过点(3,2),求双曲线C的方程.
21、2008年5月12日,四川汶川发生里氏8.0级地震,为了援救灾民,某部队在如图所示的P处空降了一批救灾药品,要把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,若PA=100 km,PB=150 km,BC=60 km,∠APB=60°,试在灾民区中确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.
人教A版 (2019)选择性必修 第一册第三章 圆锥曲线的方程3.2 双曲线优秀课堂检测: 这是一份人教A版 (2019)选择性必修 第一册第三章 圆锥曲线的方程3.2 双曲线优秀课堂检测,文件包含321双曲线及其标准方程解析版docx、321双曲线及其标准方程原卷版docx等2份试卷配套教学资源,其中试卷共87页, 欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线精品同步达标检测题: 这是一份高中数学人教A版 (2019)选择性必修 第一册3.2 双曲线精品同步达标检测题,文件包含321双曲线及其标准方程-2023-2024学年高二数学考点讲解练人教A版2019选择性必修第一册解析版docx、321双曲线及其标准方程-2023-2024学年高二数学考点讲解练人教A版2019选择性必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共45页, 欢迎下载使用。
人教A版 (2019)选择性必修 第一册3.2 双曲线精品课后作业题: 这是一份人教A版 (2019)选择性必修 第一册3.2 双曲线精品课后作业题,共7页。













