


初中数学湘教版九年级上册5.2 统计的简单应用完整版ppt课件
展开在日常生活中,我们经常遇到各种各样的“率”:一个国家的森林覆盖率、一个省的婴儿出生率、一个电视栏目的收视率、一种产品的合格率等等.从统计的观点看,一个“率”就是总体中具有某些特性的个体在总体中所占的百分比.在一般情况下,当要考察的总体所含个体数量较多时,“率”的计算就比较复杂,有什么方法来对“率”作出合理的估计吗?
某工厂生产了一批产品,从中随机抽取1000件来检查,发现有10件次品.试估计这批产品的次品率.
总体中每一件产品都有相同的机会被抽取.
答:估计这批产品的次品率为1%.
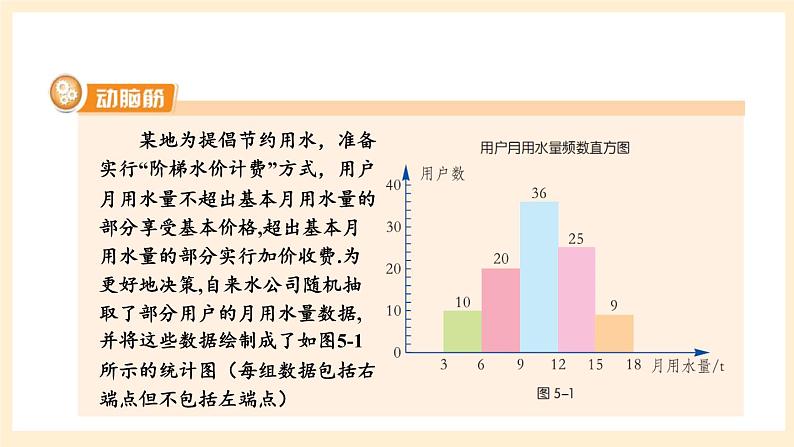
某地为提倡节约用水,准备实行“阶梯水价计费”方式,用户月用水量不超出基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取了部分用户的月用水量数据,并将这些数据绘制成了如图5-1所示的统计图(每组数据包括右端点但不包括左端点)
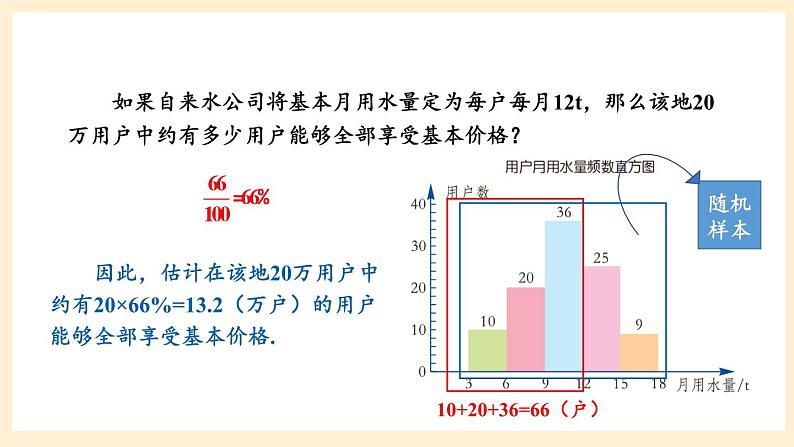
如果自来水公司将基本月用水量定为每户每月12t,那么该地20万用户中约有多少用户能够全部享受基本价格?
10+20+36=66(户)
因此,估计在该地20万用户中约有20×66%=13.2(万户)的用户能够全部享受基本价格.
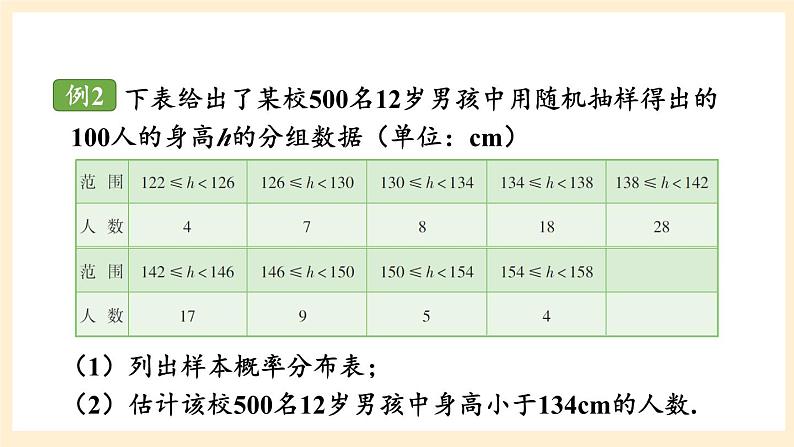
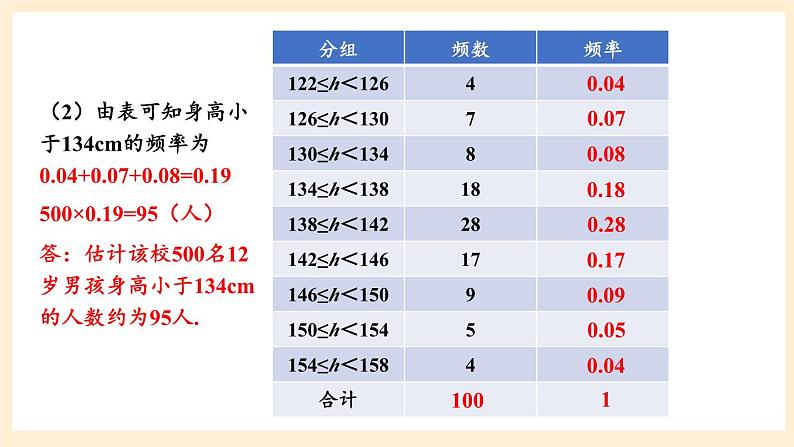
下表给出了某校500名12岁男孩中用随机抽样得出的100人的身高h的分组数据(单位:cm)
(1)列出样本概率分布表;(2)估计该校500名12岁男孩中身高小于134cm的人数.
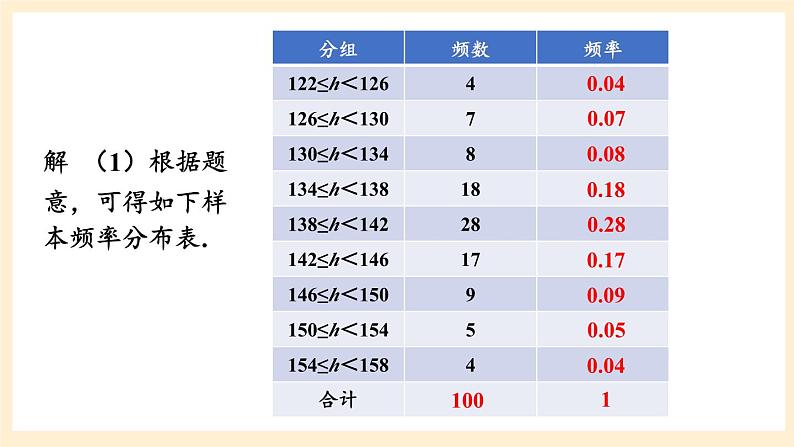
解 (1)根据题意,可得如下样本频率分布表.
(2)由表可知身高小于134cm的频率为0.04+0.07+0.08=0.19
500×0.19=95(人)
答:估计该校500名12岁男孩身高小于134cm的人数约为95人.
1.某市教育局为了解该市5万名九年级学生的身体素质情况,随机抽取了1000名九年级学生进行检测.已知被检测学生的身体素质达标率为95%,请据此估计该市九年级学生中身体素质达标的学生人数.
1000名学生是随机抽取的,所以1000名学生的身体素质是随机样本,因而可以用这个达标率(95%)作为该市九年级学生身体素质达标率的估计.
50000×95%=47500(人)
答:估计该市九年级学生身体素质达标人数为47500人.
2.为了让学生了解环保知识,增强环保意识,某市在中学生中举行了一次“环保知识竞赛”,共有19000名中学生参加了这次竞赛.为了解本次竞赛成绩情况,从中随机抽取了500名学生的成绩x(得分均为整数,满分为100分)进行统计后得到下表.请根据表格解答下列问题:(1)补全表格;(2)假设成绩在71分至90分之间(含71分,90分)的学生为二等奖,请据此估计该市获得二等奖的学生人数.
0.2+0.32=0.52
19000×0.52=9880(人)
答:估计该市获得二等奖的学生人数是9880人.
3.某灯具厂从1万件同批次产品中随机抽取了100件进行质检,发现其中有5件不合格,估计该厂这一万件产品中不合格品约为多少件?
解:∵某灯具厂从1万件同批次产品中随机抽取了100件进行质检,发现其中有5件不合格, ∴不合格率为:5÷100=5%, ∴估计该厂这一万件产品中不合格品为10000×5%=500件.
4.为了了解我市某县参加2008年初中毕业会考的6000名考生的数学成绩,从中抽查了200名学生的数学成绩(成绩为整数,满分120分)进行统计分析,并根据抽查结果绘制了如下的统计表和扇形统计图:
(1)请将以上统计表和扇形统计图补充完整;(2)若规定60分以下(不含60分)为“不合格”,60分以上(含60分)为“合格”,80分以上(含80分)为“优秀”,试求该样本的合格率、优秀率;(3)在(2)的规定下,请用上述样本的有关信息估计该县本次毕业会考中数学成绩优秀的人数和不合格的人数.
解:(1)79.5~89.5的人数是14%×200=28, 89.5~99.5的人数是11%×200=22, 69.5~79.5所占的百分比=46÷200×100%=23%; 59.5以下所占的百分比=28÷200×100%=14%; (2)合格率:1-14%=86%, 优秀率:14%+11%+16%=41%;(3)优秀人数:41%×6000=2460,不合格人数:14%×6000=840.
5. 2014年我市体卫站对某校九年级学生体育测试情况进行调研,从该校360名九年级学生中抽取了部分学生的成绩(成绩分为A、B、C三个层次)进行分析,绘制了频数分布表(如下),请根据图表信息解答下列问题:
(1)补全频数分布表; (2)如果成绩为A等级的同学属于优秀,请你估计该校九年级约有多少人达到优秀水平.
解:(1) (2)A等级的同学人数为40人,频率为0.40,∴估计该校九年级约有 0.4×360=144人达到优秀水平.
湘教版九年级上册5.2 统计的简单应用一等奖ppt课件: 这是一份湘教版九年级上册5.2 统计的简单应用一等奖ppt课件,文件包含522统计的简单应用2-课件pptx、522统计的简单应用2-试卷docx、522统计的简单应用2-教学设计docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
湘教版九年级上册5.2 统计的简单应用教学课件ppt: 这是一份湘教版九年级上册5.2 统计的简单应用教学课件ppt,文件包含湘教版数学九年级上册521用样本的“率”去估计总体相应的“率”pptx、第1课时用样本的“率”去估计总体相应的“率”doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
湘教版九年级上册5.2 统计的简单应用习题ppt课件: 这是一份湘教版九年级上册5.2 统计的简单应用习题ppt课件,共22页。PPT课件主要包含了发展趋势等内容,欢迎下载使用。













