第6章 图形的初步认识 知识梳理（一）-浙教版七年级数学上册章节复习

线段、射线和直线知识梳理

一、几何图形

1.定义：点、线、面、体称为几何图形.这些基本图形可帮助人们有效地刻画错综复杂的现实世界.

2.图形所表示的各个部分不在同一个平面内，这样的图形称为立体图形.如长方体，圆柱，圆锥等.

3.图形所表示的各个部分都在同一个平面内，这样的图形称为平面图形.如三角形，四边形，圆等.

二、线段，射线和直线

（一）直线

1.直线是从客观事物中抽象出来的，直线没有尽头，是向两边无限延长的.

2.直线的表示方法

（1）可以用这条直线上的两个点两个点来表示，如图所示的直线可以记作“直线AB”或“直线BA”，其中A、B为直线上任意的两个点.

（2）也可以用一个小写字母来表示，如图所示的直线可以记作“直线l”.

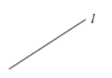
3.点与直线的关系

点P在直线l上，也可以说直线l经过点A；点M不在直线AB上，也可以说直线AB不经过点M.

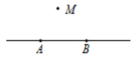
4.交点：当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点就是它们的交点.如直线a与直线b相交于点O.

5.直线的基本事实：经过两点有且只有一条直线，简单说成：两点确定一条直线.

【注】①直线无粗细、没有端点、向两方无限延伸，不能度量.

      ②平面上的两条直线，有相交和不想交两种位置关系.

（二）射线

1.   直线上的一点和它一旁的部分叫做线段，它是向一端无限延伸的.
2.   射线的表示方法

（1）可以用端点字母和另一个大写字母表示，如图可以记作“射线OA”，但不能写成“射线AO”.

（2）可以用一个小写字母来表示，如图可以记作“射线l”

【注】①射线是直线的一部分.

      ②射线向一方无限延伸，有一个端点，不能度量，不能比较大小.

      ③表示射线时，一定要把表示端点的字母写在前面.

（三）线段

1.   直线上两点和它们之间的部分叫做线段，这两个点叫做线段的端点.
2.   线段的表示方法

（1）用两个端点字母表示.如图可以记作“线段AB”或“线段BA”.

（2）用一个小写字母表示.如图可以记作“线段l” .

3.   延长线：线段的延长线即线段向一方延伸的部分.

如图1，延长AB是按B到A的方向延长；如图2，延长BA是按B到A的方向延长（或说成反向延长AB）.

4.   线段长度

连接两点间的线段的长度，叫做两点间的距离，它们是指线段的长度，是数量而不是线段本身.

5.   线段的基本事实

两点的所有连线中，线段最短.简单说成：两点之间，线段最短.

【注意】①线段是直线（或射线）的一部分.

        ②线段不能向两方无限延伸，可度量.

        ③线段有长短，但线段没有方向，表示线段的两个大写字母没有顺序.

（四）直线、射线和线段的区别与联系

三、计数问题

1.直线交点的个数

（1）两条直线相交，最多有1个交点；

（2）三条直线相交，最多有3个交点；

（3）四条直线相交，最多有6个交点；

那么20条直线相交，最多有几个交点呢？n条直线相交最多又有几个交点呢？

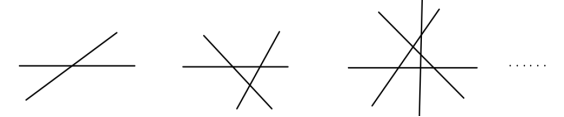
【结论】两条不重合的直线直线最多只有一个交点，n条直线最多有个交点.

2.线段的计数问题

【问题】数一数：图中一共有几条线段？

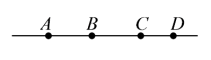
【提示】数线段需要掌握一定的方法和规律，必须要做到不重不漏.

【方法】一般方法是从左边第一个点起，使第一个点和其右边的每一个点各组合一次，得到（n-1）条线段，然后再从左边第二点起，使其和其右边的每个点各组合一次，又得到（n-2）条线段，...，依次数下去，最后进行相加.

【结论】若一条直线上有n个点，则线段的条数为.

四、线段和差

（一）线段的长短比较

1.尺规作图：仅用圆规和没有刻度的直尺作图的方法叫做尺规作图．

2.线段中点：把线段分成两条相等的线段的点叫做这条线段的中点.

3.用尺规作线段或比较线段

（1） 作一条线段等于已知线段：用圆规作一条线段等于已知线段．例如：下图所示，用圆规在射线AC上截取AB＝a．

（2）线段的比较：

①叠合比较法：利用直尺和圆规把线段放在同一条直线上，使其中一个端点重合，另一个端点位于重合端点同侧，根据另一端点与重合端点的远近来比较长短．如下图：

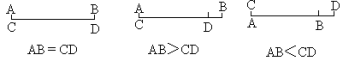
②线段的比较方法除了叠合比较法外，还可以用度量比较法．

4.线段和差

（1）一般地，如果一条线段的长度是另两条线段的长度的和，那么这条线段就叫做另两条线段的和；如果一条线段的长度是另两条线段的长度的差，那么这条线段就叫做另两条线段的差.两条线段的和或差仍是一条线段.

（2）解决线段计算问题的方法

①按照已知条件画出图形是正确解题的前提条件；注意分类讨论，多解问题.

②观察图形，找出线段之间的关系.

③简单问题可以通过列算式解决，复杂的问题可以设未知数，利用方程解决.

【注】直接用和差关系计算比较困难时，可引用方程思想；若没有指出具体图形的位置时，则需要进行分类讨论.