《三角形的三边关系》教学设计2-七年级下册数学北师大版

这是一份《三角形的三边关系》教学设计2-七年级下册数学北师大版，共4页。
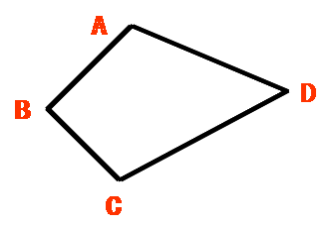
 【4.1.2 认识三角形】教学目标 :    1.认识等腰三角形，会将三角形按边进行分类。     2.掌握三角形三条边之间的关系。     3.能够熟练应用三角形的三边关系解决问题。教学重难点  重点：三角形三边之间的数量关系以及按边将三角形分类。     难点：灵活运用三角形三边关系解决一些实际问题。教学过程：一、【温故知新】A（1）由不在同一直线上的              条线段            相接所组成的 图形叫做                  .（2）三角形有     条边,      个内角,    个顶点.BC（3）“三角形” 用“    ”表示,如图三角形ABC    记作“                 ”.（4） 顶点 A 所对的边是        ，用边“      ”表示，或用“      ” 表示；顶点 B 所对的边是       ，用边“      ”表示，或用 “     ”表示；顶点 C 所对的边是         ，用边“       ”表示，或用“      ”表示。（5）按三角形内角的大小把三角形分为三类：                           （6）有两边相等的三角形叫          （7）有三边相等的三角形叫         二、【创设情境】用小棒摆三角形引入三角形三边关系 老师给同学们准备了一些小棒，同学们猜想一下，我们用任意三根一定能搭成三角形吗?  （展台展示）三、【合作探究】（结合课本85页）探索1：三角形的任意两边之和与第三边有何关系？ 完成课本【议一议】  猜想：   三角形的任意两边之和_____________第三边.  探究2：三角形的任意两边之差与第三边有何关系？ 完成课本【做一做】 猜想：    三角形的任意两边之差____________第三边. 【结论】  三角形任意两边之和___________第三边。三角形任意两边之差___________第三边。四、【课堂检测】1.任意三条线段都能组成三角形。(    )2.如果a+b>c ,那么a ,b ,c 三条线段可以构成三角形。（   ）3.若五条线段的长分别1cm, 2cm, 3cm, 4cm, 5cm, 则以其中三条线段为边可构成______个三角形。4. 若等腰三角形的两边长分别是3和4,则它的周长为           。若等腰三角形的两边长分别为3和7,则它的周长为_______; 5.已知两根木条长度分别为3cm和5cm ，要想拼成一个三角形，问第三根木条的长度a应取的范围______________。6.一个三角形的两边长分别为2cm和9cm，若第三边长为奇数，则第三边长为        。7.以下列各组线段为边，能组成三角形的是（  ）。A. 1cm,  2cm,  4cm    B. 8cm,  6cm,  4cm　　C. 12cm,  5cm,  6cm　  D. 2cm,  3cm,  6cm 五、【我学会了】1.三角形的三边关系：三角形任意两边之和大于第三边。三角形任意两边之差小于第三边。 2.判断三条线段能否组成三角形时，较为简便的判法：如果较短的两条边的和大于第三条边，就可以构成三角形，否则就不能。 3.确定第三边的取值范围：其余两边之  < 第三边 < 其余两边之  六、【拓展延伸】 1.若三角形ABC的三边分别为a, b, c,  则化简|a+b-c|-|b-a-c|的结果是______________。 2.某地有四个汽车停车场，位于如图所示的四边形ABCD的四个顶点，现在要建立一个汽车维修站，你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P，使点P到A，B，C，D四点的距离之和最小吗？