




还剩24页未读,
继续阅读
2023九年级数学下册第二十八章锐角三角函数小结课时2课件(人教版)
展开
这是一份2023九年级数学下册第二十八章锐角三角函数小结课时2课件(人教版),共32页。
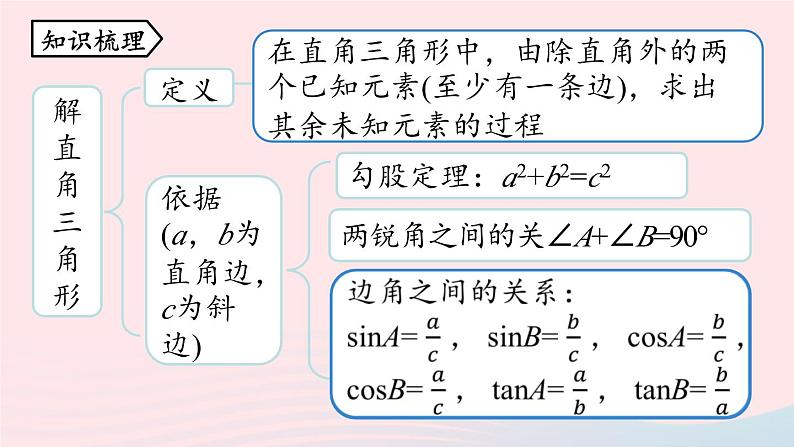
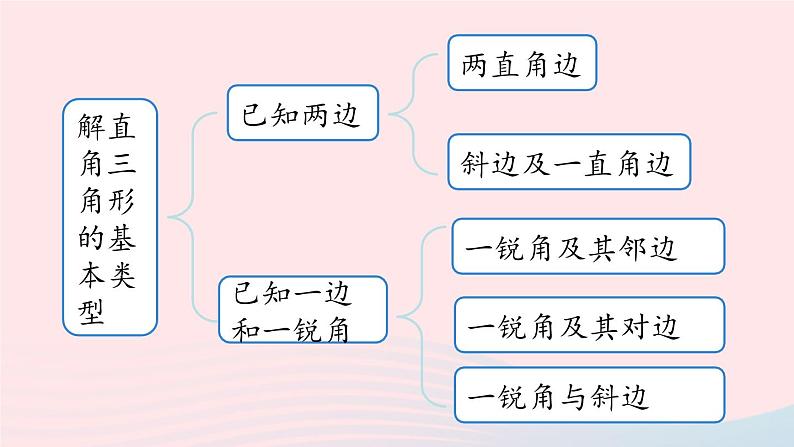
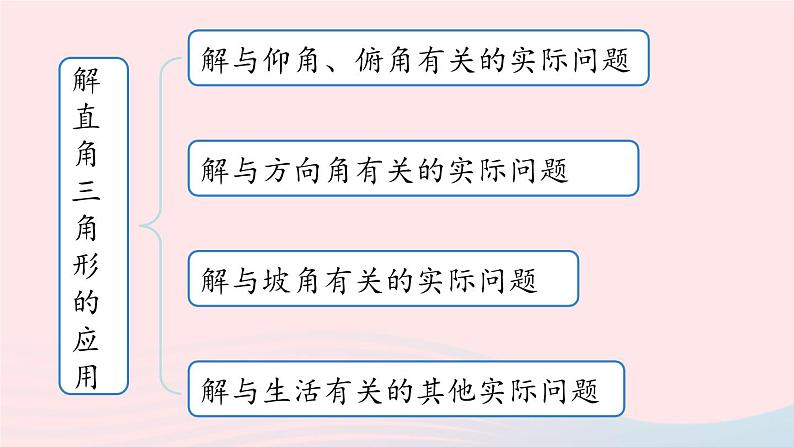
28 小结课九年级下册 RJ初中数学第2课时解直角三角形定义依据(a,b为直角边,c为斜边)勾股定理:a2+b2=c2两锐角之间的关∠A+∠B=90° 知识梳理解直角三角形的基本类型已知两边已知一边和一锐角两直角边斜边及一直角边一锐角及其邻边一锐角及其对边一锐角与斜边解直角三角形的应用解与仰角、俯角有关的实际问题解与方向角有关的实际问题解与坡角有关的实际问题解与生活有关的其他实际问题(1) 在Rt△ABC中,∠C=90°,a,b,c 分别是∠A,∠B,∠C 的对边.三边关系:___________;三角关系: ;边角关系:sinA=cosB=____ ,cosA=sinB = , tanA= ,tanB= .a2+b2=c2∠A=90°-∠B 5. 解直角三角形(2) 直角三角形可解的条件解直角三角形时知道其中的 2 个元素(至少有一个是边),就可以求出其余的 3 个未知元素.(3)直角三角形的解法①知一边一锐角:先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边,用正切求另一直角边,再用正弦或勾股定理求斜边;②知两边:先用勾股定理求另一边,再用边角关系求锐角;③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.(1) 仰角和俯角在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.6. 三角函数的应用仰角俯角以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方向角. 如图所示:(2) 方向角坡面与水平面的夹角叫做坡角,记作 α,有 i = tan α.坡度通常写成 1∶m 的形式,如 i =1∶6.显然,坡度越大,坡角 α 就越大,坡面就越陡.如图:坡面的铅垂高度(h)和水平长度(l)的比叫做坡度.记作 i,即 i = .(3) 坡度,坡角 1.将实际问题抽象为数学问题(画出平面图形, 转化为解直角三角形的问题); 2.根据条件的特点,适当选用锐角三角函数等 去解直角三角形; 3.得到数学问题的答案; 4.得到实际问题的答案.(4) 利用解直角三角形的知识解决实际问题的一般过程: 5k3k5k2k重点解析重难点4:解直角三角形 解:BC=BD+CD=4+6=10=AD, 2.已知:如图,Rt△AOB 中,∠O=90°,以 OA 为半径作⊙O,BC 切⊙O 于点 C,连接 AC 交 OB 于点 P.(1) 求证:BP=BC;解:连接OC.∵BC是⊙O的切线,∴∠OCB=90°,∴∠OCA+∠BCA=90°.∵OA=OC,∴∠OCA=∠OAC,∴∠OAC+∠BCA=90°,∵∠BOA=90°,∴∠OAC+∠APO=90°,∵∠APO=∠BPC,∴∠BPC=∠BCA,∴BP=BC. 注意:直径所对的圆周角为直角. E1.如图,防洪大堤的横截面是梯形 ABCD,其中 AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角 β=45°.若原坡长 AB =20 m,求改造后的坡长 AE.(结果保留根号) 重点解析重难点5:三角函数的应用 在 Rt△BDG 中,∵ BG=DG · tan30°, 解得 x ≈13,∴大树的高度约为 13 米.3.如图,轮船甲位于码头 O 的正西方向 A 处,轮船乙位于码头 O 的正北方向 C 处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为 45 km/h 和 36 km/h,经过 0.1 h,轮船甲行驶至 B 处,轮船乙行驶至 D 处,测得∠DBO=58°,此时 B 处距离码头 O 多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)解:设 B 处距离码头 O x km,在Rt△CAO 中, ∴CO=AO · tan∠CAO=(45×0.1+x)· tan45°=4.5+x,在Rt△DBO中, ∴DO=BO · tan∠DBO=x · tan58°,∵DC=DO-CO,∴36×0.1=x · tan58°-(4.5+x), 此时 B 处距离码头 O 约13.5 km. 深化练习 ∴ BC=BD+DC=5. 解:连接 BD.在⊙O 中,∠C =∠A,∵BF 是⊙O 的切线,∴∠ABF=90°.设 AB=4x,则 AF=5x,由勾股定理得,BF=3x.∵AB是⊙O 的直径,∴BD⊥AD, ∴△ABF∽△BDF, 解:作 DG⊥AB 于点 G,EH⊥AB 于点 H,则 GH=DE=2 米,EH=DG=10 米. 又∵AG=DG=10米, 4.如图,为了测出某塔 CD 的高度,在塔前的平地上选择一点 A,用测角仪测得塔顶 D 的仰角为30°,在A,C 之间选择一点 B(A,B,C 三点在同一直线上).用测角仪测得塔顶 D 的仰角为75°,且 AB 间的距离为 40 m. (1) 求点 B 到 AD 的距离; 75°30°ABC D (2) 求塔高CD (结果用根号表示). C
28 小结课九年级下册 RJ初中数学第2课时解直角三角形定义依据(a,b为直角边,c为斜边)勾股定理:a2+b2=c2两锐角之间的关∠A+∠B=90° 知识梳理解直角三角形的基本类型已知两边已知一边和一锐角两直角边斜边及一直角边一锐角及其邻边一锐角及其对边一锐角与斜边解直角三角形的应用解与仰角、俯角有关的实际问题解与方向角有关的实际问题解与坡角有关的实际问题解与生活有关的其他实际问题(1) 在Rt△ABC中,∠C=90°,a,b,c 分别是∠A,∠B,∠C 的对边.三边关系:___________;三角关系: ;边角关系:sinA=cosB=____ ,cosA=sinB = , tanA= ,tanB= .a2+b2=c2∠A=90°-∠B 5. 解直角三角形(2) 直角三角形可解的条件解直角三角形时知道其中的 2 个元素(至少有一个是边),就可以求出其余的 3 个未知元素.(3)直角三角形的解法①知一边一锐角:先由两锐角互余关系求出另一锐角;知斜边,再用正弦(或余弦)求另两边;知直角边,用正切求另一直角边,再用正弦或勾股定理求斜边;②知两边:先用勾股定理求另一边,再用边角关系求锐角;③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题.(1) 仰角和俯角在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.6. 三角函数的应用仰角俯角以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方向角. 如图所示:(2) 方向角坡面与水平面的夹角叫做坡角,记作 α,有 i = tan α.坡度通常写成 1∶m 的形式,如 i =1∶6.显然,坡度越大,坡角 α 就越大,坡面就越陡.如图:坡面的铅垂高度(h)和水平长度(l)的比叫做坡度.记作 i,即 i = .(3) 坡度,坡角 1.将实际问题抽象为数学问题(画出平面图形, 转化为解直角三角形的问题); 2.根据条件的特点,适当选用锐角三角函数等 去解直角三角形; 3.得到数学问题的答案; 4.得到实际问题的答案.(4) 利用解直角三角形的知识解决实际问题的一般过程: 5k3k5k2k重点解析重难点4:解直角三角形 解:BC=BD+CD=4+6=10=AD, 2.已知:如图,Rt△AOB 中,∠O=90°,以 OA 为半径作⊙O,BC 切⊙O 于点 C,连接 AC 交 OB 于点 P.(1) 求证:BP=BC;解:连接OC.∵BC是⊙O的切线,∴∠OCB=90°,∴∠OCA+∠BCA=90°.∵OA=OC,∴∠OCA=∠OAC,∴∠OAC+∠BCA=90°,∵∠BOA=90°,∴∠OAC+∠APO=90°,∵∠APO=∠BPC,∴∠BPC=∠BCA,∴BP=BC. 注意:直径所对的圆周角为直角. E1.如图,防洪大堤的横截面是梯形 ABCD,其中 AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角 β=45°.若原坡长 AB =20 m,求改造后的坡长 AE.(结果保留根号) 重点解析重难点5:三角函数的应用 在 Rt△BDG 中,∵ BG=DG · tan30°, 解得 x ≈13,∴大树的高度约为 13 米.3.如图,轮船甲位于码头 O 的正西方向 A 处,轮船乙位于码头 O 的正北方向 C 处,测得∠CAO=45°,轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为 45 km/h 和 36 km/h,经过 0.1 h,轮船甲行驶至 B 处,轮船乙行驶至 D 处,测得∠DBO=58°,此时 B 处距离码头 O 多远?(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)解:设 B 处距离码头 O x km,在Rt△CAO 中, ∴CO=AO · tan∠CAO=(45×0.1+x)· tan45°=4.5+x,在Rt△DBO中, ∴DO=BO · tan∠DBO=x · tan58°,∵DC=DO-CO,∴36×0.1=x · tan58°-(4.5+x), 此时 B 处距离码头 O 约13.5 km. 深化练习 ∴ BC=BD+DC=5. 解:连接 BD.在⊙O 中,∠C =∠A,∵BF 是⊙O 的切线,∴∠ABF=90°.设 AB=4x,则 AF=5x,由勾股定理得,BF=3x.∵AB是⊙O 的直径,∴BD⊥AD, ∴△ABF∽△BDF, 解:作 DG⊥AB 于点 G,EH⊥AB 于点 H,则 GH=DE=2 米,EH=DG=10 米. 又∵AG=DG=10米, 4.如图,为了测出某塔 CD 的高度,在塔前的平地上选择一点 A,用测角仪测得塔顶 D 的仰角为30°,在A,C 之间选择一点 B(A,B,C 三点在同一直线上).用测角仪测得塔顶 D 的仰角为75°,且 AB 间的距离为 40 m. (1) 求点 B 到 AD 的距离; 75°30°ABC D (2) 求塔高CD (结果用根号表示). C
相关资料
更多









