







28《数学活动》课件+导学案
展开数学活动
——利用测角仪测量物高
一、导学
1.活动导入
请同学们准备如下学具:半圆形量角器一个,细线一根,小挂件(或其他小重物),软尺一个.
这节课我们利用测角仪测量物高.
2.活动目标
(1)能自制测角仪,根据实际情况设计测量物高的方案.
(2)能运用解直角三角形的知识根据测量的数据计算物高.
3.活动重、难点
重点:自制测角仪,测量物高.
难点:测量活动.
二、活动过程
1.活动指导
(1)活动内容:教材P81活动1、2:制作测角仪,测量树的高度;利用测角仪测量塔高.
(2)活动时间:45分钟.
(3)活动方法:完成活动参考提纲.
(4)活动参考提纲:
①自制测角仪:
把一根细线固定在半圆形量角器的圆心处,细线的另一端系一个小挂件,如图1、2所示,制成的一个简单测角仪.
图1 图2 图3
②探索测角仪的使用方法:如图3所示,仰角的度数是多少?
③测量原理探讨:
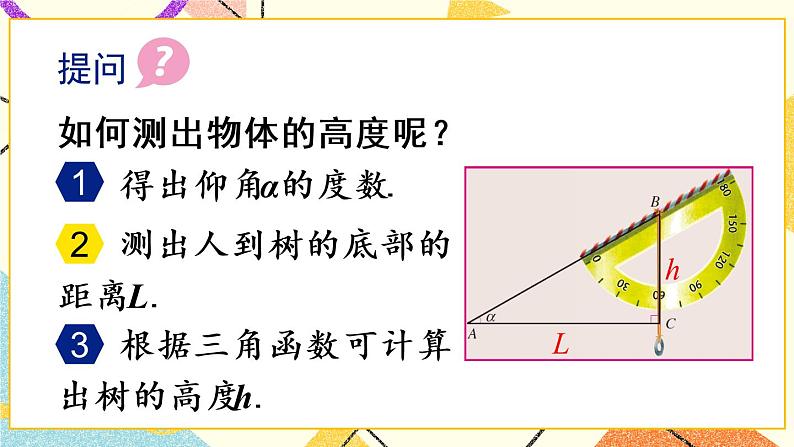
a.测量底部可以到达的物体的高度,如图4:
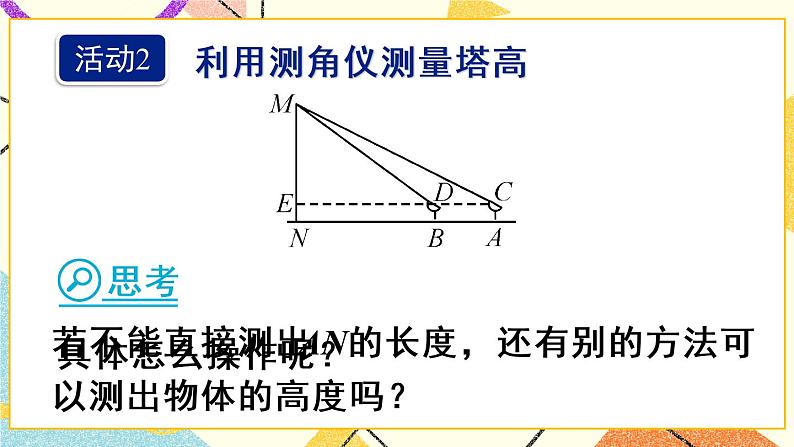
b.测量底部不可以直接到达的物体的高度,如图5:
④探讨测量方案,设计活动报告:
a.测量树高(底部可以到达的物高),如图6:
b.测量塔高(底部不可到达的物高),如图7:
图6 图7
⑤活动实施:
a.设计测量方案.
b.实际测量,记录数据.
c.整理数据计算物高.
d.填写活动报告.
课题 |
| |||
测量示意图 |
| |||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
|
|
|
| |
|
|
|
| |
|
|
|
| |
计算过程 |
| |||
结论 |
| |||
2.自学:学生参考活动指导进行活动性学习.
3.助学
(1)师助生:
①明了学情:了解学生是否能制作测角仪、设计测量方案,并积极参与活动.
②差异指导:全班学生每6人一组分组活动,指导学生制作测角仪、设计测量方案,督促学生认真完成活动.
(2)生助生:小组内互相交流.
4.强化
(1)底部可以到达的物高的测量原理.
(2)底部不可到达的物高的测量原理.
三、评价
1.学生学习的自我评价:这节课你有什么收获?有哪些不足?
2.教师对学生的评价:
(1)表现性评价:从学生参与活动的积极性、动手操作能力等方面进行评价.
(2)纸笔评价:活动报告评价检测.
3.教师的自我评价(教学反思).
本课时的数学活动是利用测角仪测量物高.整个活动过程应充分发挥学生的主动性,指导学生利用半圆形量角器、细线、小挂件制作一个简单的测角仪,对于在活动过程中有问题的学生及时给予帮助,增强与学生的互动和交流,将实际问题转化为数学模型,利用解直角三角形的知识进行解答.
一、基础巩固(60分)
1. (20分)某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动,如图是四个小组在不同位置测量后绘制的示意图,用测角仪测得旗杆顶端A的仰角记为α,CD为测角仪的高,测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB,四个小组测量和记录数据如下表所示:
(1)利用第四组学生测量的数据,求旗杆AB的高度(精确到0.1m);
(2)四组学生测量旗杆高度的平均值为 9.7 m(精确到0.1m).
2.(20分)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10 m到达B点,在B处测得树顶C的仰角为60°(A、B、D三点在同一直线上).请你根据他们的测量数据计算这棵树的高度(结果精确到0.1 m).
解:设CD=x.在Rt△BCD中,BD= .在Rt△ACD中,AD=.
∴AB=AD-BD,即=10,∴x=.
∴CD=≈8.7(m).
因此,这棵树的高度约为8.7 m.
3.(20分)如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆的高度.已知小明的眼睛与地面的距离(AB)是1.7 m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M的仰角为45°;小红眼睛与地面的距离(CD)是1.5 m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28 m且位于旗杆两侧(点B、N、D在同一条直线上).求旗杆MN的高度(结果精确到0.1 m).
解:如图所示,作AE⊥MN于E,CF⊥MN于F.设MN=x.
在Rt△MAE中,ME=MN-EN=MN-AB=x-1.7,∠MAE=45°,
∴AE=ME=x-1.7.
在Rt△MCF中,MF=MN-NF=MN-CD=x-1.5,∠MCF=30°,
∴FC=.
又∵BD=BN+ND=AE+FC,∴x-1.7+ (x-1.5)=28.
∴x≈11.8.∴MN≈11.8(m).
因此,旗杆MN的高度约为11.8 m.
二、综合应用(20分)
4.(20分)大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,求塔BC的高度.
解:作DE⊥BC于E.设BC=x,在Rt△ABC中,
.
在Rt△BDE中,BE=BC-EC=BC-AD=x-100,∠BDE=30°,
∴.
又∵DE=AC,∴x= (x-100),
∴x=150.∴BC=150(米).
因此,塔BC的高度为150米.
三、拓展延伸(20分)
5.(20分)某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动.他们在河边的一点A处测得河对岸小山顶上一座铁塔的塔顶C的仰角为60°、塔底B的仰角为45°,已知铁塔的高度BC为20 m(如图),你能根据以上数据求出小山的高BD吗?若不能,请说明理由;若能,请求出小山的高BD(精确到0.1 m).
解:能,过程如下:
设AD=x,在Rt△ABD中,∠BAD=45°,∴BD=AD=x.
在Rt△ACD中,∠CAD=60°,∴CD=AD·tan60°=3x.
又∵BC=CD-BD,∴x-x=20,∴x≈27.3.
∴BD≈27.3(m).
因此,小山的高BD约为27.3 m.









