高中3.3 抛物线作业课件ppt

这是一份高中3.3 抛物线作业课件ppt，共21页。

解析 抛物线方程化成标准方程形式为x2=8y,可得其开口向上,焦点坐标为(0,2),准线方程为y=-2.
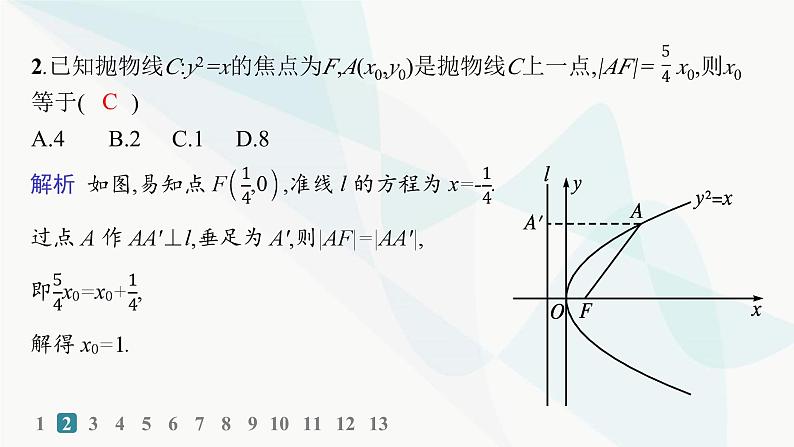
2.已知抛物线C:y2=x的焦点为F,A(x0,y0)是抛物线C上一点,|AF|= x0,则x0等于(　　)A.4B.2C.1D.8
3.如图,在正方体ABCD-A1B1C1D1中,P是平面BB1C1C内一动点,若点P到直线BC与直线C1D1的距离相等,则动点P的轨迹是(　　)A.直线B.圆C.双曲线D.抛物线
解析 由题意,知直线C1D1⊥平面BB1C1C,则C1D1⊥PC1,即|PC1|就是点P到直线C1D1的距离,那么点P到直线BC的距离等于它到点C1的距离,所以点P的轨迹是抛物线.
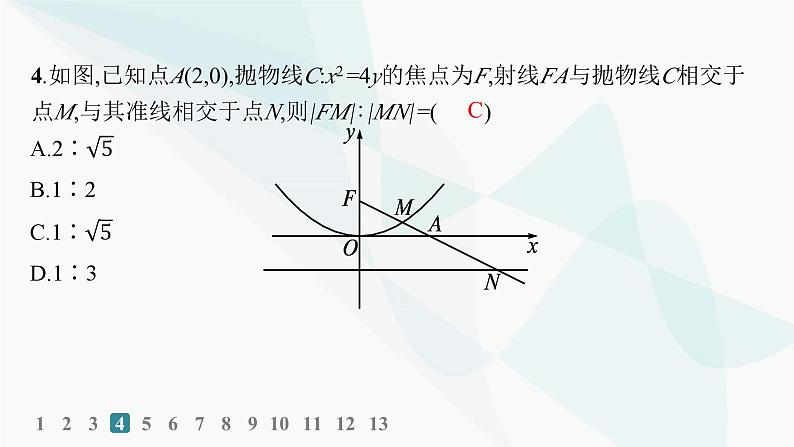
4.如图,已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|∶|MN|=(　　)
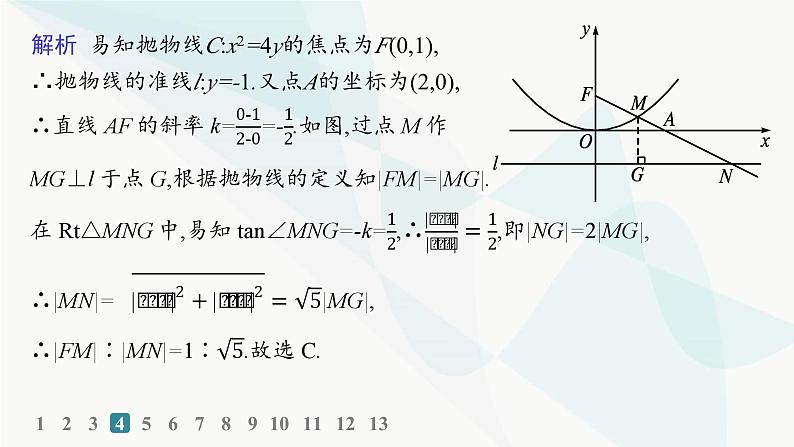
解析 易知抛物线C:x2=4y的焦点为F(0,1),∴抛物线的准线l:y=-1.又点A的坐标为(2,0),
解析 过点Q作QQ'⊥l于点Q',如图.∵ ,∴|PQ|∶|PF|=3∶4,又焦点F到准线l的距离为4,∴|QF|=|QQ'|=3.
6.在平面直角坐标系Oxy中,双曲线C: -y2=1的焦距为　　　;若双曲线C的右焦点与抛物线y2=2px(p>0)的焦点重合,则实数p的值为　　　. 
7.已知抛物线y2=4x上一点P到准线的距离为d1,到直线l:4x-3y+11=0的距离为d2,则d1+d2的最小值为　　　　　. 
解析 抛物线上的点P到准线的距离等于到焦点F的距离,所以过焦点F作直线4x-3y+11=0的垂线,则点F到直线4x-3y+11=0的距离为d1+d2的最小值,如图所示,故(d1+d2)min= =3.
8.若抛物线顶点在原点,对称轴是x轴,点P(-5,2 )到焦点的距离是6,求抛物线的标准方程.
解 设焦点为F(a,0),依题意有|PF|= =6,即a2+10a+9=0,解得a=-1或a=-9.当焦点为F(-1,0)时,抛物线开口方向向左,其方程为y2=-4x;当焦点为F(-9,0)时,抛物线开口方向向左,其方程为y2=-36x.综上,抛物线的标准方程为y2=-4x或y2=-36x.
9.如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为(　　)A.y2=9xB.y2=6xC.y2=3xD.y2= x
解析 如图,分别过点A,B作AA1⊥l于点A1,BB1⊥l于点B1,由抛物线的定义知,|AF|=|AA1|,|BF|=|BB1|.∵|BC|=2|BF|,∴|BC|=2|BB1|,∴∠BCB1=30°,∴∠AFx=60°.连接A1F,则△AA1F为等边三角形,过点F作FF1⊥AA1于点F1,则F1为AA1的中点.设l交x轴于点K,则∴抛物线方程为y2=3x.
10.已知P为抛物线x2=12y上一个动点,Q为圆(x-4)2+y2=1上一个动点,则点P到点Q的距离与点P到x轴距离之和的最小值是(　　)A.4B.3C.2D.1
解析 由抛物线的方程可知焦点F(0,3),则准线方程为y=-3,如图,过点P作x轴的垂线,垂足为点A,延长PA交准线于点B,设圆(x-4)2+y2=1的圆心为点C.根据抛物线的定义可得|PA|=|PB|-|AB|=|PF|-|AB|,∴|PA|+|PQ|=|PF|+|PQ|-|AB|=|PF|+|PQ|-3,∴当|PA|+|PQ|最小时,|PF|+|PQ|最小,即F,P,Q(Q位于C,P之间)三点共线时,|PA|+|PQ|最小,
11.在平面直角坐标系Oxy中,圆M:(x-1)2+y2=1,点A(3,1),P为抛物线y2=2x上任意一点(异于原点),过点P作圆M的切线PB,B为切点,则|PA|+|PB|的最小值是　　　　　　. 
解析 设点P(x,y),可得y2=2x,圆M:(x-1)2+y2=1的圆心M(1,0),半径为1,连接PM,如图所示,即|PB|等于点P到y轴的距离.过点A作y轴的垂线,垂足为K,可得A,P,K三点共线时,|PA|+|PB|取得最小值|AK|=3,故|PA|+|PB|的最小值为3.
12.设P是抛物线y2=4x上的一个动点,F为抛物线的焦点.(1)若点P到直线x=-1的距离为d,点A(-1,1),求|PA|+d的最小值;(2)若点B(3,2),求|PB|+|PF|的最小值.
解 (1)依题意,抛物线的焦点为F(1,0),准线方程为x=-1.由已知及抛物线的定义,可知|PF|=d,于是问题转化为求|PA|+|PF|的最小值.由平面几何知识,知当F,P,A三点共线且P位于A,F中间时,|PA|+|PF|取得最小值,最小值为|AF|= ,即|PA|+d的最小值为 .
过点B作BQ垂直准线于点Q,交抛物线于点P1(如图所示).由抛物线的定义,可知|P1Q|=|P1F|,则|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=3+1=4,所以|PB|+|PF|的最小值为4.
13.已知过抛物线y2=2px(p>0)的焦点,斜率为2 的直线交抛物线于A(x1,y1),B(x2,y2)(x1

相关课件

人教A版 (2019)3.3 抛物线集体备课ppt课件：

这是一份人教A版 (2019)3.3 抛物线集体备课ppt课件，共40页。PPT课件主要包含了目录索引，本节要点归纳等内容，欢迎下载使用。

高中数学人教A版 (2019)选择性必修 第一册3.1 椭圆作业ppt课件：

这是一份高中数学人教A版 (2019)选择性必修 第一册3.1 椭圆作业ppt课件，共28页。

数学1.2 空间向量基本定理作业课件ppt：

这是一份数学1.2 空间向量基本定理作业课件ppt，共24页。