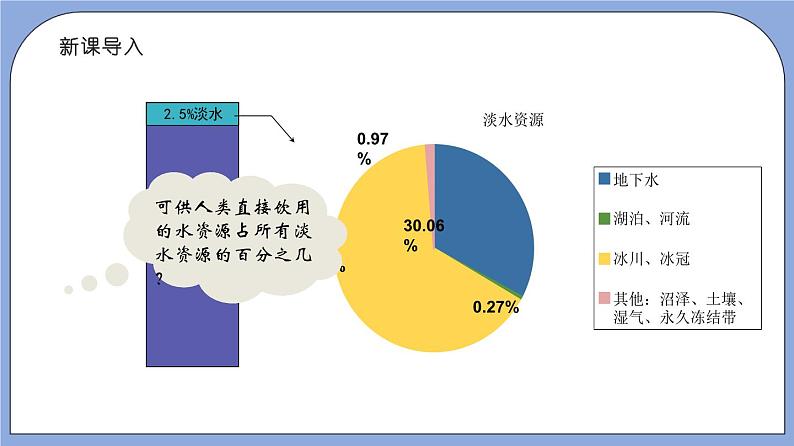
初中数学3.5 百分比的应用精品教学作业ppt课件

3.5百分比的应用—统计问题（第2课时）（作业）

一、单选题

1．（2020·全国·课时练习）观察七（1）班学生上学方式统计图，下列关于图中信息描述不正确的是（    ）

七（1）班学生上学方式统计图

A．该班骑车上学的人数不到全班人数的20%

B．该班步行上学人数超过骑车人数的50%

C．该班共有学生48人

D．该班乘车上学的学生人数超过半数

【答案】D

【分析】先根据统计图可分别得出步行、骑车、乘车、其他四种上学方式的学生人数，再据此求出相应的百分比，进行判断即可得．

【详解】由统计图得：步行、骑车、乘车、其他四种上学方式的学生人数依次为，

则该班骑车上学人数占全班人数的，选项A正确；

该班步行上学人数超过骑车人数的，选项B正确；

该班学生人数为（人），选项C正确；

该班乘车上学人数占全班人数的，即不超过半数，选项D不正确；

故选：D．

【点睛】本题考查了百分数的应用，读懂统计图，掌握百分数的求法是解题关键．

2．（2022·安徽·合肥市第四十五中学模拟预测）下面两图是某班全体学生上学时，乘车、步行、骑车的人数分布条形统计图和扇形统计图（两图均不完整），则下列结论中错误的是（    ）

A．该班总人数为50人 B．骑车人数占总人数的20%

C．乘车人数是骑车人数的倍 D．步行人数为30人

【答案】D

【分析】此题首先根据乘车人数和所占总数的比例，求出总人数，即可根据图中获取信息求出步行的人数；根据乘车和骑车所占比例，可得乘车人数是骑车人数的2.5倍．

【详解】根据条形图可知：

乘车的人数是25人，所以总数是：25÷50%=50(人)；故A选项正确；

骑车人数在扇形图中占总人数的：1-50%-30%=20%；故B选项正确；

则乘车人数是骑车人数的2.5倍；故C选项正确；

步行人数为30%×50=15(人)，故D选项错误；

故选：D．

【点睛】本题考查了扇形统计图和条形统计图及相关计算．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．

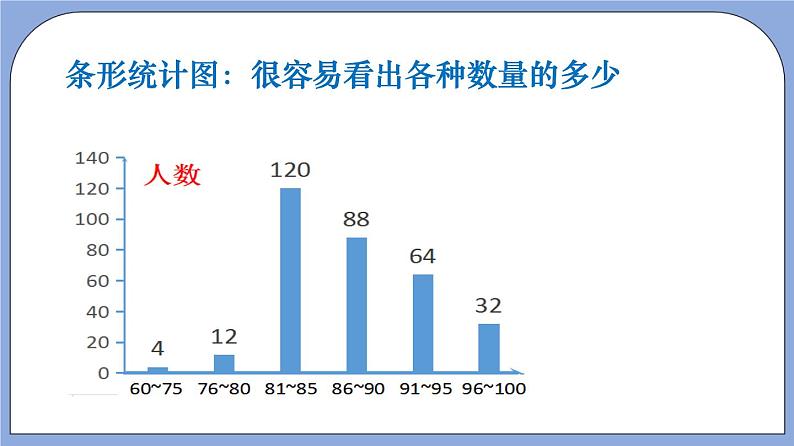
3．（2020·全国·课时练习）老师布置了10道作业题，学习委员将全班同学的答题情况绘制成条形图，根据统计图可知，答对8道题以上的同学占全班同学的百分数是（    ）

A．40% B．38% C．16% D．92%

【答案】C

【分析】根据条形统计图求出总共的人数，再求出答对8道题以上的同学人数，即可得出答案．

【详解】总共的人数有8+10+12+12+8=50人，

答对8道题以上的同学有8人，

∴答对8道题以上的同学占全班同学的百分数是：，

故选：C．

【点睛】本题主要考查了条形统计图的应用，利用条形图得出总人数与答对8道题以上的同学人数是解题关键．

二、填空题

4．（2020·上海市静安区实验中学课时练习）校兴趣小组共有50名队员，其中女队员20名，男队员人数占运动队总人数的百分率是_____．

【答案】60%

【分析】根据男队员÷总人数乘以100%计算即可；

【详解】男队员：50-20=30名，所以男队员人数占运动队总人数的百分率是．

【点睛】本题主要考查了概率的求解，准确计算是解题的关键．

5．（2018·上海普陀·期末）某班共50名学生，如果数学考试不及格的人数为5人，那么该班数学考试的及格率为_____．

【答案】90%

【详解】×100%=90%.

答：这次数学测验的及格率是90%.

故答案为90%.

6．（2021·上海市淞谊中学阶段练习）小明给小燕倒了一杯满满的橙汁，小燕先喝了这杯橙汁的20%，然后加满水，又喝了一杯的，再倒满水后又喝了半杯，然后又加满水，最后把一杯都喝了，小燕喝的橙汁和水的比是_____________．（用最简整数比表示）

【答案】10：11

【分析】设杯子的体积为毫升，用表示喝去橙汁的体积和水的体积，再计算其最简整数比．

【详解】解：设杯子的体积为毫升，则喝掉的橙汁体积为毫升，喝掉的水的体积为：（毫升），

∴小燕喝的橙汁和水的比是，

故答案为：10：11．

【点睛】本题考查了百分数，关键是正确地用x表示喝掉的水和橙汁的体积．

三、解答题

7．（2020·上海市静安区实验中学课时练习）六（1）班有40名学生，在数学测验中有38人及格，求这次测验的及格率．

【答案】这次测验的及格率

【分析】根据及格人数除以总人数乘以100%即可；

【详解】这次测验的及格率．

【点睛】本题主要考查了百分数的实际应用，准确计算是解题的关键．

8．（2021·上海松江·期末）某校六年级三个班共120名学生参加了数学小论文比赛，如图所示是各班参赛学生人数情况统计，请根据图上信息解答下列问题：

(1)六（1）班参赛人数占全部参赛人数的几分之几？

(2)如果六（2）班参赛人数与六（3）班参赛人数之比是3：5，那么六（3）班有多少人参赛？

(3)在（2）的条件下，六（1）班的获奖率为50%，六（1）班比六（2）班多了8人获奖，求六（2）班的获奖率．

【答案】(1)

(2)50人

(3)40%

【分析】（1）根据扇形统计图中六（1）班对应的圆心角度数，可以计算出六（1）班参赛人数占全部参赛人数的几分之几；

（2）根据六年级三个班共120名学生参加了数学小论文比赛和扇形统计图中的数据，可以计算出六（3）班有多少人参赛；

（3）根据题意和题目中的数据，可以计算出六（2）班的参赛学生数和获奖学生数，然后即可得到六（2）班的获奖率．

(1)

解： ，

即六（1）班参赛人数占全部参赛人数的；

(2)

解：120×（1﹣）×＝120×＝50（人），

即六（3）班有50人参赛；

(3)

解：由题意可得，六（1）班的获奖的获奖学生有：120××50%＝20（人），

∵六（1）班比六（2）班多了8人获奖，

∴六（2）班的获奖学生有：20﹣8＝12（人），

六（2）班的参赛学生学生有：120﹣120×﹣50＝30（人），

则六（2）班的获奖率是：×100%＝40%，

即六（2）班的获奖率为40%．

【点睛】本题考查扇形统计图，解答本题的关键是明确题意，利用扇形统计图的特点解答．

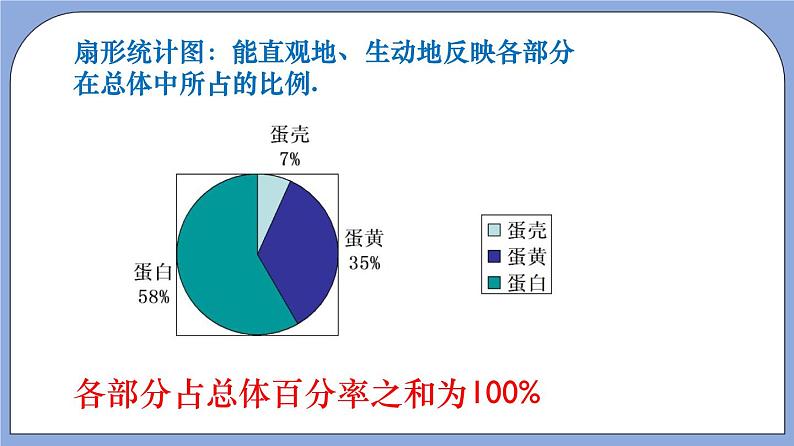
9．（2022·上海浦东新·期末）某园林单位对、、、四个品种共500株果树幼苗进行成活实验，先把这500株幼苗中各种幼苗所占百分比绘制成图1．其中、两种果树幼苗数量都为125株，种果树幼苗比种果树幼苗多20%．然后将这些幼苗进行成活实验，并将实验数据绘制成图2．

(1)种果树幼苗的数量为______株．

(2)在图1中，种果树幼苗区域的扇形圆心角度数为______度．

(3)、、、四个品种中，哪一个品种的成活率最高？请通过计算说明理由．

【答案】(1)150

(2)72

(3)品种的成活率最高，理由见解析

【分析】（1）根据种果树幼苗数量为125株，种果树幼苗比种果树幼苗多20%，即可求得种果树幼苗的数量；

（2）根据总数500减去种果树幼苗数量求得种果树幼苗数量，根据种果树幼苗数量除以总数500，乘以360°即可求得图1中，种果树幼苗区域的扇形圆心角度数；

（3）根据图2分别计算种果树幼苗的成活率，进而比较即可求解．

(1)

种果树幼苗的数量：（棵）

故答案为：150；

(2)

种果树幼苗的数量为：

种果树幼苗区域的扇形圆心角度数为：

故答案为：72

(3)

品种成活率：；    

品种成活率：；

品种成活率：；    

品种成活率：

答：品种的成活率最高．

【点睛】本题考查了扇形统计图，条形统计图，百分数的运算，根据题意求得种果树幼苗数量是解题的关键．

10．（2021·上海虹口·期末）学校的六年级同学举行“新冠肺炎”知识小竞赛．比赛结束后老师对成绩进行整理，并绘制出以下两幅未完成的统计图．请根据图1和图2提供的信息，回答下列问题：

(1)A学校六年级学生共         名；

(2)扇形统计图中“不合格”部分所占百分比为         ；“优秀”部分所对应的圆心角的度数为         度；

(3)B学校的六年级同学也参加了这次竞赛，其成绩如下表：

如果规定：优良率（优秀和良好占参赛总人数的百分率）高者为胜，那么哪一所学校在这次竞赛中得胜？请计算并说明理由．（在百分号前保留一位小数）

【答案】(1)100

(2)10%，126

(3)B校获胜，见解析

【分析】（1）由良好的人数及其所占百分比即可得出A学校六年级学生人数；

（2）用不合格人数除以被调查的总人数可得其对应百分比，用360°乘以“优秀”人数所占比例即可；

（3）分别求出A、B学校的优良率，比较大小即可得出答案．

(1)

A学校六年级学生共有45÷45%=100（名），

故答案为：100；

(2)

扇形统计图中“不合格”部分所占百分比为×100%=10%，

“优秀”部分所对应的圆心角的度数为n=360°×=126°，

故答案为：10%，126；

(3)

B校在这次竞赛中得胜，理由如下：

∵A学校的优良率为×100%=80%，B学校的优良率为×100%≈81.5%，

∴81.5%＞80%，

∴B学校在这次竞赛中得胜．

【点睛】本题考查条形统计图、扇形统计图，理解统计图中的数量和数量关系是正确计算的前提．

11．（2018·上海普陀·期末）为了解某中学六（1）班学生喜欢球类活动的情况，采取全面调查的方法（要求每位学生只能选择一种自己喜欢的球类），并绘制扇形统计图（如图所示），其中喜欢篮球的学生有12人，喜欢足球的学生有8人，请你根据图中提供的信息解答下列问题：

（1）求六（1）班喜欢乒乓球的人数；

（2）扇形统计图中m=_________，表示“排球”的扇形的圆心角是________度；

（3）学校要从六（1）班喜欢乒乓球的同学中随机选取2名学生参加学校的乒乓队，六（1）班的小明选了“喜欢乒乓球”，那么小明被选中的可能性大小是____________．

【答案】（1）六（1）班喜欢乒乓球的人数为16人；（2）20，36；（3）

【详解】试题分析：（1）根据喜欢篮球的有12人，占30%，即可求得总人数，利用总人数乘40%，即可求得喜欢乒乓球的人数；

（2）利用百分比的计算公式，即可求得m的值，利用360°乘以对应的百分比，即可求得圆心角的度数；

（3）参加学校的乒乓队的概率就是用参加学校的乒乓队的人数除以班级喜欢乒乓球的人数即可．

试题解析：（1）（人）

答：六（1）班喜欢乒乓球的人数为16人．

（2）=40（人），840=，

360°×（1-30-40）=360°×=36°，

故答案为20，36；

（3）小明被选中的可能性大小是=.

点睛：此题考查的是扇形统计图.读懂统计图，从统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.

12．（2022·黑龙江·绥棱县克音河乡学校阶段练习）新华书店今年5月份销售图书4000本，下图表示的是各种图书的销售情况．

(1)从图上可知，销售最多的是（    ）书；销售最少的是（    ）书．

(2)侦探书销售了1000本，占5月份图书销售量的（    ）%．

(3)文艺书的销售量占5月份图书销售量的23%，5月份销售卡通书多少本？

【答案】(1)科普，卡通

(2)25

(3)280本

【分析】（1）根据图中各种书所占的百分比即可得；

（2）利用侦探书的销售量除以今年5月份销售图书的总量即可得；

（3）先求出卡通书的占比，再乘以今年5月份销售图书的总量即可得．

（1）

解：由图可知，侦探书和卡通书占比为，且侦探书的占比大于卡通书的占比，

所以销售最多的是科普书；销售最少的是卡通书，

故答案为：科普，卡通．

（2）

解：，

则侦探书销售了1000本，占5月份图书销售量的，

故答案为：25．

（3）

解：（本），

答：5月份销售卡通书280本．

【点睛】本题考查了扇形统计图，百分数的应用，读懂统计图中数据所含的意义是解题关键．

13．（2022·黑龙江·哈尔滨市第六十九中学校开学考试）一块400平方米的菜地，四种蔬菜的种植面积分布如图所示．

(1)西红柿和辣椒的种植面积分别是多少平方米？

(2)如果豆角每平方米的产量是12千克，因不能及时采摘导致损耗，实际共采摘豆角1368千克，求损耗了多少千克？

【答案】(1)西红柿和辣椒的种植面积分别为100、60平方米．

(2)损耗了72千克

【分析】（1）根据分数乘法的意义，用菜地的面积乘上西红柿和辣椒的种植面积所占的百分比，就是它们的种植面积；

（2）先计算出豆角的种植面积占的百分率，即1-30%-25%-15%=30%，再用总面积乘上豆角的种植面积占的百分率，即可求出豆角的种植面积；然后乘上每平方米豆角的产量，就是总产量；进而用总产量减去实际的产量，就是损耗的产量，用损耗的产量除以总产量，再乘上百分之百，就是损耗率．

（1）

400×25%=100（平方米），

400×15%=60（平方米），

答：西红柿和辣椒的种植面积分别为100、60平方米．

（2）

豆角种植面积为400×（1-30%-25%-15%），

=400×30%，

=120（平方米）；

豆角实际产量：120×12=1440（千克），

损耗量为1440-1368=72，

答：损耗了72千克．

【点睛】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息，然后再根据基本的数量关系解决问题．

14．（2021·上海市彭浦初级中学期末）在抗震救灾的捐款活动中，六（2）班同学的捐款人数情况如图所示，其中捐款10元的人数为10人，请根据图像回答下列问题：

(1)捐款50元的人所在扇形的圆心角是____________度．

(2)六（2）班共有____________名学生．

(3)捐款100元的人数是____________人．

(4)捐款5元的人数是____________人．

(5)捐款20元的人数是____________人．

【答案】(1)54

(2)40

(3)5

(4)4

(5)15

【分析】（1）用捐款50元的人所占百分比乘以360°即可得答案；

（2）根据捐款10元的人所在扇形的圆心角度数可得其所占百分比，用10除以捐款10元的人所占百分比即可得答案；

（3）用总人数乘以捐款100元的人所占份数即可得答案；

（4）根据捐款20元的人所在扇形的圆心角的度数，可得其所占百分比，即可求出捐款5元的人所占百分比，乘以总人数即可得答案；

（5）用捐款20元的人所占百分比，乘以总人数即可得答案．

（1）

∵捐款50元的人所占百分比为15%，

∴捐款50元的人所在扇形的圆心角是360°×15%=54°，

故答案为：54

（2）

∵捐款10元的人所在扇形的圆心角为90°，

∴捐款10元的人所占百分比为90÷360×100%=25%，

∵捐款10元的人数为10人，

∴六（2）班共有学生10÷25%=40（人），

故答案为：40

（3）

∵捐款100元的人所占份数为，

∴捐款100元的人数为40×=5（人）

故答案为：5

（4）

∵捐款20元的人所在扇形的圆心角的度数为135°，

∴捐款20元的人所占百分比为135°÷360°=，

∴捐款5元的人所占百分比为1-15%-25%--=10%，

∴捐款5元的人数是40×10%=4（人），

故答案为：4

（5）

∵捐款20元的人所占百分比为，

∴捐款20元的人数为40×=15（人），

故答案为：15．

【点睛】本题考查扇形统计图及百分数的应用，正确提取统计图中信息是解题关键．