

2020-2021学年江苏省上冈高级中学等四校联考高一(下)期中数学试卷
展开2020-2021学年江苏省上冈高级中学等四校联考高一(下)期中数学试卷
一、单选题(共40分)
1.(5分)若为虚数单位,,,且,则复数的模等于
A. B. C. D.
2.(5分)若点为角终边上一点,则的值为
A. B. C. D.
3.(5分)已知向量,,且与共线,那么的值为
A.1 B.2 C.3 D.4
4.(5分)在正方体中为底面的中心,为的中点,则异面直线与所成角的正弦值为
A. B. C. D.
5.(5分)已知复数满足为虚数单位),且,则正数的值为
A.2 B.1 C. D.
6.(5分)已知的面积为,,,则
A. B. C. D.
7.(5分)设非零向量,夹角为,若,且不等式对任意恒成立,则实数的取值范围为
A., B., C., D.,
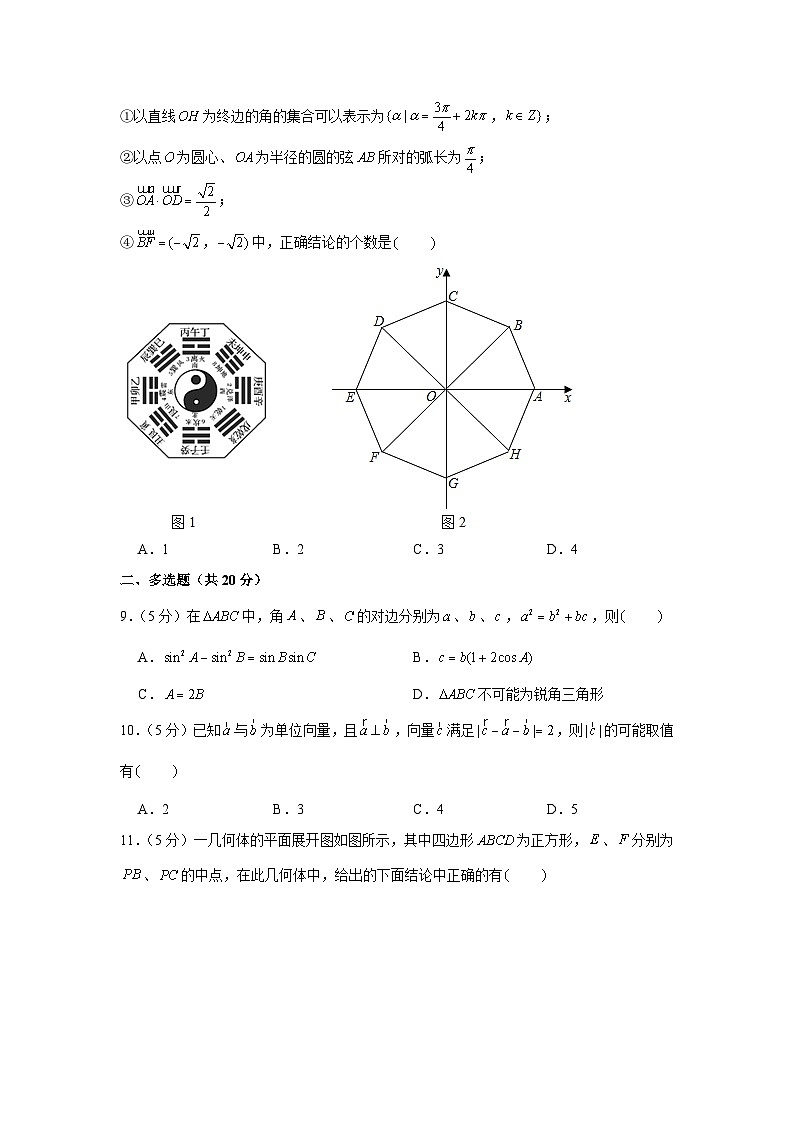
8.(5分)古代中国的太极八卦图是以同圆内的圆心为界,画出相等的两个阴阳鱼,阳鱼的头部有个阴眼,阴鱼的头部有个阳眼,表示万物都在相互转化,互相渗透,阴中有阳,阳中有阴,阴阳相合,相生相克,蕴含现代哲学中的矛盾对立统一规律.图2(正八边形是由图1(八卦模型图)抽象而得到,并建立如图2平面直角坐标系,设.则下述四个结论:
①以直线为终边的角的集合可以表示为,;
②以点为圆心、为半径的圆的弦所对的弧长为;
③;
④,中,正确结论的个数是
A.1 B.2 C.3 D.4
二、多选题(共20分)
9.(5分)在中,角、、的对边分别为、、,,则
A. B.
C. D.不可能为锐角三角形
10.(5分)已知与为单位向量,且,向量满足,则的可能取值有
A.2 B.3 C.4 D.5
11.(5分)一几何体的平面展开图如图所示,其中四边形为正方形,、分别为、的中点,在此几何体中,给出的下面结论中正确的有
A.直线与直线异面 B.直线与直线异面
C.直线平面 D.直线平面
12.(5分)已知函数,有下列四个结论,其中正确的结论为
A.在区间上单调递增
B.是的一个周期
C.的值域为
D.的图象关于轴对称
三、填空题(共20分)
13.(5分)计算: .
14.(5分)已知中,角,,的对边分别为,,,若,则 .
15.(5分)在中,,,,为线段上一点,则的最小值为 .
16.(5分)在中,若,,则的最小值为 ,面积的最大值为 .
四、解答题(共70分)
17.(10分)已知函数
(1)若,求的值;
(2)设三内角,,所对边分别为,,,且,求在,上的值域.
18.(12分)已知复数同时满足下列两个条件:
①的实部和虚部都是整数,且在复平面内对应的点位于第四象限.
②
(Ⅰ)求出复数;
(Ⅱ)求
19.(12分)如图,四棱锥,平面,四边形是直角梯形,,,,为中点.
(1)求证:平面;
(2)求证:.
20.(12分)在平面直角坐标系中,已知四边形是等腰梯形,,点,满足,点在线段上运动(包括端点),如图.
(1)求的余弦值;
(2)是否存在实数,使,若存在,求出满足条件的实数的取值范围,若不存在,请说明理由.
21.(12分)如图,直角中,点,在斜边上,异于,,且在,之间).
(1)若是角的平分线,,且,求三角形的面积;
(2)已知,,,设.
①若,求的长;
②求面积的最小值.
22.(12分)已知向量.
求函数的单调增区间.
(2)若方程上有解,求实数的取值范围.
(3)设,已知区间,,且满足:在,上至少含有100个零点,在所有满足上述条件的,中求的最小值.
2020-2021学年江苏省上冈高级中学等四校联考高一(下)期中数学试卷
参考答案与试题解析
一、单选题(共40分)
1.【分析】把已知等式变形,利用复数代数形式的乘法运算化简,再由复数相等的条件求得,的值,则答案可求.
【解答】解:由,得
,
,,
则的模等于.
故选:.
2.【分析】直接利用三角函数的定义,三角函数的值,倍角公式的应用求出结果.
【解答】解:点为角终边上一点,
利用三角函数的定义解得:;;
所以,;
故.
故选:.
3.【分析】利用向量的运算法则求出两个向量的和;利用向量共线的充要条件列出方程求出;利用向量的数量积公式求出值.
【解答】解:
共线
解得
故选:.
4.【分析】先作出异面直线与所成角,再在中即可得解.
【解答】解:取中点,连接,
则,
则为异面直线与所成角,
设,
在中,
,,
即,
故选:.
5.【分析】把已知等式变形,再由复数代数形式的乘除运算化简求得,结合复数模的计算公式求解.
【解答】解:由,得,则,
由,得,即.
故选:.
6.【分析】由已知利用三角形面积公式可求的值,进而利用余弦定理即可计算得解的值.
【解答】解:,,的面积为,
解得:,
.
故选:.
7.【分析】由题意先利用平面向量数量积的运算法则进行转化,然后结合函数的恒成立问题即可求解.
【解答】解:非零向量,夹角为,若,
,
不等式对任意恒成立
,
,
整理可得,恒成立,
,,
,
,
故选:.
8.【分析】①根据任意角的概念即可判断;②利用弧长公式即可判断;③利用向量数量积即可判断;④利用向量的坐标运算公式即可判断.
【解答】解:①由题意可知,以直线为终边的角的集合表示为,故①错误;
②弧长,其中,以点为圆心、为半径的圆的弦 所对的弧长,故②正确;
③,故③错误;
④,,故④正确.
综上所述,正确的结论个数为2,
故选:.
二、多选题(共20分)
9.【分析】对于项,在中,由正弦定理即可求解判断.
对于项,假设,利用余弦定理即可求解.
对于项,由结论,利用正弦定理,两角和与差的正弦公式化简可得,进而可求,即可判断得解.
对于项,在中,由余弦定理可得,设,,,可得角最大,且,即为锐角,可得可能为锐角三角形,即可判断得解.
【解答】解:在中,角、、的对边分别为、、,,
对于项,在中,由正弦定理可得,
即,故项正确;
对于项,在中,由余弦定理可得,
假设,
等式右边等式左边,
则假设成立,故项正确;
对于项,因为,利用正弦定理可得,
又,
所以可得,
可得,或,
所以,或(舍去),
故项正确;
对于项,在中,由余弦定理可得,
设,,,满足,
此时角最大,且,即为锐角,
故可能为锐角三角形,故项错误.
故选:.
10.【分析】根据题意,设,,,以为坐标原点,的方向为轴正方向,的方向为轴的正方向建立坐标系,分析、的坐标,设,由向量的坐标计算公式可得,进而由向量模的计算公式可得,分析可得点的轨迹,结合点与圆的位置关系分析可得答案.
【解答】解:根据题意,设,,,
以为坐标原点,的方向为轴正方向,的方向为轴的正方向建立坐标系,
则,,设,
则,
若,则有,则在以为圆心,半径为2的圆上,
设为点,则,则有,
即,
则的取值范围为,;
分析选项:符合;
故选:.
11.【分析】把展开图恢复成四棱锥,作出图形,易知正确;由线面平行的判定定理可证正确;由为等腰梯形可否定,.
【解答】解:如图,把几何体恢复原状,显然,异面,可知正确;
,,
,
平面,可知正确;
易知为等腰梯形,可知,错误.
故选:.
12.【分析】直接利用三角函数的关系式的变换,二次函数的性质,函数的单调性,函数的值域的应用判断、、、的结论.
【解答】解:函数,
对于:由于函数:,,,,故错误;
对于:由于函数不为周期函数,故错误;
对于:当时,,所以;
当时,,所以;
当时,,所以;
当时,,所以;
当时,,所以;故的值域为,故正确.
对于:根据函数,故函数为偶函数,故函数的图象关于轴对称,故正确;
故选:.
三、填空题(共20分)
13.【分析】利用复数代数形式的加减运算与复数模的求法计算得答案.
【解答】解:
.
故答案为:.
14.【分析】方法一:依题意可得,进而由余弦定理可化得,根据三角函数恒等变换的应用及余弦定理化简所求即可求值得解;
方法二:由已知可求,根据三角函数恒等变换的应用化简所求即可求值得解;
【解答】解:方法一:依题意,,
故,
即,可化得,
故
.
方法二:依题意,,
故,
即,
故.
故答案为:.
15.【分析】以为坐标原点,,所在直线为,轴建立直角坐标系,求得,,的坐标,即有直线的方程,设,求得,的坐标,再由向量的平方即为模的平方,转化为二次函数的最值,即可求得的最小值.
【解答】解:以为坐标原点,,所在直线为,轴建立直角坐标系,
可得,,,,
则直线的方程为,
设,则,,
,,,
则
,
由,,
可得的最小值为.
故答案为:.
16.【分析】根据余弦定理可得,将化为可得,面积化为可得.
【解答】解:因为,,,
由余弦定理得,,
(当且仅当时取等)
,
的面积为.
故答案为:,.
四、解答题(共70分)
17.【分析】(1)把代入整理可得,,利用二倍角公式化简可求
(2)由,利用余弦定理可得,,即,再由正弦定理化简可求,对函数化简可得,由可求.
【解答】解:(1)由,得.
.
,
即,
.(5分)
(2)由,即,
得,
则,
又为三角形内角,
,(8分)
又(10分)
由,则,
故,
即值域是,.(12分)
18.【分析】(Ⅰ)利用已知条件,设出复数,通过求出即可复数;
(Ⅱ)化简为的形式,然后利用复数的模求解即可.
【解答】解:由题意设复数,,,,.
(Ⅰ),可得:,
可得,
可得,解得
,,,,.
可得,,
.
(Ⅱ).
19.【分析】(1)取的中点,证出,再利用线面平行的判定定理即可证出.
(2)利用线面垂直的判定定理可证出平面,再根据线面垂直的定义即可证出.
【解答】证明:(1)如图,取的中点,连接,,
为中点,,且,
又,,,,
为平行四边形,即,
又平面,平面,
所以平面.
(2)平面,平面,,
又,,,
,平面,平面,
平面,
又平面,.
20.【分析】(1)由题意求得、的坐标,再根据,,运算求得结果.
(2)设,其中,由,得,可得.再根据,,,求得实数的取值范围.
【解答】解:(1)由题意可得,,
故,.
(2)设,其中,,.
若,
则,
即,
可得.
若,则不存在,
若,则,
,,,
故.
21.【分析】(1)由角分线定理得,再分别在和中,利用余弦定理列出关于和的方程组,解之即可得解;
(2)①且为锐角,,然后在和中,利用正弦定理可分别求得,,;
②在和中,由正弦定理分别求得和(均用含的式子表示),所以,
然后令,求得其在上的最大值,即可得到面积的最小值
【解答】解:(1)是角的平分线,,
由角分线定理可知,即,
设,,,
由余弦定理得:
在中,,整理得,①
在中,,整理得,②
由①②解得,,
.
(2),,,,
①且为锐角,,
在中,,
由正弦定理得:,代入数据求得,,,
在中,,,
由正弦定理得:,解得.
②由正弦定理可知,
在中,,
在中,,
,
令,,
,
当即时,,
此时面积取得最小值,为.
22.【分析】(1)由向量的数量积的坐标表示和三角函数的恒等变换公式,化简,再由正弦函数的增区间,解不等式可得所求;
(2)令,由正弦函数的图象可得的范围,由参数分离和二次函数的值域,可得所求的范围;
(3)解,可得的零点相离间隔依次为和,由题意可得若最小,则和都是零点,此时在区间,,,,,,分别恰有3,5,,个零点,即可得到所求最小值.
【解答】解:(1)向量.
即有,
由,解得,
则的增区间为,,;
(2)令,由,可得,,,,
方程上有解,
即为在,有解,
即为,由,可得,,
可得的范围是,;
(3),
由,可得或,,
即为或,,
即的零点相离间隔依次为和,
在,上至少含有100个零点,
若最小,则和都是零点,
此时在区间,,,,,,
分别恰有3,5,,个零点,
所以在区间,是恰有99个零点,从而在区间,至少有一个零点,
,即,
则的最小值为.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2022/3/11 19:16:15;用户:高中数学6;邮箱:tdjyzx38@xyh.com;学号:42412367
2020-2021学年江苏省无锡市江阴市四校联考高二(上)期中数学试卷: 这是一份2020-2021学年江苏省无锡市江阴市四校联考高二(上)期中数学试卷,共19页。试卷主要包含了命题“,”的否定是 ,是直线和直线平行的 条件,直线的倾斜角的取值范围是 等内容,欢迎下载使用。
2020-2021学年江苏省南京市六校联考高一(下)期中数学试卷: 这是一份2020-2021学年江苏省南京市六校联考高一(下)期中数学试卷,共16页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年江苏省江阴二中、要塞中学等四校高一(上)期中数学试卷: 这是一份2020-2021学年江苏省江阴二中、要塞中学等四校高一(上)期中数学试卷,共19页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。












