2024版高考数学一轮复习教材基础练第三章导数及其应用第三节导数与函数的极值最值教学课件

这是一份2024版高考数学一轮复习教材基础练第三章导数及其应用第三节导数与函数的极值最值教学课件，共42页。PPT课件主要包含了教材知识萃取，函数的极值，极小值点，极值点，易错警示，4得出结论，方法技巧，教材素材变式，辨析比较等内容，欢迎下载使用。

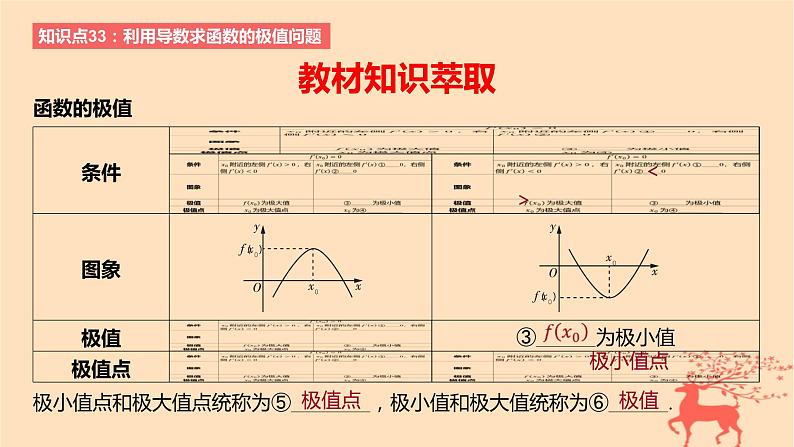
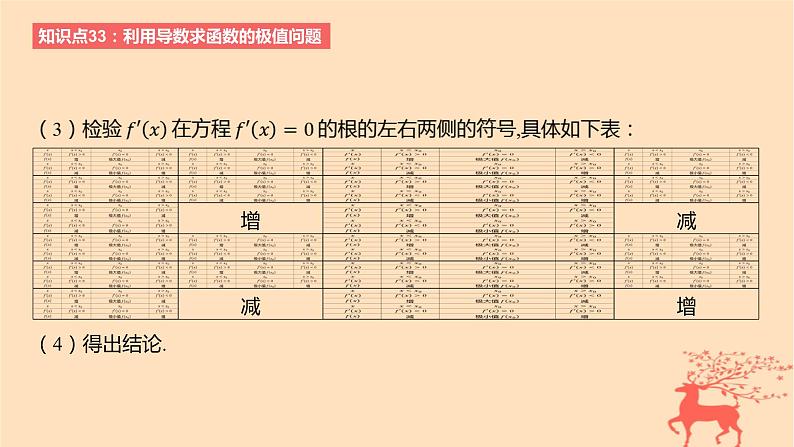
知识点33：利用导数求函数的极值问题
极小值点和极大值点统称为⑤________，极小值和极大值统称为⑥______.
方法技巧根据函数图象判断极值的方法
（1）先找导数为0的点，再判断导数为0的点的左、右两侧的导数符号，进而判断函数极值的情况.
1.已知函数极值点或极值求参数的两个要领
2. 函数f(x)的定义域为R,其导函数f '(x)的图象如图所示,则函数f(x)极值点的个数为A.2B.3C.4D.5
5. 设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则A.abC.aba2
优解(特值排除法)　当a=1,b=2时,函数f(x)=(x-1)2·(x-2),画出该函数的图象如图1所示,可知x=1为函数f(x)的极大值点,满足题意.从而,根据a=1,b=2可判断选项B,C错误.当a=-1,b=-2时,函数f(x)=-(x+1)2(x+2),画出该函数的图象如图2所示,可知x=-1为函数f(x)的极大值点,满足题意.从而,根据a=-1,b=-2可判断选项A错误.综上,选D.
光速解(数形结合法)　当a>0时,根据题意画出函数f(x)的大致图象,如图3所示,观察可知b>a.当a<0时,根据题意画出函数f(x)的大致图象,如图4所示,观察可知a>b.(难点突破:熟练掌握三次函数的图象特征,有利于根据题意迅速画图分析)综上,可知必有ab>a2成立.故选D.
6. 若函数f(x)=x3-3ax+1在区间(0,1)上有极小值,则a的取值范围为　　　　. 
知识点34：利用导数求函数的最值问题
函数极值与最值的区别与联系
方法技巧“和差型”函数的构造技巧
方法技巧“商型”函数的构造技巧
方法技巧“积型”函数的构造技巧
方法技巧对称构造法求解极值点偏移问题的步骤
方法技巧导数中的重要不等式链
函数与导数大题的做题规范
【变式探究】若函数f(x)=x3+x2-5x-2在区间(m,m+5)内有最小值,则实数m的取值范围是A.(-4,1)B.(-4,0)C.[-3,1)D.(-3,1)