备战2024高考一轮复习数学（理） 第三章 导数及其应用 第三节 导数与函数的极值、最值课件PPT

这是一份备战2024高考一轮复习数学（理） 第三章 导数及其应用 第三节 导数与函数的极值、最值课件PPT，共38页。PPT课件主要包含了函数的极值与导数，答案C等内容，欢迎下载使用。

2．函数的最值与导数(1)在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．(2)若函数f(x)在[a，b]上单调递增，则 为函数的最小值， 为函数的最大值；若函数f(x)在[a，b]上单调递减，则 为函数的最大值， 为函数的最小值．
3．函数极值与最值的区别与联系
(1)极值点不是点，若函数f(x)在x1处取得极大值，则x1为极大值点，极大值为f(x1)．(2)极大值与极小值没有必然关系，极小值可能比极大值还大．(3)有极值的函数一定不是单调函数．(4)f′(x0)＝0是x0为可导函数f(x)的极值点的必要不充分条件．例如，f(x)＝x3，f′(0)＝0，但x＝0不是极值点．
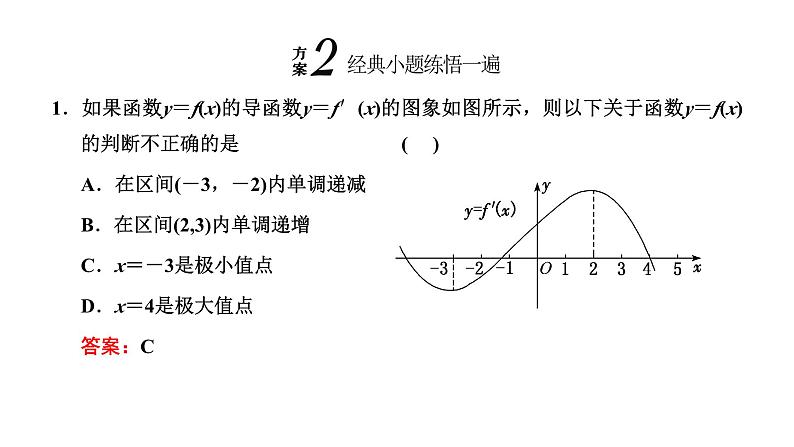
1．如果函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则以下关于函数y＝f(x)的判断不正确的是(　 )A．在区间(－3，－2)内单调递减B．在区间(2,3)内单调递增C．x＝－3是极小值点D．x＝4是极大值点答案：C
4．已知函数f(x)＝x3－12x＋8在区间[－3,3]上的最大值与最小值分别为M，m，则M－m＝________.解析：令f′(x)＝3x2－12＝0，解得x＝±2.计算f(－3)＝17，f(－2)＝24，f(2)＝－8，f(3)＝－1，所以M＝24，m＝－8，故M－m＝32.答案：325．设x1，x2是函数f(x)＝x3－2ax2＋a2x的两个极值点，若x1＜2＜x2，则实数a的取值范围是________．解析：由题意得f′(x)＝3x2－4ax＋a2的两个零点x1，x2满足x1＜2＜x2，所以f′(2)＝12－8a＋a2＜0，解得2＜a＜6.答案：(2,6)
层级一/ 基础点——自练通关(省时间)基础点(一)　已知图象判断函数的极值、最值　[题点全训]1．如图是函数y＝f(x)的导函数的图象，下列结论中不正确的是(　 )A．f(x)在[－2，－1]上是减函数B．当x＝3时，f(x)取得最小值C．当x＝－1时，f(x)取得极小值D．当x＝2时，f(x)取得极大值解析：根据图象知当x∈(－2，－1)，x∈(2,4)时，f′(x)<0，函数f(x)单调递减；当x∈(－1,2)，x∈(4，＋∞)时，f′(x)>0，函数f(x)单调递增，故A、C、D正确；当x＝3时，f(x)不是取得最小值，B错误．答案：B　
2.设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(x－1)3·f′(x)的图象如图所示，则下列结论中正确的是(　 )A．函数f(x)有极大值f(－3)和f(3)B．函数f(x)有极小值f(－3)和f(3)C．函数f(x)有极小值f(3)和极大值f(－3)D．函数f(x)有极小值f(－3)和极大值f(3)解析：结合题目所给图象进行分段分析，当x<－3时，(x－1)3<0，得f′(x)<0；当－30；当10，得f′(x)>0；当x>3时，(x－1)3>0，得f′(x)<0.根据极值点的定义可知，当x＝－3时，f(x)取得极小值f(－3)，当x＝3时，f(x)取得极大值f(3)，x＝1的左右两边导函数值都大于零，因此不是原函数的极值点．答案：D　
[一“点”就过]导函数图象的应用策略(1)由y＝f′(x)的图象与x轴的交点，可得函数y＝f(x)的可能极值点；(2)由导函数y＝f′(x)的图象可以看出y＝f′(x)的值的正负，从而可得函数y＝f(x)的单调性，进而研究函数的极值、最值．
4．已知f(x)＝2x3－6x2＋m(m为常数)在[－2,2]上有最大值3，那么此函数在[－2,2]上的最小值是________．解析：∵f′(x)＝6x2－12x＝6x(x－2)，∴f(x)在(－2，0)上为增函数，在(0,2)上为减函数，∴当x＝0时，f(0)＝m最大，∴m＝3.∵f(－2)＝－37，f(2)＝－5，∴最小值为－37.答案：－37
[一“点”就过]1．函数极值和极值点的求解步骤(1)确定函数的定义域；(2)求方程f′(x)＝0的根；(3)用方程f′(x)＝0的根顺次将函数的定义域分成若干个小开区间，并列成表格；(4)由f′(x)在方程f′(x)＝0的根左右的符号，来判断f(x)在这个根处取极值的情况．
2．求函数f(x)在[a，b]上的最值的方法(1)若函数f(x)在区间[a，b]上单调递增(或递减)，则f(a)为最小(大)值，f(b)为最大(小)值．(2)若函数在区间[a，b]内有极值，则要先求出函数在(a，b)内的极值，再与f(a)，f(b)比较，最大的是最大值，最小的是最小值，可列表完成．(3)函数f(x)在区间(a，b)上有唯一一个极值点，这个极值点就是最大(或最小)值点，此结论在导数的实际应用中经常用到．
求解函数极值点问题的注意点(1)导数为零的点不一定是极值点．在求得导函数的零点后，要利用导函数零点左右的导函数符号来确定极值点．(2)对于求解析式中含有参数的函数极值问题，一般要对方程f′(x)＝0的根的情况进行讨论，分两个层次讨论．第一层次，讨论在定义域内是否有根；第二层次，在有根的条件下，再讨论根的大小．(3)对于涉及极值点的不等式证明问题，一般要进一步构造函数并借助导数研究函数的单调性，进而借助不等式去解决．　　
根据函数极值情况求参数的两个要领(1)列式：根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解．(2)验证：求解后验证根的合理性．　　
[解]　(1)因为f(x)＝excs x－x，所以f′(x)＝ex(cs x－sin x)－1，f′(0)＝0.又因为f(0)＝1，所以曲线y＝f(x)在点(0，f(0))处的切线方程为y＝1.
导数法求给定区间上函数的最值问题的一般步骤(1)求函数f(x)的导数f′(x)；(2)求f(x)在给定区间上的单调性和极值；(3)求f(x)在给定区间上的端点值；(4)将f(x)的各极值与f(x)的端点值进行比较，确定f(x)的最大值与最小值；(5)反思回顾，查看关键点，易错点和解题规范．　　
[针对训练]1．已知函数f(x)＝ex＋x2＋(a－2)x＋1在区间(0,1)上有最小值，则实数a的取值范围是(　 )A．(－e,1) B．(1－e,1)C．(－e，＋∞) D．(0，e)
2．已知a是实数，函数f(x)＝x2(x－a)．(1)若曲线y＝f(x)在x＝1处的切线l与直线3x－y＝0平行，求切线l的方程；(2)求f(x)在区间[0,2]上的最小值．解：(1)f′(x)＝3x2－2ax.因为f′(1)＝3－2a＝3，所以a＝0，又当a＝0时，f(1)＝1，f′(1)＝3，则切点坐标为(1,1)，斜率为3，所以曲线y＝f(x)在点(1，f(1))处的切线方程为y－1＝3(x－1)，化简得3x－y－2＝0.
层级三/ 细微点——优化完善(扫盲点)1.(混淆极值与最值)已知定义在R上的函数f(x)，其导函数f′(x)的大致图象如图所示，则下列叙述正确的是(　 )A．f(b)>f(a)>f(c)B．函数f(x)在x＝c处取得极小值，在x＝e处取得极大值C．函数f(x)在x＝c处取得极大值，在x＝e处取得极小值D．函数f(x)的最小值为f(d)解析：由题图可知，当x≤c时，f′(x)≥0，所以函数f(x)在(－∞，c]上单调递增，又a0；当ce时，f′(x)>0.所以函数f(x)在x＝c处取得极大值，在x＝e处取得极小值，故B不正确，C正确．由题图可知，当d≤x≤e时，f′(x)≤0，所以函数f(x)在[d，e]上单调递减，从而f(d)>f(e)，所以D不正确．故选C.
2．(由函数的极值求参数忽略验证)已知函数f(x)＝x3＋3mx2＋nx＋m2在x＝－1处取得极值0，则m＋n＝(　 )A．4 B．11 C．4或11 D．3或9
3．(渗透“五育”教育)某中学开展劳动实习，学习加工制作模具，有一个模具的毛坯直观图如图所示，是由一个圆柱与两个半球对接而成的组合体，其中圆柱的底面半径为1，高为2，半球的半径为1.现要在该毛坯的内部挖出一个中空的圆柱形空间，该中空的圆柱形空间的上下底面与毛坯的圆柱体底面平行，挖出中空的圆柱形空间后模具制作完成，则该模具体积的最小值为________．
解析：作出该模具的轴截面，如图所示，其中AB为圆柱底面直径，O为上底面圆心，CD为圆柱下底面直径，四边形EFGH为挖去的圆柱形的轴截面，连接OF，记∠FOB＝θ.挖去的圆柱形体积V＝π(cs θ)2(2sin θ＋2)＝2π(1－sin2θ)(1＋sin θ)．
4．(强化开放思维)能说明“若f′(0)＝0，则x＝0是函数y＝f(x)的极值点”为假命题的一个函数是________________．解析：极值点的导数必须为零，且极值点左右两侧的函数单调性相反．函数f(x)＝x3，当x＝0时，f′(0)＝0，但是f(x)＝x3在R上单调递增，所以x＝0不是函数f(x)＝x3的极值点．答案：f(x)＝x3或f(x)＝1等(答案不唯一)
“课时验收评价”见“课时验收评价(十六)” (单击进入电子文档)