2023年云南省昭通市昭阳区中考数学一模试卷（含解析）

2023年云南省昭通市昭阳区中考数学一模试卷

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1.  昭通是历史上中原文化进入云南的重要通道，是中国“南丝绸之路”的要冲，气候宜人今年月某日的最高气温为，最低气温为，则该日的最大温差为(    )

A.  B.  C.  D.

2.  如图，已知，，则的度数是(    )

A.
B.
C.
D.

3.  如图是由个完全相同的小正方体摆成的几何体，则这个几何体俯视图是(    )

A.
B.
C.
D.

4.  年冬奥运即将在北京举行，北京也即将成为迄今为止唯一个既举办过夏季奥运会，又举办过冬季奥运会的城市，据了解北京冬奥会的预算规模为亿美元，政府补贴万美元其中用科学记数法表示为(    )

A.  B.  C.  D.

5.  下列计算正确的是(    )

A.  B.
C.  D.

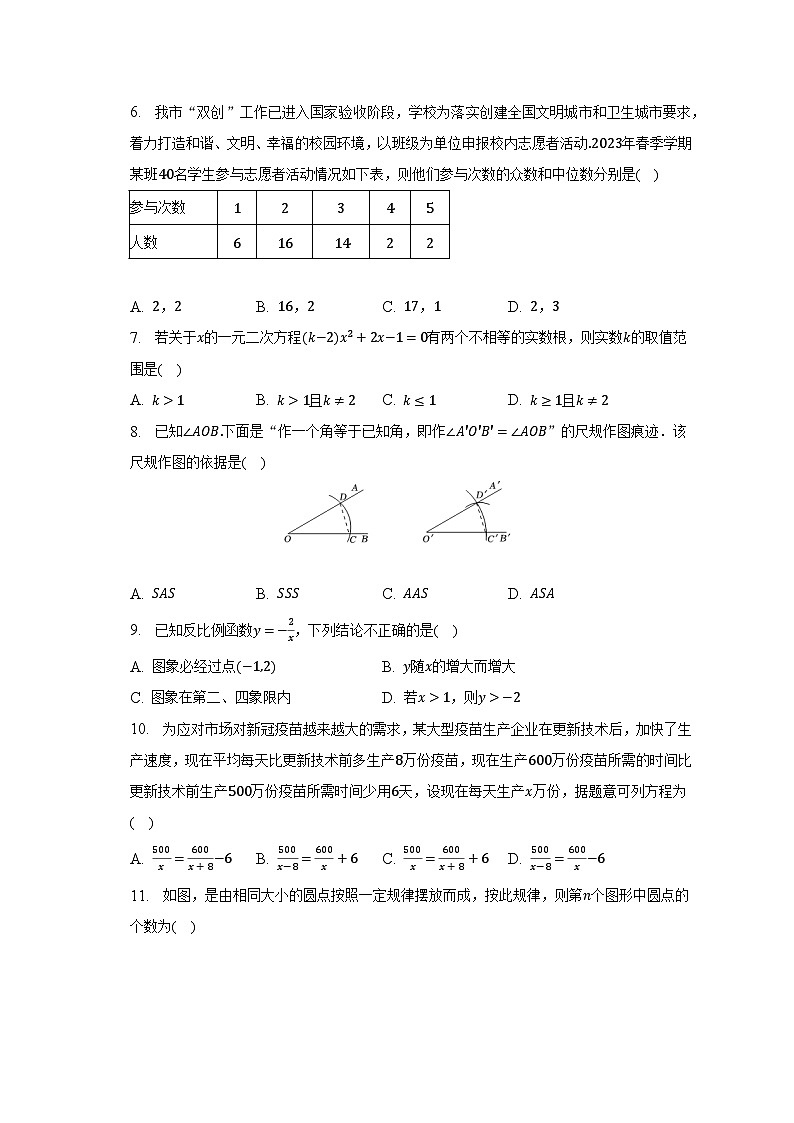
6.  我市“双创”工作已进入国家验收阶段，学校为落实创建全国文明城市和卫生城市要求，着力打造和谐、文明、幸福的校园环境，以班级为单位申报校内志愿者活动年春季学期某班名学生参与志愿者活动情况如下表，则他们参与次数的众数和中位数分别是(    )

A. ， B. ， C. ， D. ，

7.  若关于的一元二次方程有两个不相等的实数根，则实数的取值范围是(    )

A.  B. 且 C.  D. 且

8.  已知下面是“作一个角等于已知角，即作”的尺规作图痕迹．该尺规作图的依据是(    )

A.  B.  C.  D.

9.  已知反比例函数，下列结论不正确的是(    )

A. 图象必经过点 B. 随的增大而增大
C. 图象在第二、四象限内 D. 若，则

10.  为应对市场对新冠疫苗越来越大的需求，某大型疫苗生产企业在更新技术后，加快了生产速度，现在平均每天比更新技术前多生产万份疫苗，现在生产万份疫苗所需的时间比更新技术前生产万份疫苗所需时间少用天，设现在每天生产万份，据题意可列方程为(    )

A.  B.  C.  D.

11.  如图，是由相同大小的圆点按照一定规律摆放而成，按此规律，则第个图形中圆点的个数为(    )

 

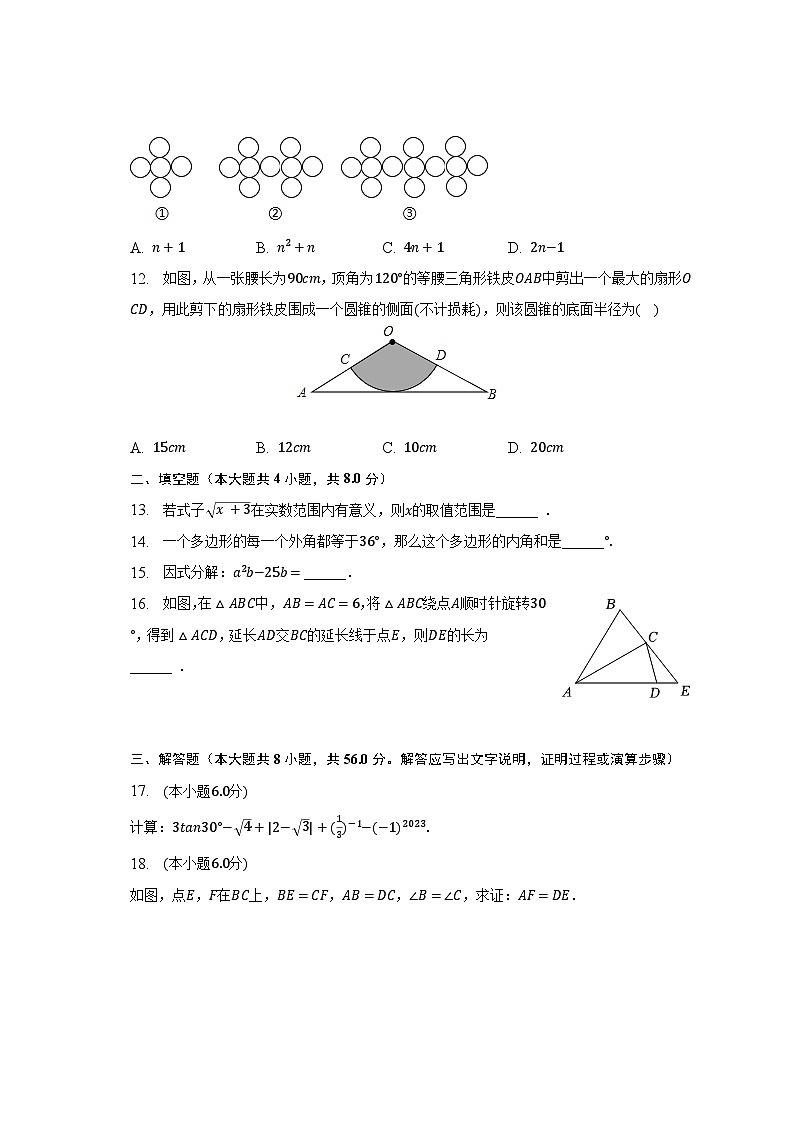
A.  B.  C.  D.

12.  如图，从一张腰长为，顶角为的等腰三角形铁皮中剪出一个最大的扇形，用此剪下的扇形铁皮围成一个圆锥的侧面不计损耗，则该圆锥的底面半径为(    )

A.  B.  C.  D.

二、填空题（本大题共4小题，共8.0分）

13.  若式子在实数范围内有意义，则的取值范围是______ ．

14.  一个多边形的每一个外角都等于，那么这个多边形的内角和是______

15.  因式分解：______．

16.  如图，在中，，将绕点顺时针旋转，得到，延长交的延长线于点，则的长为______ ．

三、解答题（本大题共8小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）

17.  本小题分
计算：．

18.  本小题分
如图，点，在上，，，，求证：．

 

19.  本小题分
为了了解昭阳区“新冠肺炎”疫情防控期间九年级学生线上学习情况，通过问卷就“你对自己线上学习的效果评价”进行了调查，从中随机抽取了部分样卷进行统计，绘制了如图的统计图．

根据统计图信息，解答下列问题：
本次调查的样本容量为______ ；并补全条形统计图；
扇形统计图中“较好”对应的扇形圆心角的度数为______ ；
若全区九年级线上学习人数有人，请估计对线上学习评价“非常好”的人数．

20.  本小题分
对垃圾进行分类投放，能提高垃圾处理和再利用的效率，减少污染，保护环境为了检查垃圾分类的落实情况，某居委会成立了甲、乙两个检查组，采取随机抽查的方式分别对辖区内的，，，四个小区进行检查，并且每个小区不重复检查．
甲组抽到小区的概率是______ ；
请用列表或画树状图的方法求甲组抽到小区，同时乙组抽到小区的概率．

21.  本小题分
如图，平行四边形中，，过点作交的延长线于点，点为的中点，连接．
求证：四边形是矩形；
若，且，求四边形的面积．

22.  本小题分
某果园苹果丰收，首批采摘吨，计划租用，两种型号的汽车共辆，一次性运往外地销售．、两种型号的汽车的满载量和租车费用如下：

设租型汽车辆，总租车费用为元．
求与之间的函数关系式；
总租车费用最少是多少元？并说明此时的租车方案．

23.  本小题分
如图，抛物线与轴交于点和点点在原点的左侧，点在原点的右侧，与轴交于点，．
求该抛物线的函数解析式；
连接，点是直线上方抛物线上的点，连接，，交于点，当：最大时，求点的坐标．

24.  本小题分
如图，在中，，动点从点开始沿以的速度向点移动，动点从点开始沿以的速度向点移动如果、分别从、同时移动，移动时间为．
以为直径的与交于点，当为何值时，与相切；
是否存在为等腰三角形？若存在，求出相应的值；若不存在请说明理由．

答案和解析

1.【答案】 

【解析】解：根据题意得：，
则该日的最大温差为．
故选：．
根据题意列出算式，计算即可得到结果．
此题考查了有理数的减法，以及正数和负数，熟练掌握运算法则是解本题的关键．
 

2.【答案】 

【解析】解：如图，

，，
，
故选：．
先根据平行线的性质，得到的度数，再根据邻补角进行计算即可．
本题主要考查了平行线的性质，应用的知识点为：两直线平行，内错角相等；邻补角互补．
 

3.【答案】 

【解析】解：俯视图如选项B所示，
故选：．
根据从上面看得到的图象是俯视图，可得答案．
本题考查了简单组合体的三视图，从上面看的到的视图是俯视图．
 

4.【答案】 

【解析】解：   用科学记数法表示为．
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正数；
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 

5.【答案】 

【解析】解：、原式，故本选项计算错误．
B、原式，故本选项计算错误．
C、原式，故本选项计算正确．
D、原式，故本选项计算错误．
故选：．
根据合并同类项法则，同底数幂的乘法法则，幂的乘方与积的乘方计算法则以及完全平方公式分别计算．
此题考查了合并同类项法则，同底数幂的乘法法则，幂的乘方与积的乘方计算法则以及完全平方公式，属于基础计算题．
 

6.【答案】 

【解析】解：这组数据数据出现次，次数最多，
所以这组数据的众数为，
第、个数据分别为，，
所以这组数据的中位数为，
故选：．
根据众数和中位数的定义求解即可．
本题主要考查众数和中位数，一组数据中出现次数最多的数据叫做众数．将一组数据按照从小到大或从大到小的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
 

7.【答案】 

【解析】解：根据题意得且，
解得且．
故选：．
利用一元二次方程的定义和判别式的意义得到且得，然后求出两个不等式的公共部分即可．
本题考查了根的判别式：一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．
 

8.【答案】 

【解析】解：由作图得，，
在和中，

≌，
．
故选：．
作图过程可得，，利用判定≌，可得．
本题考查了作图基本作图，解题的关键是掌握全等三角形的判定和性质．
 

9.【答案】 

【解析】解：当时，，即该函数过点，故结论正确，选项A不符合题意；
B.反比例函数，，
在每个象限内，随的增大而增大，故结论错误，选项B符合题意；
C.反比例函数，，
该函数图象为第二、四象限，故结论正确，选项C不符合题意；
D.反比例函数，，
该函数图象为第二、四象限，在每个象限内，随的增大而增大，
当时，，
若，则，故结论正确，选项D不符合题意；
故选：．
把代入可判断；根据反比例函数的性质可判断，，．
本题主要考查了反比例函数的性质，能熟练地根据反比例函数的性质进行判断是解此题的关键．
 

10.【答案】 

【解析】解：更新技术后平均每天比更新技术前多生产万份疫苗，且现在每天生产万份疫苗，
更新技术前每天生产万份疫苗．
依题意得：．
故选：．
根据更新技术前后工作效率间的关系，可得出更新技术前每天生产万份疫苗，利用工作时间工作总量工作效率，结合现在生产万份疫苗所需的时间比更新技术前生产万份疫苗所需时间少用天，即可得出关于的分式方程，此题得解．
本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
 

11.【答案】 

【解析】解：观察图形的变化可知：
第个图形中圆点的个数为；
第个图形中圆点的个数为；
第个图形中圆点的个数为；

发现规律，
则第个图形中圆点的个数为．
故选：．
观察图形的变化可知：第个图形中圆点的个数为；第个图形中圆点的个数为；第个图形中圆点的个数为；进而发现规律，即可得第个图形中圆点的个数．
本题考查了规律型图形的变化类，解决本题的关键是根据图形的变化寻找规律，总结规律．
 

12.【答案】 

【解析】解：过作于，当点在弧上时，扇形的面积最大
，，
，
，
弧的长，
设圆锥的底面圆的半径为，则，解得．
故选：．
根据等腰三角形的性质得到的长，再利用弧长公式计算出弧的长，设圆锥的底面圆的半径为，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到，然后利用勾股定理计算出圆锥的高．
本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
 

13.【答案】 

【解析】解：根据题意得：，解得．
故答案为：．
根据二次根式的定义可知被开方数必须为非负数，列不等式求解．
本题考查的是二次根式有意义的条件，熟知二次根式中的被开方数必须是非负数是解题的关键．
 

14.【答案】 

【解析】解：，
．
即这个多边形的内角和是，
故答案为．
由多边形外角的性质可求解多边形的边数，再利用多边形的内角和定理可求解．
本题主要考查多边形的内角与外角，求解多边形的边数是解题的关键．
 

15.【答案】 

【解析】解：，
故答案为：．
原式提取，再利用完全平方公式分解即可．
此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
 

16.【答案】 

【解析】解：根据旋转过程可知：，，．
．
．
．
过点作于点，
在中，，．
．
在中，
，
．
．

故答案为：．
根据旋转性质及旋转过程可知根据旋转过程可知：，从而得到，，过点作于点，在中，和长，在中可求长，利用即可求解．
本题主要考查了旋转的性质以及特殊直角三角形的性质，解题的关键是作垂线构造直角三角形，利用线段的和差求解即可．
 

17.【答案】解：原式

． 

【解析】直接利用二次根式的性质以及绝对值的性质、零指数幂的性质、负整数指数幂的性质、有理数的乘方运算法则分别化简，进而得出答案．
此题主要考查了实数的运算，正确化简各数是解题关键．
 

18.【答案】证明：，
，
即，
在和中，
，
≌
． 

【解析】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．利用定理证明≌，根据全等三角形的性质证明结论．
 

19.【答案】   

【解析】解：本次调查的样本容量为，
“一般”的人数为人，
补全条形图如下：


故答案为：；
扇形统计图中“较好”对应的扇形圆心角的度数为，
故答案为：；
估计对线上学习评价“非常好”的人数为人．
答：估计对线上学习评价“非常好”的人数人．
由“不好”的人数及其所占百分比可得样本容量；根据各评价的人数之和等于总人数求出“一般”的人数，据此可补全图形；
用乘以“较好”人数所占比例可得；
用总人数乘以样本中学习评价“非常好”的人数所占比例．
本题主要考查了用样本估计总体、扇形统计图、条形统计图的综合应用，解题的关键是明确题意，利用数形结合的思想解答问题．
 

20.【答案】；
根据题意画树状图如下：

共有种等可能的结果数，其中甲组抽到小区，同时乙组抽到小区的结果数为，
甲组抽到小区，同时乙组抽到小区的概率为． 

【解析】解：共有，，，，个小区，
甲组抽到小区的概率是，
故答案为：．
见答案．
直接根据概率公式求解即可；
根据题意画出树状图得出所有等可能的情况数和甲组抽到小区，同时乙组抽到小区的情况数，然后根据概率公式即可得出答案．
此题考查的是树状图法求概率．树状图法适合两步或两步以上完成的事件．用到的知识点为：概率所求情况数与总情况数之比．
 

21.【答案】证明：四边形是平行四边形，
，
，
四边形是平行四边形，
，
，
四边形是矩形；
解：，
，
点为的中点，
，
，
，
四边形是平行四边形，
，
四边形的面积四边形的面积三角形． 

【解析】根据平行四边形的性质得到，推出四边形是平行四边形，根据垂直的定义得到，于是得到结论；
根据直角三角形的性质得到，根据勾股定理得到，根据矩形的周长公式即可得到结论．
本题考查了矩形的判定和性质，平行四边形的性质，勾股定理，正确的识别图形是解题的关键．
 

22.【答案】解：与之间的函数关系式为：；
由题意可得：，
，
，
当时，有最小值元，
此时租车的方案为：型车辆，型车辆． 

【解析】根据题意列出函数解析式即可；
根据一次函数的性质进行解答即可．
本题考查了一次函数的应用，本题难点在于要理清题目中的数量关系，准确找出题目等量关系和不等量关系，列出函数与不等式．
 

23.【答案】解：．
，
点，
将点的坐标代入抛物线表达式：，
解得：，
抛物线的表达式为：；
如图，过点作轴于点，交于点，

，
∽，
，
当：最大时，即：最大，
为定值，
当最大时，：最大，
由、的坐标得：直线的表达式为：，
设点，
则点，
，
当时，最大，
当点时，：最大． 

【解析】由，可知，得点，将点的坐标代入抛物线表达式：并解得：，即可求解；
如图，过点作轴于点，交于点，由，进而可得到∽，进而得到，当：最大时，即：最大，由为定值，所以当最大时，：最大，设点，，，当时，最大，即可得出．
本题主要考查的是待定系数法求二次函数的解析式，二次函数图象上点的坐标特征，二次函数的最值，三角形相似的判定和性质，求得的长是解题的关键．
 

24.【答案】解：如图，连接、，
当时，与相切，
是的直径，
，
，
，
，
是的切线，
，
，
，，
，
，
，
，
解得，
当时，与相切．
存在为等腰三角形，
，，，
，
，，
当时，如图，作于点，则，
，
，
解得；
当时，如图，则，
解得；
当时，如图，作于点，则，，
，
，
，
解得，
综上所述，存在为等腰三角形，的值为或或． 

【解析】连接、，当时，与相切，可证明是的切线，则，所以，则，，得，则，所以，则，得，所以当时，与相切；
由，，，得，则，，再分三种情况讨论，一是当时，作于点，则，于是得，则；二是当时，则，得；三是当时，作于点，则，，，于是得，则．
此题重点考查切线的判定与性质、切线长定理、勾股定理、锐角三角函数与解直角三角形、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性较强，难度较大，正确地作出所需要的辅助线是解题的关键．