

2022-2023学年江西省南昌市青云谱区江铃学校九年级(下)月考数学试卷(4月份)(含解析)
展开2022-2023学年江西省南昌市青云谱区江铃学校九年级(下)月考数学试卷(4月份)
一、选择题(共6小题,共18分)
1.计算|﹣2|的结果为( )
A.2 B.﹣2 C.﹣ D.
2.下列运算正确的是( )
A.(﹣a3)2=﹣a6 B.2a2+3a2=6a2
C.2a2•a3=2a6 D.
3.如图,该几何体的左视图是( )
A. B. C. D.
4.如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. B. C. D.
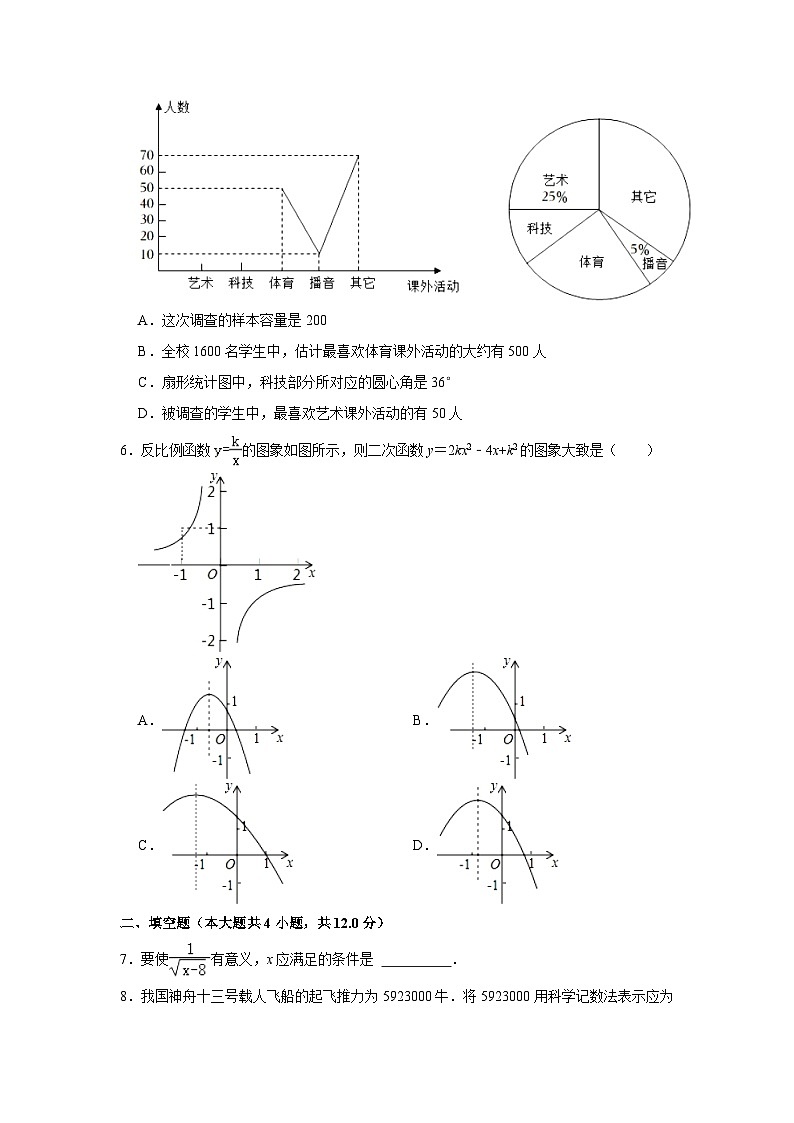
5.某中学对学生最喜欢的课外活动进行了随机抽样调查,要求每人只能选择其中的一项.根据得到的数据,绘制的不完整统计图如下,则下列说法中不正确的是( )
A.这次调查的样本容量是200
B.全校1600名学生中,估计最喜欢体育课外活动的大约有500人
C.扇形统计图中,科技部分所对应的圆心角是36°
D.被调查的学生中,最喜欢艺术课外活动的有50人
6.反比例函数的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
A. B.
C. D.
二、填空题(本大题共4小题,共12.0分)
7.要使有意义,x应满足的条件是 .
8.我国神舟十三号载人飞船的起飞推力为5923000牛.将5923000用科学记数法表示应为 .
9.非零实数m,n(m≠n)满足m2﹣m﹣2=0,n2﹣n﹣2=0,则= .
10.如图,点A是直线y=﹣2x+3上的动点,过点A作AB垂直x轴于点B,y轴上存在点C,能使以A、B、C为顶点的三角形是等腰直角三角形.请写出所有符合条件的点C的坐标 .
三、计算题(本大题共2小题,共14.0分)
11.解不等式组,并在数轴上表示解集,
12.某地新茶上市,一茶商在该地收购新茶,茶商经过包装处理试销数日发现,平均每斤茶叶利润为20元,并且每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤.设销售单价每增加x元,每天售出y斤.
(1)求y与x的函数关系式;
(2)求该茶商每天的最大利润.
四、解答题(本大题共9小题,共76.0分。解答应写出文字说明,证明过程或演算步骤)
13.某校八年级计划在开学第二周的星期二至星期五开展社会实践活动,要求每位学生选择两天参加活动.
(1)乙同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)甲同学随机选择两天.请用列表或画树状图的方法求其中有一天是星期三的概率.
14.在△ABC中,AB=AC,点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦EF,使EF∥BC;
(2)在图2中作出圆心O.
15.如图,在△ABC中,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE.
(1)求证:四边形ADCF是平行四边形.
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
16.如图,某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.7米的学生进入识别区域时,在点B处测得摄像头M的仰角为30°,在点C处测得摄像头M的仰角为60°,求学校大门ME的高是多少米.
17.为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“B”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
18.如图,一次函数y=kx+b与反比例函数y=图象交于A,B两点,与x轴交于点C(﹣2,0),点A的横坐标为1,S△AOC=2.
(1)求一次函数及反比例函数的表达式;
(2)直接写出反比例函数值大于一次函数值时x的取值范围.
19.如图,已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC,交⊙O于点D,交AC于点E,连接BD,BD交AC于点F,延长AC到点P,连接PB.
(1)若PF=PB,求证:PB是⊙O的切线;
(2)如果AB=10,BC=6,求CE的长度.
20.如图,已知A(3,0),B(0,﹣1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;
(3)在(2)的条件下若C、P,Q三点共线,求此时∠APB的度数及P点坐标.
21.如图,在平面直角坐标系xOy中,抛物线y=x2+ax+a﹣5与x轴交于点A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=﹣1.
(1)求抛物线的解析式及顶点坐标;
(2)若P(n,c)和Q(2,b)是抛物线上两点,且c<b,求n的取值范围;
(3)连接BC,若M(xM,yM)是y轴左侧抛物线上的一点,N为x轴上一动点,当MN∥BC,且MN>BC时,请直接写出点M的横坐标xM的取值范围.
参考答案
一、选择题(本大题共6小题,共18.0分。在每小题列出的选项中,选出符合题目的一项)
1.计算|﹣2|的结果为( )
A.2 B.﹣2 C.﹣ D.
【分析】利用绝对值的定义即可求解.
解:|﹣2|=2.
故选:A.
【点评】此题主要考查了绝对值的定义,比较简单.
2.下列运算正确的是( )
A.(﹣a3)2=﹣a6 B.2a2+3a2=6a2
C.2a2•a3=2a6 D.
【分析】分别根据幂的乘方、合并同类项法则、同底数幂的乘法及分式的乘方逐一计算即可判断.
解:A、(﹣a3)2=a6,此选项不合题意;
B、2a2+3a2=5a2,此选项不合题意;
C、2a2•a3=2a5,此选项不合题意;
D、,此选项符合题意.
故选:D.
【点评】本题主要考查整式的运算,解题的关键是掌握幂的乘方、合并同类项法则、同底数幂的乘法及分式的乘方的运算法则.
3.如图,该几何体的左视图是( )
A. B. C. D.
【分析】根据左视图是从左边看,得出结论即可.
解:由题意知,原几何体的左视图为一个矩形,矩形的内部有一条横向的虚线.
故选:D.
【点评】本题主要考查简单组合体的三视图,熟练掌握三视图的知识是解题的关键.
4.如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
A. B. C. D.
【分析】根据轴对称图形的性质得,将序号②④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形,再利用概率公式进行计算即可.
解:根据轴对称图形的性质得,将序号②④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形,
∴与图中阴影部分构成轴对称图形的概率是=,
故选:B.
【点评】本题主要考查了轴对称图形的性质,概率公式等知识,熟练掌握轴对称图形的性质是解题的关键.
5.某中学对学生最喜欢的课外活动进行了随机抽样调查,要求每人只能选择其中的一项.根据得到的数据,绘制的不完整统计图如下,则下列说法中不正确的是( )
A.这次调查的样本容量是200
B.全校1600名学生中,估计最喜欢体育课外活动的大约有500人
C.扇形统计图中,科技部分所对应的圆心角是36°
D.被调查的学生中,最喜欢艺术课外活动的有50人
【分析】根据统计图分别判断各个选项即可.
解:∵10÷5%=200,
∴这次调查的样本容量为200,
故A选项结论正确,不符合题意;
∵1600×=400(人),
∴全校1600名学生中,估计最喜欢体育课外活动的大约有400人,
故B选项结论不正确,符合题意;
∵200×25%=50(人),
∴被调查的学生中,最喜欢艺术课外活动的有50人,
故D选项结论正确,不符合题意;
∵360°×=36°,
∴扇形统计图中,科技部分所对应的圆心角是36°,
故C选项结论正确,不符合题意;
故选:B.
【点评】本题主要考查统计的知识,熟练掌握扇形统计图等统计的知识是解题的关键.
6.反比例函数的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
A. B.
C. D.
【分析】本题可先由反比例函数的图象得到字母系数k>﹣1,再与二次函数的图象的开口方向和对称轴的位置相比较看是否一致,最终得到答案.
解:∵函数y=的图象经过二、四象限,
∴k<0,
由图知当x=﹣1时,y=﹣k<1,
∴k>﹣1,
∴抛物线y=2kx2﹣4x+k2开口向下,
对称轴为x=﹣=,<﹣1,
∴对称轴在直线x=﹣1的左边.
∴当x=0时,y=k2<1.
故选:B.
【点评】此题主要考查了二次函数与反比例函数的图象与系数的综合应用,正确判断抛物线开口方向和对称轴位置是解题关键.属于基础题.
二、填空题(本大题共4小题,共12.0分)
7.要使有意义,x应满足的条件是 x>8 .
【分析】根据二次根式(a≥0)以及分母不为0可得:x﹣8>0,然后进行计算即可解答.
解:由题意得:
x﹣8>0,
解得:x>8,
故答案为:x>8.
【点评】本题考查了二次根式有意义的条件,分式有意义的条件,熟练掌握二次根式(a≥0)以及分母不为0是解题的关键.
8.我国神舟十三号载人飞船的起飞推力为5923000牛.将5923000用科学记数法表示应为 5.923×106 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:5923000=5.923×106.
故答案为:5.923×106.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
9.非零实数m,n(m≠n)满足m2﹣m﹣2=0,n2﹣n﹣2=0,则= .
【分析】根据已知判断出m,n是方程x2﹣x﹣2=0的两实数根,然后利用根与系数关系即可求解.
解:∵实数m,n(m≠n)满足等式m2﹣m﹣2=0,n2﹣n﹣2=0,
∴m,n是方程x2﹣x﹣2=0的两实数根,
∴m+n=1,mn=﹣2,
∴,
故答案为:.
【点评】本题考查一元二次方程的根与系数关系,能熟练利用方程解的定义得到m,n是方程x2﹣x﹣2=0的两实数根是解题的关键.
10.如图,点A是直线y=﹣2x+3上的动点,过点A作AB垂直x轴于点B,y轴上存在点C,能使以A、B、C为顶点的三角形是等腰直角三角形.请写出所有符合条件的点C的坐标 (0,1)、(0,0)、(0,﹣3)、(0,) .
【分析】等腰直角三角形可以以A、B、C任意一个为直角顶点,所以分三种情况讨论.以A为直角顶点时AB=AC,以B为直角顶点时,由于AB⊥x轴,所以C点为原点,以C为顶点时,AC=BC,因A在直线上,AB⊥x轴,C在y轴,可列方程求得C点的坐标.
解:以A、B、C为顶点的等腰直角三角形分为以A为直角顶点,以B为直角顶点,以C为直角顶点三种情况.
设A(x,y),B(x,0),C(0,c),
(1)以A为直角顶点,则AB、AC为等腰的两条边,
∴若y=x=c.
由A在直线y=﹣2x+3得:x=﹣2x+3
∴x=1,y=1故得C(0,1).
若y=﹣x=c的情况,
∴﹣x=﹣2x+3,解得x=3,
C的坐标为(0,﹣3)
(2)以B为直角,则AB,BC为等腰的两条边,
∴C(0,0).
(3)以C为直角,则AC,BC为等腰的两条边,
此时y2=2×(x2+c2),(y﹣c)2+x2=x2+c2,
又y=﹣2x+3,
∴联立解得:c=
故得C(0,).
综上所述:C的所有可能值为(0,1)(0,0)(0,﹣3)(0,).
【点评】本题考查的是思维的紧密性及直线和等腰直角三角形的有关知识,考虑问题一定要全面,分类讨论.
三、计算题(本大题共2小题,共14.0分)
11.解不等式组,并在数轴上表示解集,
【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解:,
解不等式①得:x≥﹣1,
解不等式②得:x<2,
∴不等式组的解集为﹣1≤x<2,
数轴表示如图:.
【点评】本题考查解一元一次不等式组,解题关键是准确求解每个不等式.
12.某地新茶上市,一茶商在该地收购新茶,茶商经过包装处理试销数日发现,平均每斤茶叶利润为20元,并且每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤.设销售单价每增加x元,每天售出y斤.
(1)求y与x的函数关系式;
(2)求该茶商每天的最大利润.
【分析】(1)根据“每天可售出60斤.进一步根据茶叶市场调查发现,销售单价每增加5元,每天销售量会减少10斤”列函数关系式即可;
(2)根据每天的利润=每斤的利润×销售量列出函数解析式,根据函数的性质求出函数最值.
解:(1)根据题意得,y=60﹣2x;
(2)设茶商每天的利润为w元,根据题意得,w=(20+x)(﹣2x+60)=﹣2(x﹣5)2+1250,
∵a=﹣2<0,
∴当x=5时,w最大=1250元,
答:该茶商每天的最大利润为1250元.
【点评】本题考查了二次函数的应用,弄清题目中包含的数量关系是解题关键.
四、解答题(本大题共9小题,共76.0分。解答应写出文字说明,证明过程或演算步骤)
13.某校八年级计划在开学第二周的星期二至星期五开展社会实践活动,要求每位学生选择两天参加活动.
(1)乙同学随机选择连续的两天,其中有一天是星期三的概率是 ;
(2)甲同学随机选择两天.请用列表或画树状图的方法求其中有一天是星期三的概率.
【分析】(1)由题意得,乙同学随机选择连续的两天可能出现结果有3种,其中有一天是星期三的结果有2种,根据概率公式可得答案.
(2)列表得出所有等可能的结果,以及甲同学随机选择两天,其中有一天是星期三的结果,再利用概率公式可得出答案.
解:(1)由题意得,乙同学随机选择连续的两天可能出现结果有:(星期二,星期三),(星期三,星期四),(星期四,星期五),共3种,
其中有一天是星期三的结果有2种,
∴其中有一天是星期三的概率是.
故答案为:.
(2)列表如下:
星期二
星期三
星期四
星期五
星期二
(星期二,星期三)
(星期二,星期四)
(星期二,星期五)
星期三
(星期三,星期二)
(星期三,星期四)
(星期三,星期五)
星期四
(星期四,星期二)
(星期四,星期三)
(星期四,星期五)
星期五
(星期五,星期二)
(星期五,星期三)
(星期五,星期四)
共有12种等可能的结果,其中有一天是星期三的结果有6种,
∴甲同学随机选择两天,其中有一天是星期三的概率为=.
【点评】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
14.在△ABC中,AB=AC,点A在以BC为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦EF,使EF∥BC;
(2)在图2中作出圆心O.
【分析】(1)延长BA、CA分别交半圆于F、E,利用圆周角定理得到∠E=∠B=∠C=∠F,则EF∥BC;
(2)延长BE、CF交于G,连接GA并延长与直径交点即为圆心.
解:(1)如图,EF为所作;
(2)如图,点O为所作.
【点评】本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的性质和圆周角定理.
15.如图,在△ABC中,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE.
(1)求证:四边形ADCF是平行四边形.
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
【分析】(1)利用旋转的性质得出点A、E、C三点共线,点D、E、F三点共线,且AE=CD,DE=FE,即可得出答案;
(2)首先得出CD⊥AB,即∠ADC=90°,由(1)知,四边形ADCF是平行四边形,故四边形ADCF是矩形.进而求出CD=AD即可得出答案.
【解答】(1)证明:∵△CFE是由△ADE绕点E旋转180°得到,
∴点A、E、C三点共线,点D、E、F三点共线,
且AE=CE,DE=FE,
故四边形ADCF是平行四边形.
(2)解:当∠ACB=90°,AC=BC时,四边形ADCF是正方形.
理由如下:
在△ABC中,∵AC=BC,AD=BD,
∴CD⊥AB,即∠ADC=90°.
而由(1)知,四边形ADCF是平行四边形,
∴四边形ADCF是矩形.
又∵∠ACB=90°,
∴,
故四边形ADCF是正方形.
【点评】此题主要考查了平行四边形的判定以及正方形的判定等知识,得出四边形ADCF是矩形是解题关键.
16.如图,某学校门口安装了体温监测仪器,体温检测有效识别区域AB长为6米,当身高为1.7米的学生进入识别区域时,在点B处测得摄像头M的仰角为30°,在点C处测得摄像头M的仰角为60°,求学校大门ME的高是多少米.
【分析】根据题意得:AC=BD=EF=1.7米,AB=CD=6米,∠MFD=90°,再利用三角形的外角性质可得∠CDM=∠CMD=30°,从而可得CD=CM=6米,然后在Rt△MCF中,利用锐角三角函数的定义求出MF的长,最后利用线段的和差关系,进行计算即可解答.
解:由题意得:
AC=BD=EF=1.7米,AB=CD=6米,∠MFD=90°,
∵∠MCF是△MCD的一个外角,
∴∠MCF=∠CDM+∠CMD,
∴∠CMD=∠MCF﹣∠CDM=30°,
∴∠CDM=∠CMD=30°,
∴CD=CM=6米,
在Rt△MCF中,MF=MC•sin60°=6×=3(米),
∴ME=MF+EF=(1.7+3)米,
∴学校大门ME的高是(1.7+3)米.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
17.为了响应市政府号召,某校开展了“六城同创与我同行”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 60 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“B”所在扇形的圆心角等于 108 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式求他们恰好选中同一个主题活动的概率.
【分析】(1)用“A”的频数除以所占比例即可得出答案;
(2)求出“C”的频数,补全条形统计图即可;
(3)用360°乘以“B”所占的比例即可;
(4)画出树状图,由概率公式即可得出结果.
解:(1)本次随机调查的学生人数=15÷25%=60人;
故答案为:60;
(2)60﹣15﹣18﹣9=18(人),补全条形统计图如图1所示:
(3)在扇形统计图中,“B”所在扇形的圆心角=360°×=108°,
故答案为:108;
(4)画树状图如图2所示:
共有16个等可能的结果,
小明和小华恰好选中同一个主题活动的结果有4个,
∴小明和小华恰好选中同一个主题活动的概率==.
【点评】本题考查了列表法与树状图法、扇形统计图、条形统计图;读懂题意,画出树状图是解题的关键.
18.如图,一次函数y=kx+b与反比例函数y=图象交于A,B两点,与x轴交于点C(﹣2,0),点A的横坐标为1,S△AOC=2.
(1)求一次函数及反比例函数的表达式;
(2)直接写出反比例函数值大于一次函数值时x的取值范围.
【分析】(1)根据C的坐标和S△AOC=2求得A的坐标,然后根据待定系数法即可求得一次函数及反比例函数的表达式;
(2)联立方程求得B的坐标,根据图象即可求得.
解:(1)∵C(﹣2,0),S△AOC=2.
∴OC=2,OC•|yA|=2,
∴|yA|=2,
∵点A在第一象限,
∴A(1,2),
∵A点在反比例函数y=图象上,
∴m=1×2=2,
∵一次函数y=kx+b经过A(1,2),C(﹣2,0),
∴,解得,
∴一次函数的解析式为y=x+,反比例函数的解析式为y=;
(2)∵解得或,
∴B(﹣3,﹣),
∴反比例函数值大于一次函数值时x的取值范围:x<﹣3或0<x<1.
【点评】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数的解析式.也考查了三角形面积公式、待定系数法求函数的解析式.
19.如图,已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC,交⊙O于点D,交AC于点E,连接BD,BD交AC于点F,延长AC到点P,连接PB.
(1)若PF=PB,求证:PB是⊙O的切线;
(2)如果AB=10,BC=6,求CE的长度.
【分析】(1)根据等边对等角以及对顶角相等可以证得∠DFE=∠PBF,∠D=∠DBO,然后根据圆周角定理证明△DEF是直角三角形,据此即可证得∠PBA=90°,从而证明PB是切线;
(2)根据三角形的中位线定理求得OE的长,然后根据垂径定理即可求解.
【解答】(1)证明:∵PF=PB,
∴∠PFB=∠PBF,
又∵∠DFE=∠PFB,
∴∠DFE=∠PBF,
∵AB是圆的直径,
∴∠ACB=90°,即AC⊥BC.
又∵OD∥BC,
∴OD⊥AC.
∴在直角△DEF中,∠D+∠DFE=90°,
又∵OD=OB,
∴∠D=∠DBO,
∴∠DBO+∠PBE=90°,即PB⊥AB,
∴PB是⊙O的切线;
(2)解:∵OD∥BC,OA=OB,
∴OE=BC=×6=3.
∵OD⊥AB,
∴EC=AE.
∵在直角△OAE中,OA=AB=×10=5,
∴AE===4.
∴EC=4.
【点评】本题考查了圆周角定理、垂径定理以及等边对等角的性质,本题中证明OD⊥AC是关键.
20.如图,已知A(3,0),B(0,﹣1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;
(3)在(2)的条件下若C、P,Q三点共线,求此时∠APB的度数及P点坐标.
【分析】(1)作CH⊥y轴于H,证明△ABO≌△BCH,根据全等三角形的性质得到BH=OA=3,CH=OB=1,求出OH,得到C点坐标;
(2)证明△PBA≌△QBC,根据全等三角形的性质得到PA=CQ;
(3)根据C、P,Q三点共线,得到∠BQC=135°,根据全等三角形的性质得到∠BPA=∠BQC=135°,根据等腰三角形的性质求出OP,得到P点坐标.
解:(1)作CH⊥y轴于H,
则∠BCH+∠CBH=90°,
∵AB⊥BC,
∴∠ABO+∠CBH=90°,
∴∠ABO=∠BCH,
在△ABO和△BCH中,
,
∴△ABO≌△BCH,
∴BH=OA=3,CH=OB=1,
∴OH=OB+BH=4,
∴C点坐标为(1,﹣4);
(2)∵∠PBQ=∠ABC=90°,
∴∠PBQ﹣∠ABQ=∠ABC﹣∠ABQ,即∠PBA=∠QBC,
在△PBA和△QBC中,
,
∴△PBA≌△QBC,
∴PA=CQ;
(3)∵△BPQ是等腰直角三角形,
∴∠BQP=45°,
当C、P,Q三点共线时,∠BQC=135°,
由(2)可知,△PBA≌△QBC,
∴∠BPA=∠BQC=135°,
∴∠OPB=45°,
∴OP=OB=1,
∴P点坐标为(1,0).
【点评】本题考查的是全等三角形的判定和性质、三角形的外角的性质,掌握全等三角形的判定定理和性质定理是解题的关键.
21.如图,在平面直角坐标系xOy中,抛物线y=x2+ax+a﹣5与x轴交于点A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=﹣1.
(1)求抛物线的解析式及顶点坐标;
(2)若P(n,c)和Q(2,b)是抛物线上两点,且c<b,求n的取值范围;
(3)连接BC,若M(xM,yM)是y轴左侧抛物线上的一点,N为x轴上一动点,当MN∥BC,且MN>BC时,请直接写出点M的横坐标xM的取值范围.
【分析】(1)根据对称轴求出a的值,即可求函数的解析式;
(2)抛物线开口向上,图象上的点离对称轴越远对应的函数值越大,由此可得|n+1|<3,求出n的范围即可;
(3)求出直线MN的解析式,确定N点坐标,再由MN>BC,可得+2xM﹣3|>3,求出xM的取值范围即可.
解:(1)∵对称轴是直线x=﹣1,
∴﹣=﹣1,
解得a=2,
∴y=x2+2x﹣3,
∴顶点坐标为(﹣1,﹣4);
(2)∵P(n,c)和Q(2,b)是抛物线上两点,且c<b,
∴|n+1|<3,
解得﹣4<n<2;
(3)令x=0,则y=﹣3,
∴C(0,﹣3),
令y=0,则x2+2x﹣3=0,
解得x=﹣3或x=1,
∴B(1,0),A(﹣3,0),
设直线BC的解析式为y=kx+b,
∴,
解得,
∴y=3x﹣3,
∵MN∥BC,
∴直线MN的解析式为y=3x+yM﹣3xM,
∴N(xM﹣yM,0),
∵MN>BC,
∴|yM|>,
∴|yM|>3,
∵yM=+2xM﹣3,
∴+2xM﹣3|>3,
解得﹣2<xM<0或xM<﹣1﹣.
【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,两直线平行k值相等,绝对值不等式的解法是解题的关键.
2022-2023学年江西省南昌市青云谱区民德学校八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年江西省南昌市青云谱区民德学校八年级(下)期末数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江西省南昌市青云谱区重点学校八年级(下)期末数学试卷: 这是一份2022-2023学年江西省南昌市青云谱区重点学校八年级(下)期末数学试卷,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江西省南昌市青云谱区重点学校九年级(下)月考数学试卷(4月份)-普通用卷: 这是一份2022-2023学年江西省南昌市青云谱区重点学校九年级(下)月考数学试卷(4月份)-普通用卷,共20页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












