（浙江杭州卷）2023年中考数学第三次模拟考试

这是一份（浙江杭州卷）2023年中考数学第三次模拟考试，文件包含浙江杭州卷2023年中考数学第三次模拟考试全解全析docx、浙江杭州卷2023年中考数学第三次模拟考试参考答案docx、浙江杭州卷2023年中考数学第三次模拟考试A4考试版docx、浙江杭州卷2023年中考数学第三次模拟考试答题卡pdf、浙江杭州卷2023年中考数学第三次模拟考试考试版docx等5份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。
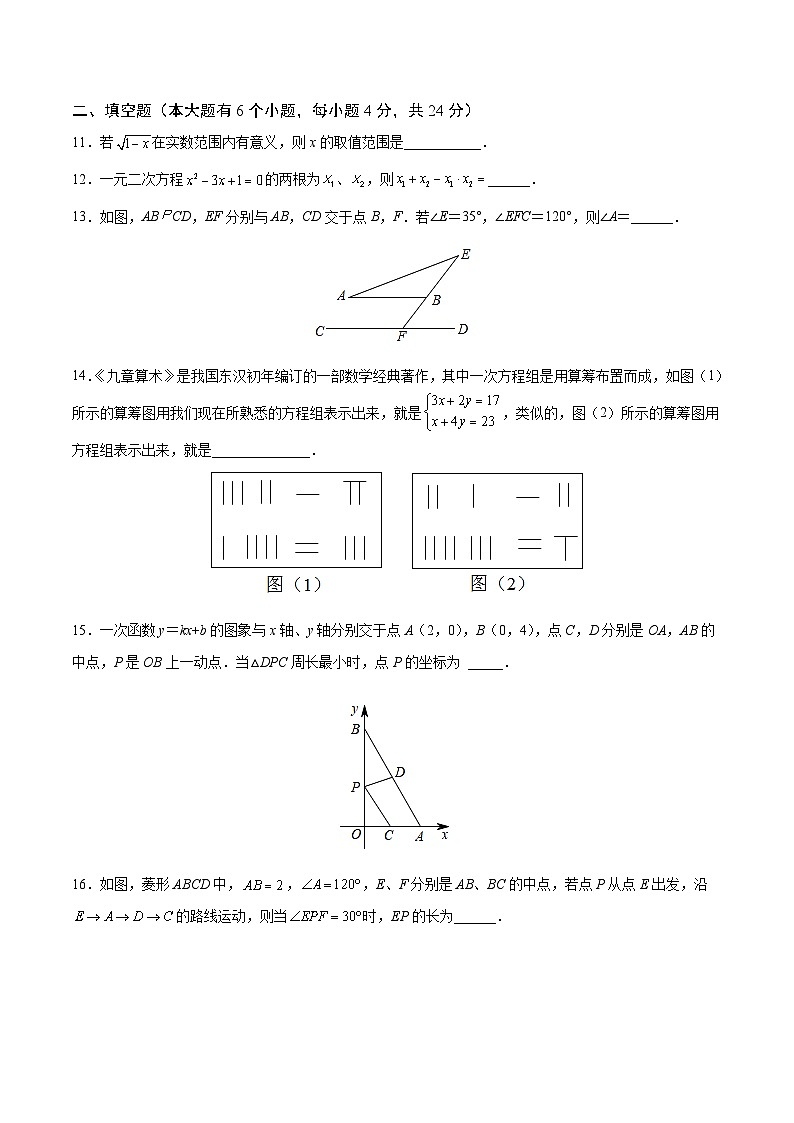
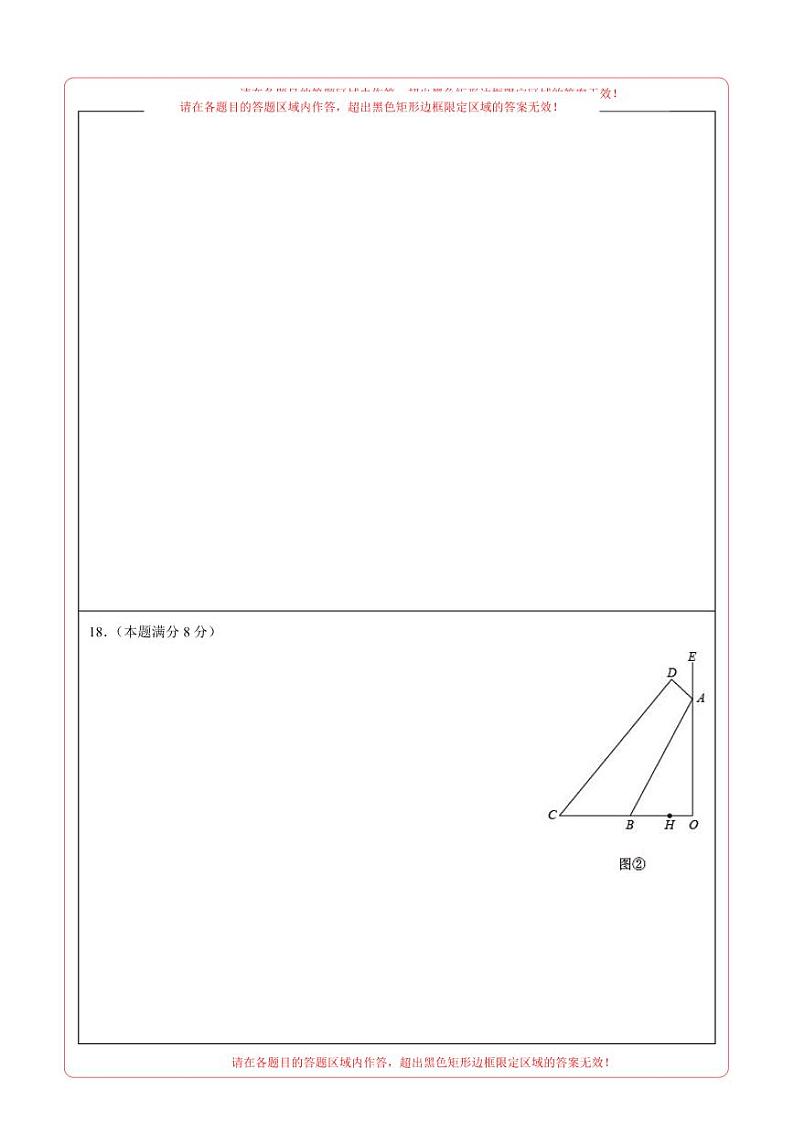
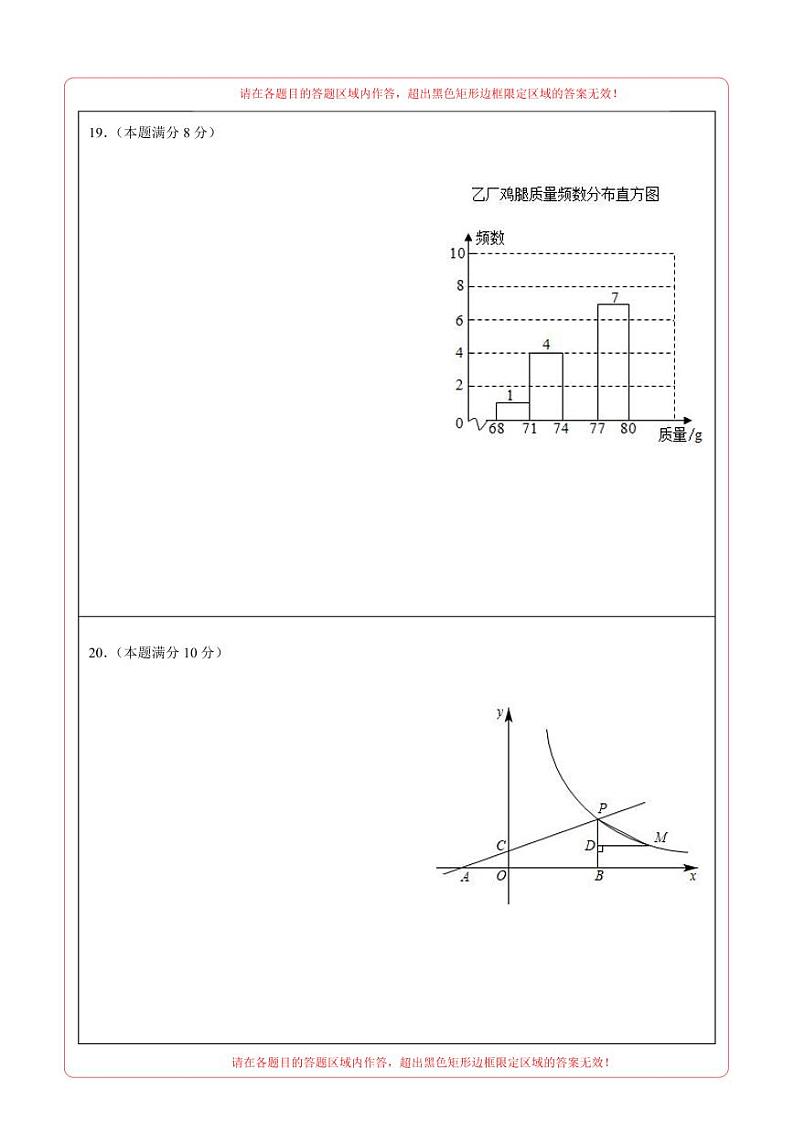
2023年中考数学第三次模拟考试【浙江杭州卷】数学·参考答案一、选择题12345678910BCABBBCCDD二、填空题11．                            12．2                       13．25°14．                    15．（0，1）                  16．1或或2三、解答题17．（1），1；（2）1，2，3，4【解析】【分析】（1）先对原式化简，然后将代入化简后的式子即可解答本题；（2）先求出不等式组的解集，再找到其正整数解即可．【详解】解：（1），当时，原式；（2） 解①得：，解②得：，∴原不等式组的解集为：∴该不等式组的正整数解为：1，2，3，4．【点睛】本题考查分式的化简求值和一元一次不等式组的解集，解题的关键是明确它们各自的计算方法．18．(1)点D到OE的距离约为0.6米(2)OA的长约是4米【解析】【分析】（1）过D作DF⊥AE于F， 在直角三角形中，通过解三角函数即可求解；（2）分别用OC=CH+OH=O.8+AO+0.6，OC=BC+OB=2.4+，列出等式，求出OA即可．(1)解：过D作DF⊥AE于F，  ∵AD=1，DF⊥AE∴点D到OE的距离约为0.6米(2)过D作DH⊥OC于H，则四边形AHCF是矩形， 在Rt△AOB中，∠ABO=53°∴∠BAO=37°，∴∵从C处沿C0方向走4步到达点B处，，已知现测学生的步长为0.6米.∴BC=2.4米∴OC=BC+OB=2.4+∵AD=1，DF⊥AE∴∵∠DCO=45°∴CH=DH=OF=0.8+AO∵四边形DHOF是矩形∴OH=DF=0.6∴OC=CH+OH=O.8+AO+0.6∴2.4+=O.8+AO+0.6∴AO=4MI米答：匾额悬挂的高度是4米．【点睛】本题考查了解直角三角形的应用-仰角俯角问题，解答本题的关键是根据仰角构造直角三角形，利用三角函数求解．19．(1)0.5，76(2)见解析(3)见解析(4)13000只【解析】【分析】（1）根据频数、频率、总数之间的关系可求出a的值，根据众数的意义可求出b的值；（2）求出乙厂鸡腿质量在74≤x＜77的频数，即可补全频数分布直方图；（3）根据方差进行判断即可；（4）求出甲厂鸡腿质量在71≤x＜77的鸡腿数量所占的百分比即可．(1)a＝10÷20＝0.5，甲厂鸡腿质量出现次数最多的是76g，因此众数是76，即b＝76，故答案为：0.5，76；(2)20﹣1﹣4﹣7＝8（只），补全频数分布直方图如下：(3)两个厂的平均数相同，都是75g，而要求的规格是75g，由于甲厂的方差较小，数据比较稳定，因此选择甲厂；(4)20000×（0.15＋0.5）＝13000（只），答：从甲厂采购了20000只鸡腿中，可以加工成优等品的大约有13000只．【点睛】本题考查了频数分布表、频数分布直方图、方差、众数、平均数等，掌握频数、频率、总数之间的关系是解题的关键．20．(1)(2)(8，)【解析】【分析】（1）将点P的纵坐标代入一次函数解析式可求出其横坐标，即得出点P坐标．再将点P坐标代入反比例函数解析式即可求出m的值；（2）利用分类讨论的思想，根据正切的定义结合图形，建立等式求解即可．(1)∵点P纵坐标为4，且在一次函数图象上，∴4=x+1，解得x=3，∴P(3，4)．又∵点P在反比例函数图象上，∴，解得；(2)∵，∴．设PD=t(t>0)，则DM=2t，分类讨论①当M点在P点右侧时，如图，∴M点的坐标为(3+2t，4−t)，∴，解得：(舍)∴，．∴此时M点的坐标为(8，)；②当M点在P点的左侧时，∴M点的坐标为(3−2t，4+t)，∴，解得：(均舍去)．故此情况不合题意．综上，M点的坐标为(8，)．【点睛】本题考查了一次函数与反比例函数的交点问题，反比例函数解析式的确定，三角函数，一元二次方程的解法．熟练掌握函数图象交点的意义，灵活运用三角函数的定义，构造一元二次方程并准确解答是解题的关键．21．(1)见解析；(2)；(3)或；【解析】【分析】（1）利用角平分线的定义和圆周角定理求得∠ODB=45°，即可证明；（2）连接OD，设CD、AB交于点F，作FM⊥AC于M，FN⊥BC于N，利用角平分线的性质结合面积关系求出AF∶BF=4∶3，由AB的长可得OF的长；再由勾股定理求出DF的长，解直角三角形即可解答；（3）连接OD，作BF⊥DE于F，设BE=5k，CB=4k，则CE=9k；由△DEB∽△CED，求出DE的长；Rt△BEF中，利用勾股定理列方程得出BF的长，再由四边形ODFB是正方形可得AB的长，进而求出AC的长即可解答；(1)解：如图，连接OD， ∵AB为圆的直径，∴∠ACB=90°，∵CD平分∠ACB，∴∠ABD=∠ACD=45°，∠AOD=∠BOD=90°；∴∠ODB=90°-45°=45°，∵∠BDE=45°，∴∠ODE=90°，∴DE是圆的切线；(2)解：连接OD，设CD、AB交于点F，作FM⊥AC于M，FN⊥BC于N，OH⊥CD于H， Rt△ABC中，由勾股定理可得BC=，由角平分线的性质可得FM=FN，∴△ACF面积∶△BCF面积=8∶6=4∶3，∴AF∶BF=4∶3，∵AB=10，∴AF=，BF=，∴OF=，∵∠BDE=∠ABD=45°，∴AB∥DE，∵OD⊥DE，∴DO⊥AB，Rt△ODF中，DF==，∴sin∠ODF==，∴OH=ODsin∠ODH=；(3)解：连接OD，作BF⊥DE于F， ，设BE=5k，CB=4k，则CE=9k，∵∠BDE= ∠DCE=45°，∠DEB= ∠CED，∴△DEB∽△CED，∴，DE=，设BF=x，∵OD⊥DE，OD⊥AB，BF⊥DE，OD=OB，∴四边形ODFB是正方形，∴DF=BF=x，EF=-x，Rt△BEF中，BE2=BF2+EF2，∴25k2=x2+45k2+x2-x解得：x=或x=； x=时，AB= 2x=，BC=4k，AC=，tan∠AEC==；x=时，AB= 2x=，BC=4k，AC=，tan∠AEC==；∴tan∠AEC的值为：或；【点睛】本题考查了圆周角定理，切线的性质，角平分线的性质，比例的性质，解直角三角形，相似三角形的判定和性质，综合性强难度大；根据相关性质作辅助线是解题关键．22．(1)见解析；(2)AE＝CF，证明见解析；(3)5【解析】【分析】（1）证明△DAE≌△DCF（ASA），可得结论；（2）证明△DAE≌△DCF（ASA），可得结论；（3）如图4中，连接AC，取AC的中点O，连接OE，OD．证明∠AED＝∠DEC＝45°，AE＝AF，勾股定理求得EF，由DF＝3，得到答案(1)证明：如图1中，∵四边形ABCD是正方形，∴DA＝DC，∠A＝∠ADC＝∠DCB＝∠DCF＝90°，∵DE⊥DF，∴∠EDF＝∠ADC＝90°，∴∠ADE＝∠CDF，在△DAE和△DCF中，，∴△DAE≌△DCF（ASA），∴AE＝CF．(2)解：AE＝CF理由如下：如图2中，∵四边形ABCD是正方形，∴DA＝DC，∠DAB＝∠ADC＝∠DCB＝90°，∵DE⊥DF，∴∠EDF＝∠ADC＝90°，∴∠ADE＝∠CDF，∵AE⊥EF，∴∠AEF＝90°，∴∠DAE+∠DCE＝360°－∠AEF－∠ADC＝180°，∵∠DCF+∠DCE＝180°，∴∠DAE＝∠DCF，在△DAE和△DCF中， ∴△DAE≌△DCF（ASA），∴AE＝CF．(3)解：如图4中，连接AC，取AC的中点O，连接OE，OD． ∵四边形ABCD是正方形，∴OA＝OC＝AC＝BD＝OD，∠ADC＝90°，∠ACD＝45°，AD＝CD∵AE⊥EC，∴∠AEC＝∠ADC＝90°，∴ △AEC是直角三角形∴OE＝AC，∴OD＝OA＝OC＝OE∴A，E，C，D四点共圆，∴∠AED＝∠ACD＝45°，∴∠AED＝∠DEC＝45°，∵AE⊥AF，∴∠EAF＝90°，∴∠AEF＝∠AFE＝45°，∴AE＝AF＝，∴EF＝＝2，∵DF＝3，∴DE＝EF +DF＝5，【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，四点共圆，圆周角定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用建模的思想思考问题，属于中考常考题．23．(1)，(2)①；②见解析(3)【解析】【分析】（1）根据二次函数与一次函数的交点的求法列出一元二次方程求解即可；（2）因为、两点都是伴随直线上的点，所以可以利用待定系数法求出伴随直线的解析式，即可得到伴随点的坐标；然后根据计算结果画出伴随直线即可；（3）分两种情况讨论根据题意求出的值，然后证明，即可求出的值，从而可以确定抛物线的解析式．(1)解：抛物线的伴随直线是，由得，解得，，当时，；当时，，，；(2)解：①把点，代入伴随直线得，解得，伴随点；②所画图形如图所示：(3)解：如图，若，伴随直线：与轴交于点，则，又，，，又，四边形为平行四边形，，若，，即，，，，，即，，抛物线；如图，若，伴随直线：与轴交于点，则，又，，，又，四边形为平行四边形，，若，，即，，，，，即，，抛物线，综上可知，所求抛物线是或．【点睛】本题考查待定系数法求一次函数的解析式、二次函数的性质、二次函数与一元二次方程的关系，本题综合性比较强．